Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
Main>Walla Marina K (Die Seite wurde neu angelegt: = <span style="color: green">Aufstellen und Interpretieren von Termen</span> = ==<span style="color: green">Aufstellen von Termen </span> == <div style="margin:0px; m...) |
Keine Bearbeitungszusammenfassung |
||
| (47 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Lernpfad Terme}}|Lernschritte einblenden|Lernschritte ausblenden}} | |||
__NOTOC__ | |||
=Aufstellen und Interpretieren von Termen= | |||
==Aufstellen von Termen== | |||
===Aufgabenstellung=== | |||
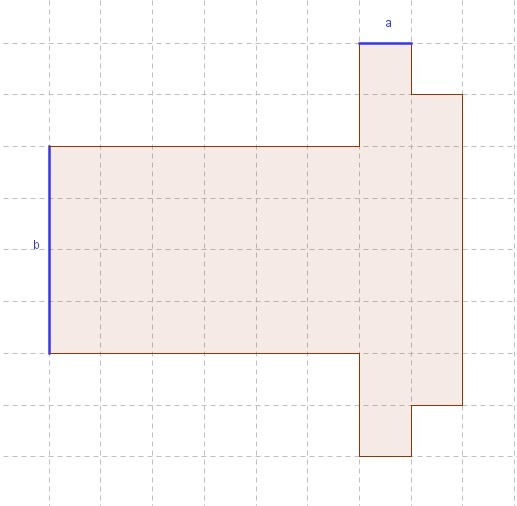
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst. | |||
[[Bild: | |||
[[Bild:einstiegsaufg_termaufstellen2neu.jpg|center|600px]] | |||
< | {{Lösung versteckt|1= | ||
A(a | <math>A(a,b)= 8 \cdot a \cdot b + 6 \cdot a \cdot a = 8ab+6a^2 </math> | ||
[[Bild:Einstiegsaufg_termaufstellen_lösungneu.jpg|center|600px]] | |||
}} | |||
Setze nun für a=1cm und b=4cm ein | Setze nun für a=1cm und b=4cm ein | ||
< | {{Lösung versteckt|1= | ||
A(1 | <math>A(1,4)= 8 \cdot 1cm \cdot 4cm+6 \cdot (1cm)^2 = 32cm^2+6 \cdot 1cm^2 = 32cm^2 + 6cm^2 = 38 cm^2</math> | ||
}} | |||
===Erklärung:=== | |||
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen: | |||
Das Rezept: | |||
#Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit | |||
#Führe eine (oder mehrere) Variable(n) ein | |||
# Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit | #Stelle den Term auf und überlege dir die zugehörige Definitionsmenge | ||
# Führe eine (oder mehrere) Variable(n) ein | |||
# Stelle den Term auf und überlege dir die zugehörige Definitionsmenge | |||
===Beispiel=== | |||
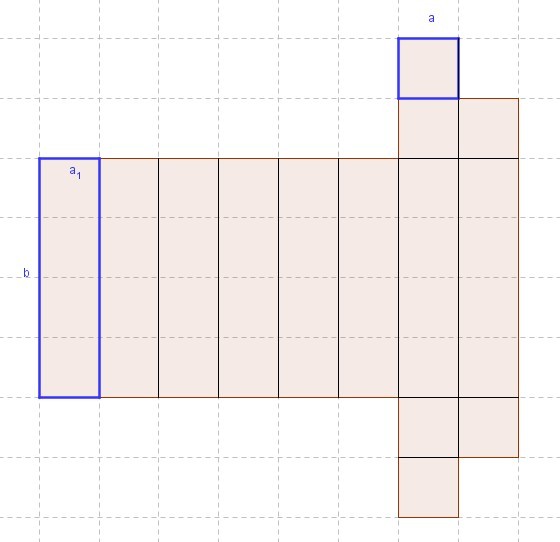
Gehe nach dem "Rezept" vor und stelle einen Term auf, um den Flächeninhalt der Figur zu errechnen. | |||
[[Bild:BspTermaufstellenneu1.jpg]] | |||
[[Bild: | |||
< | {{Lösung versteckt|1= | ||
# Untersuchung des Sachverhalts und Suche nach Gesetzmäßigkeit: Es ist eine Figur gegeben, deren Flächeninhalt unbekannt ist. Die Seitenlängen der Figur sind festgelegt. Betrachtet man die Figur, stellt man fest, dass sie aus mehreren kleinen Rechtecken besteht. Der Flächeninhalt eines einzelnen Rechtecks ist <math> A_R = 2 \cdot 1 </math>. Die Figur besteht aus sechs solchen Rechtecken, also ist der Gesamtflächeninhalt <math> A_F= 6 \cdot 2 \cdot 1 </math> | |||
# Variablen einführen: Wähle für 2=a und für 1=b | |||
# Term aufstellen und Definitionsmenge überlegen: Der Term lautet: <math> 6 \cdot a \cdot b </math> | |||
: Für die Definitionsmenge gilt: Es ist jede Zahl aus <math>\mathbb{Q}</math> einsetzbar ohne Verstoß gegen die Rechenregeln, bei der Berechnung eines Flächeninhalts ist es jedoch sinnvoll, nur positive Zahlen einzusetzen. Also <math>\mathbb{D} = \mathbb{Q}^{+}</math>}} | |||
== | ==Interpretieren von Termen== | ||
===Aufgabenstellung=== | |||
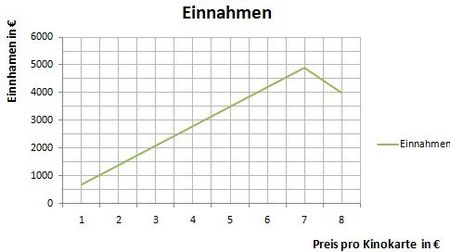
<br />Herr Flimmer ist Besitzer eines Kinos. Er verkauft pro Woche 500 Karten, eine Karte kostet bei ihm 8€. Sein Freund hat für ihn eine Umfrage gemacht, ob eine Senkung des Eintrittspreises seine Einnahmen erhöhen könnte. Sein Ergebnis: Wenn Herr Flimmer seinen Preis um 1 € senken würde, würde er 200 Karten mehr verkaufen. | |||
{| width="99%" | |||
| | | width="40%" style="vertical-align:top" | | ||
| | Aus den Umfragebögen hat er diese Formel zur Berechnung der Einnahmen erstellt: | ||
<math> E(x) = (8 - x) \cdot ( 500 + 200 \cdot x ) </math> | |||
<br /> | <br /> | ||
< | *Überlege, welche Bedeutung das x hat und bei welchem Preis er die meisten Einnahmen hat. | ||
*Wie viele Karten verkauft er dann? | |||
[[Bild:kinodiagramm.jpg|450px|center]] | |||
{{Lösung versteckt|1= | |||
*x steht hier für die Veränderung des Preises [8-x] | |||
:Die Formel bedeutet, dass um jeden Euro, den Herr Flimmer die Kinokarte senkt, ihn 200 Gäste mehr besuchen werden. | |||
:Die größten Einnahmen kann man aus dem Diagramm ablesen: Bei einem Preis von 7 € (Veränderung des Preises um 1 Einheit). Die Einnahmen sind hier 4900€. | |||
*Wenn er die Karten für 7€ verkauft, ändert er seinen ursprünglichen Preis um 1, das heißt er verkauft zu den 500 Karten zusätzlich noch 200, also insgesamt 700 Karten | |||
}} | |||
===Erklärung=== | |||
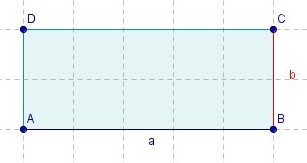
{{Box|1=Erklärung|2=Wenn du einen Term interpretieren oder Aussagen über ihn machen sollst, musst du erst überlegen, welche Bedeutung die Variablen haben. | |||
Zum Beispiel beschreibt <math> a \cdot b </math> den Flächeninhalt eines Rechtecks, wenn a und b die Seitenlängen sind. | |||
[[Bild:rechteck_bspaufg2.2neu.jpg]] | |||
|3=Merksatz}} | |||
===Beispiel=== | |||
Beim Internetprovider "Netzfetz" hat man pro Monat 10 Surfstunden frei. Danach kostet jede angefangene Stunde 2€. Ein anderer Provider, "2&3", bietet 20 freie Surfstunden und verlangt danach für jede angefangene Stunde 4€. | |||
*Stelle für beide Provider einen Term T(x) auf, wobei x die gesurfte Zeit angibt. | |||
{{Lösung versteckt|1= | |||
: Für Netzfetz: <math> T_1 (x) = (x-10) \cdot 2 </math> | |||
: Für 2&3 : <math> T_2 (x) = (x-20) \cdot 4 </math> | |||
}} | |||
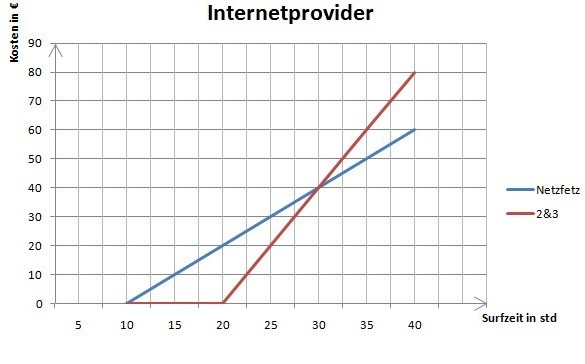
*Erstelle eine Tabelle, die die Kosten der beiden Anbieter gegenüberstellt (für 20std, 25std, 30std, 35std und 40std). Tom und Julia kennen beide Angebote. Tom surft ungefähr 35 Stunden im Monat, Julia nur 25. Welchen Anbieter würdest du Tom empfehlen und welchen sollte Julia wählen? | |||
{{Lösung versteckt|1= | |||
{{{!}} class="wikitable center" | |||
{{!}}- | |||
! Kosten/Surfzeit !! 20 !! 25 !! 30 !! 35 !! 40 | |||
{{!}}- | |||
{{!}} T<sub>1</sub> (x) = (x-10)2 {{!}}{{!}} 20 € {{!}}{{!}} 30 € {{!}}{{!}} 40 € {{!}}{{!}} 50 € {{!}}{{!}} 60 € | |||
{{!}}- | |||
{{!}} T<sub>2</sub> (x) = (x-20)4 {{!}}{{!}} 0 € {{!}}{{!}} 20 € {{!}}{{!}} 40 € {{!}}{{!}} 60 € {{!}}{{!}} 80€ | |||
{{!}}} | |||
Tom surft 35 Stunden: In der Tabelle siehst du die 2 Preise für 35 Stunden Surfzeit. Die Kosten des ersten Terms sind geringer als die des zweiten. Tom sollte, wenn er den günstigeren Anbieter sucht, den Provider Netzfetz wählen. | |||
Julia surft 25 Stunden: Die Kosten des Terms T<sub>2</sub> sind kleiner als die des ersten Terms. Also sollte Julia das Angebot von 2&3 wählen. | |||
}} | |||
*Erstelle mit Hilfe der Tabelle ein Liniendiagramm in deinem Heft.<br /> | |||
{{Lösung versteckt|1= | |||
[[Bild:diagramm_internetprovider2.jpg]] | |||
}} | |||
==Übungsaufgaben== | |||
{{Box|1=Aufgabe 1|2=Übersetze die Rechenvorschrift in einen Term: | |||
a) Addiere 2 zum Quadrat von x | a) Addiere 2 zum Quadrat von x | ||
| Zeile 106: | Zeile 127: | ||
d) Multipliziere x mit seiner Gegenzahl | d) Multipliziere x mit seiner Gegenzahl | ||
{{Lösung versteckt|1= | |||
a) <math>T(x)= x^2+2</math> | |||
b) <math>T(n)= 4n+6</math> | |||
c) <math>T(b)= (b+7)4</math> | |||
d) <math>T(x)= x(-x)</math> | |||
}} | |||
|3=Arbeitsmethode}} | |||
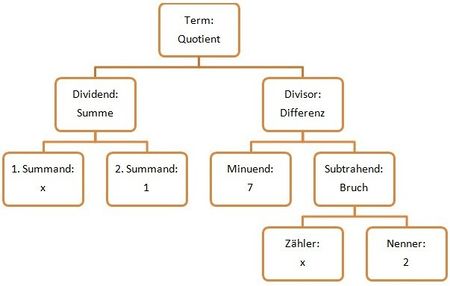
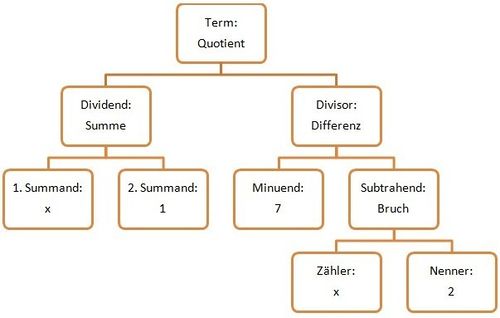
T( | {{Box|1=Aufgabe 2|2=Gib den Term zu folgendem Gliederungsbaum an und berechne seinen Wert für x=4! | ||
[[Bild:termgliederungsbaum2.1.jpg|500px|center]] | |||
{{Lösung versteckt|1= | |||
Der Gliederungsbaum ergibt, wenn man seinen Abzweigungen von oben nach unten richtig folgt, folgenden Term: <math>T(x)= (x+1):(7-\frac{x}{2})</math> | |||
<math>T(4)= (4+1):(7-\frac{4}{2}) = 5:(7-2) = 5:5 = 1 </math> | |||
}} | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Aufgabe 3|2=Laura hat zu schnell von der Tafel abgeschrieben. Dabei hat sie die Werte der Variablen vergessen, nur die Ergebnisse hat sie noch. Hilf ihr die passenden Werte für die Variablen zu finden, wenn der Term T(n)=n<sup>2</sup>+2 lautete. | |||
Warum gibt es | Warum gibt es jeweils zwei Möglichkeiten? | ||
a) T(?)= 18 | a) T(?)= 18 | ||
| Zeile 142: | Zeile 162: | ||
d) T(?)= 6 | d) T(?)= 6 | ||
{{Lösung versteckt|1= | |||
Es gibt zwei Möglichkeiten, da ein Glied des Term n<sup>2</sup> lautet. Eine quadrierte Zahl ist immer positiv. (Bsp.: 3<sup>2</sup>=9=(-3)<sup>2</sup> ) | Es gibt zwei Möglichkeiten, da ein Glied des Term n<sup>2</sup> lautet. Eine quadrierte Zahl ist immer positiv. (Bsp.: 3<sup>2</sup>=9=(-3)<sup>2</sup> ) | ||
a) T(4)= T(-4)= 4 | a) <math>T(4)= T(-4)= 4^2+2= 16+2= 18</math> | ||
b) T(6)= T(-6)= 6 | b) <math>T(6)= T(-6)= 6^2+2= 36+2= 38</math> | ||
c) T(1)= T(-1)= 1 | c) <math>T(1)= T(-1)= 1^2+2= 1+2= 3</math> | ||
d) T(2)= T(-2)= 2 | d) <math>T(2)= T(-2)= 2^2+2= 4+2= 6</math> | ||
}} | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Aufgabe 4|2= | |||
{ | |||
Gib einen Term an, der den Flächeninhalt der abgebildeten Figur berechnet. | |||
{| | |||
Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt. | Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt. | ||
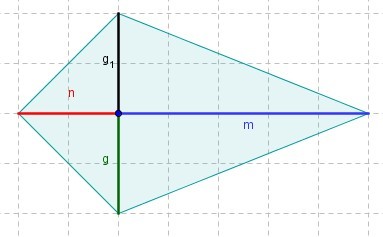
* | * n = 2 cm | ||
* | * m = 5 cm | ||
* | * g = g<sub>1</sub> = 2 cm | ||
<u>Hinweis: Die Figur ist | <u>Hinweis: Die Figur ist achsensymmetrisch.</u> | ||
[[Bild:Drachenviereckneu.jpg|center]] | |||
[[Bild: | {{Lösung versteckt|1= | ||
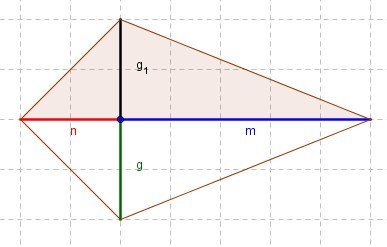
| | [[Bild:Drachenviereck_lösung.jpg|right]] | ||
Das Drachenviereck besteht aus 2 großen (wegen der Achsensymmetrie: gleichgroßen) Dreiecken. Deshalb rechnet man den Flächeninhalt eines Teildreiecks aus und verdoppelt ihn dann. Der Flächeninhalt eines Dreiecks ist allgemein: | |||
Um den Flächeninhalt des Drachenvierecks A<sub>DV</sub> zu erhalten, muss man den Flächeninhalt des Teildreiecks verdoppeln: | <math>A_D = \frac{1}{2} a \cdot h_a </math> | ||
<br />Nun sind die Daten aus der Zeichnung abzulesen. Die Seite a setzt sich in diesem Fall aus m und n zusammen, die Höhe h<sub>a</sub> ist hier g | |||
<br />Der Flächeninhalt für ein Teildreieck ist also: | |||
<math> A_D = \frac{1}{2}(m+n) \cdot g = \frac{1}{2} \cdot (m+n) \cdot g </math> | |||
<br /> | |||
Um den Flächeninhalt des Drachenvierecks A<sub>DV</sub> zu erhalten, muss man den Flächeninhalt des Teildreiecks verdoppeln: | |||
<math> A_{DV}= 2 \cdot A_D = 2 \cdot \frac{1}{2} \cdot (m+n) \cdot g = (m+n) \cdot g </math> | |||
<br /><br /> | |||
<u>Hinweis:</u> Es gibt eine weitere Lösung, wenn man das Drachenviereck in 2 andere Dreiecke aufteilt. | <u>Hinweis:</u> Es gibt eine weitere Lösung, wenn man das Drachenviereck in 2 andere Dreiecke aufteilt. | ||
Der Flächeninhalt kann auch so bestimmt werden: | Der Flächeninhalt kann auch so bestimmt werden: | ||
<math>A_{DV} = \frac{1}{2} (g+g_1)n + \frac{1}{2} (g+g_1) m </math> | |||
Das Ergbenis ist gleich. | Das Ergbenis ist gleich. | ||
<math> A_{DV} = (5cm+2cm) \cdot 2cm = 14cm^2 </math> | |||
}} | |||
|3=Arbeitsmethode}} | |||
{{Fortsetzung|weiter=Umformen von Termen|weiterlink=Terme/Umformen von Termen}} | |||
|} | |||
[[Kategorie:Keine Kategorie]] | |||
Aktuelle Version vom 23. April 2022, 16:02 Uhr
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
Aufgabenstellung
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst.
Setze nun für a=1cm und b=4cm ein
Erklärung:
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Das Rezept:
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Beispiel
Gehe nach dem "Rezept" vor und stelle einen Term auf, um den Flächeninhalt der Figur zu errechnen.
- Untersuchung des Sachverhalts und Suche nach Gesetzmäßigkeit: Es ist eine Figur gegeben, deren Flächeninhalt unbekannt ist. Die Seitenlängen der Figur sind festgelegt. Betrachtet man die Figur, stellt man fest, dass sie aus mehreren kleinen Rechtecken besteht. Der Flächeninhalt eines einzelnen Rechtecks ist . Die Figur besteht aus sechs solchen Rechtecken, also ist der Gesamtflächeninhalt
- Variablen einführen: Wähle für 2=a und für 1=b
- Term aufstellen und Definitionsmenge überlegen: Der Term lautet:
- Für die Definitionsmenge gilt: Es ist jede Zahl aus einsetzbar ohne Verstoß gegen die Rechenregeln, bei der Berechnung eines Flächeninhalts ist es jedoch sinnvoll, nur positive Zahlen einzusetzen. Also
Interpretieren von Termen
Aufgabenstellung
Herr Flimmer ist Besitzer eines Kinos. Er verkauft pro Woche 500 Karten, eine Karte kostet bei ihm 8€. Sein Freund hat für ihn eine Umfrage gemacht, ob eine Senkung des Eintrittspreises seine Einnahmen erhöhen könnte. Sein Ergebnis: Wenn Herr Flimmer seinen Preis um 1 € senken würde, würde er 200 Karten mehr verkaufen.
|
Aus den Umfragebögen hat er diese Formel zur Berechnung der Einnahmen erstellt:
ErklärungErklärung BeispielBeim Internetprovider "Netzfetz" hat man pro Monat 10 Surfstunden frei. Danach kostet jede angefangene Stunde 2€. Ein anderer Provider, "2&3", bietet 20 freie Surfstunden und verlangt danach für jede angefangene Stunde 4€.
Tom surft 35 Stunden: In der Tabelle siehst du die 2 Preise für 35 Stunden Surfzeit. Die Kosten des ersten Terms sind geringer als die des zweiten. Tom sollte, wenn er den günstigeren Anbieter sucht, den Provider Netzfetz wählen. Julia surft 25 Stunden: Die Kosten des Terms T2 sind kleiner als die des ersten Terms. Also sollte Julia das Angebot von 2&3 wählen.
ÜbungsaufgabenAufgabe 1 Übersetze die Rechenvorschrift in einen Term: a) Addiere 2 zum Quadrat von x b) Addiere 6 zum vierfachen der Zahl n c) Multipliziere die Summe aus b und der Zahl 7 mit 4 d) Multipliziere x mit seiner Gegenzahl
a) b) c) d)
Aufgabe 2
Aufgabe 3 Laura hat zu schnell von der Tafel abgeschrieben. Dabei hat sie die Werte der Variablen vergessen, nur die Ergebnisse hat sie noch. Hilf ihr die passenden Werte für die Variablen zu finden, wenn der Term T(n)=n2+2 lautete. Warum gibt es jeweils zwei Möglichkeiten? a) T(?)= 18 b) T(?)= 38 c) T(?)= 3 d) T(?)= 6
Es gibt zwei Möglichkeiten, da ein Glied des Term n2 lautet. Eine quadrierte Zahl ist immer positiv. (Bsp.: 32=9=(-3)2 ) a) b) c) d)
Aufgabe 4 Gib einen Term an, der den Flächeninhalt der abgebildeten Figur berechnet. Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt.
Hinweis: Die Figur ist achsensymmetrisch. Das Drachenviereck besteht aus 2 großen (wegen der Achsensymmetrie: gleichgroßen) Dreiecken. Deshalb rechnet man den Flächeninhalt eines Teildreiecks aus und verdoppelt ihn dann. Der Flächeninhalt eines Dreiecks ist allgemein:
Hinweis: Es gibt eine weitere Lösung, wenn man das Drachenviereck in 2 andere Dreiecke aufteilt. Der Flächeninhalt kann auch so bestimmt werden: Das Ergbenis ist gleich.
|