Sinus- und Kosinusfunktion/3. Allgemeine Sinusfunktion: Unterschied zwischen den Versionen
Main>Florian Ferstl Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (21 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Lernpfad Sinus- und Kosinusfunktion}} | |||
|Lernschritte einblenden|Lernschritte ausblenden}} | |||
==Station 3: Die allgemeine Sinusfunktion== | ==Station 3: Die allgemeine Sinusfunktion== | ||
Sinusfunktionen und Kosinusfunktionen schauen nicht immer gleich aus. | Sinusfunktionen und Kosinusfunktionen schauen nicht immer gleich aus. | ||
z.B. <br><br> | z.B. <br><br> | ||
| Zeile 14: | Zeile 16: | ||
<br><br> | <br><br> | ||
===Was ist was?=== | ===Was ist was?=== | ||
{{Box|1=Üben|2= | |||
Untersuche gezielt und mit Auge für Details, wie sich eine Veränderung der einzelnen Parameter auf den Graphen der Funktion auswirkt. | Untersuche gezielt und mit Auge für Details, wie sich eine Veränderung der einzelnen Parameter auf den Graphen der Funktion auswirkt. | ||
<br> | <br> | ||
<ggb_applet id="X6XAZTDT" width="100%" height="500" border="888888" /> | |||
|3=Üben}} | |||
Halte deine Erkenntniss nun fest: | |||
{{Box|Aufgabe 3 - allgemeine Sinusfunktion|Bearbeite die Aufgabe 3a auf dem [[Media:AB zum Lernpfad Sinus-und Kosinusfunktion.docx|Arbeitsblatt]].|Arbeitsmethode}} | |||
{{Lösung versteckt| | |||
| | |||
a: verändert die Amplitude, also Strecken bzw. Stauchen in y-Richtung<br> | a: verändert die Amplitude, also Strecken bzw. Stauchen in y-Richtung<br> | ||
b: Verschiebung in x-Richtung ''(nach links und rechts)''<br> | b: Verschiebung in x-Richtung ''(nach links und rechts)''<br> | ||
c: verändert die Periodenlänge, also Strecken bzw. Stauchen in x-Richtung<br> | c: verändert die Periodenlänge, also Strecken bzw. Stauchen in x-Richtung<br> | ||
d: Verschieben entlang der y-Achse ''(nach oben und unten)''<br> | d: Verschieben entlang der y-Achse ''(nach oben und unten)''<br> | ||
|Lösung anzeigen|Lösung verbergen}} | |||
<br> | |||
''' | |||
Schreibe folgenden Hefteintrag in dein Schulheft! | |||
''' | |||
{{Box|1=Merke|2= | |||
Die allgemeine Sinuskurve <math> y = a\cdot sin(b\cdot(x-c)+d </math> geht so aus der normalen Sinuskurve <math> y=sin(x)</math> hervor: <br> | |||
* Die Amplitude ist der Betrag von a . Die y-Werte liegen also zwischen -a und a. Bei negativem a wird noch an der x-Achse gespiegelt. | |||
* Die Periode ist <math> \frac{2\pi}{b} </math> | |||
* Verschiebung um c in x-Richtung | |||
* Verschiebung um d in y-Richtung | |||
<br> | |||
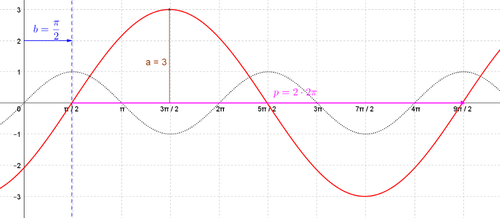
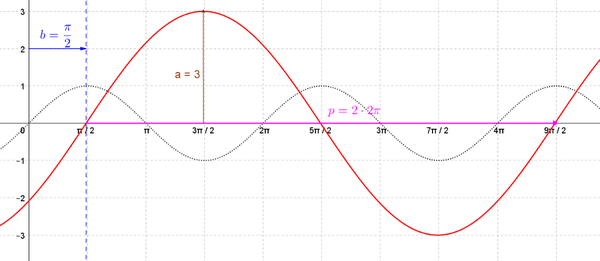
'''<u>Beispiel:</u>''' <br><br> | |||
<math> y = 3\cdot sin(0.5\cdot(x-\pi)) </math> bedeutet | |||
* Amplitude ist 3 | |||
* Periode ist <math> \frac{2 \pi}{0.5}= 4\cdot \pi</math> | |||
* Verschiebung um <math> \pi</math> in positive x-Richtung ("nach rechts") | |||
* keine Verschiebung in y-Richtung | |||
<br> | |||
[[Datei:Beispiel Sinus.png|left|600px|Beispiel Sinus]] | |||
|3=Merksatz}} | |||
<br> | <br> | ||
<br> | |||
''' | {{Box|Aufgabe - 3 allgemeine Sinusfunktion|Bearbeite die '''Aufgabe 3b''' auf dem [[Media:AB zum Lernpfad Sinus-und Kosinusfunktion.docx|Arbeitsblatt]].|Arbeitsmethode}} | ||
<br> | |||
<br> | <br> | ||
{| | {| | ||
'''Ok, jetzt schauen wir uns die drei Parameter noch etwas genauer an. Have fun...! | |||
{{Fortsetzung|weiter=Weiter|weiterlink=/3.1 Parameter}} | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:GeoGebra]] | |||
Aktuelle Version vom 6. Dezember 2024, 22:21 Uhr
Station 3: Die allgemeine Sinusfunktion
Sinusfunktionen und Kosinusfunktionen schauen nicht immer gleich aus.
z.B.
Allgemein:
In dieser Station findest du heraus, wie sich die vier Parameter a, b, c und d auf den Verlauf des Graphen auswirken. Viel Spass!
Was ist was?
Untersuche gezielt und mit Auge für Details, wie sich eine Veränderung der einzelnen Parameter auf den Graphen der Funktion auswirkt.

Halte deine Erkenntniss nun fest:
a: verändert die Amplitude, also Strecken bzw. Stauchen in y-Richtung
b: Verschiebung in x-Richtung (nach links und rechts)
c: verändert die Periodenlänge, also Strecken bzw. Stauchen in x-Richtung
d: Verschieben entlang der y-Achse (nach oben und unten)
Schreibe folgenden Hefteintrag in dein Schulheft!
Die allgemeine Sinuskurve geht so aus der normalen Sinuskurve hervor:
- Die Amplitude ist der Betrag von a . Die y-Werte liegen also zwischen -a und a. Bei negativem a wird noch an der x-Achse gespiegelt.
- Die Periode ist
- Verschiebung um c in x-Richtung
- Verschiebung um d in y-Richtung
Beispiel:
bedeutet
- Amplitude ist 3
- Periode ist
- Verschiebung um in positive x-Richtung ("nach rechts")
- keine Verschiebung in y-Richtung