Sinus- und Kosinusfunktion/2.1 Sinusfunktion: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Florian Ferstl
Keine Bearbeitungszusammenfassung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(19 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Lernpfad Sinus und Kosinusfunktion}}
{{Navigation verstecken|{{Lernpfad Sinus- und Kosinusfunktion}}
 
|Lernschritte einblenden|Lernschritte ausblenden}}
 
<div style="  width:100%; border: 2px solid #c6d745; background-color:#c6d745; padding:7px;font-size:1px; height:1px; border-bottom:1px solid #c6d745;"></div>
<div style="  width: 100%; border: 2px solid #c6d745; background-color:#ffffff; align:center; padding:7px;">


==Station 2: Sinusfunktion und Kosinusfunktion==
==Station 2: Sinusfunktion und Kosinusfunktion==


{|
===2.1 Sinusfunktion===


==2.1 Sinusfunktion==
{{Box|1=Üben|2=
{{Auftrag|
Versuche dir nochmal klarzumachen, wie die Sinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). <br>
Versuche dir nochmal klarzumachen, wie die Sinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). <br>
Nun tragen wir die Sinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein.  
Nun tragen wir die Sinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein.  
<br>Durch Klick auf die Checkbox „Sinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.<br>
<br>Durch Klick auf die Checkbox „Sinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.
<iframe scrolling="no" title="Sinusfunktion am Einheitskreis" src="https://www.geogebra.org/material/iframe/id/TTDQ956P/width/1727/height/664/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="980" height="364px" style="border:0px;"> </iframe> }}<br>
<br><br>
<ggb_applet id="TTDQ956P" width="100%" height="500" />
 
|3=Üben}}




<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br>
Halte deine Erkenntnisse nun schriftlich fest:
Halte deine Erkenntnisse nun schriftlich fest:


{{Aufgaben-M|2.1 Sinusfunktion|Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.}}
{{Box|Aufgabe - 2.1 Sinusfunktion|Bearbeite den zugehörigen Auftrag auf dem [[Media:AB zum Lernpfad Sinus-und Kosinusfunktion.docx|Arbeitsblatt]].|Arbeitsmethode}}
<br>
<br>
Teste, ob du alles verstanden hast!
Teste, ob du alles verstanden hast!
{{Übung|'''Sinusfunktion verstanden?'''  
 
{{Box|Üben|'''Sinusfunktion verstanden?'''  
<br>
<br>
{{LearningApp|app=p97643u9t17|width=100%|height=400px}}


<iframe src="https://learningapps.org/watch?v=p97643u9t17" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}
|Üben}}
 
 
 
 
 
----
'''Und weiter geht's zur Kosinusfunktion. Ist ja ganz ähnlich...
{|border="0" cellspacing="0" cellpadding="4"
|align = "left" width="60"|[[Datei:Pfeil weiter.png|50px]]
|align = "left"|[[/2.2 Kosinusfunktion|'''Hier geht es weiter''']]'''...'''
|}




{{Fortsetzung|weiter=Kosinusfunktion|weiterlink=../2.2 Kosinusfunktion}}






{{Lernpfad Sinus und Kosinusfunktion}}
[[Kategorie:Interaktive Übung]]
[[Kategorie:GeoGebra]]
[[Kategorie:LearningApps]]

Aktuelle Version vom 6. Dezember 2024, 22:13 Uhr

Sinus- und Kosinusfunktion
  1. Bogenmaß
    Beispiel Sinus.png
  2. Sinusfunktion
  3. Kosinusfunktion
  4. Allgemeine Sinusfunktion
  5. Allgemeine Sinusfunktion - Parameter
  6. Übung 1
  7. Übung 2
  8. Abschluss
  9. Tangensfunktion
Mathematik-digital.de

Station 2: Sinusfunktion und Kosinusfunktion

2.1 Sinusfunktion

Üben

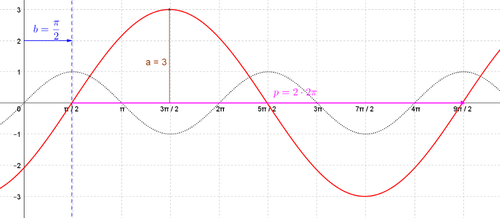
Versuche dir nochmal klarzumachen, wie die Sinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie).
Nun tragen wir die Sinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein.
Durch Klick auf die Checkbox „Sinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.

GeoGebra


Halte deine Erkenntnisse nun schriftlich fest:

Aufgabe - 2.1 Sinusfunktion
Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.


Teste, ob du alles verstanden hast!

Üben

Sinusfunktion verstanden?



Kosinusfunktion
Abgerufen von „https://unterrichten.zum.de/index.php?title=Sinus-_und_Kosinusfunktion/2.1_Sinusfunktion&oldid=139054“