Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Flächeninhalt eines Rechtecks - Aufgaben: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Maria Eirich Keine Bearbeitungszusammenfassung |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (77 dazwischenliegende Versionen von 10 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{TOCright}} | |||
{{Box|Aufgabensammlung| | |||
*Aufgaben rund um den Flächeninhalt | |||
*[[Media:Wimmelbild Rechteck.docx|Arbeitsblatt Wimmelbild]] | |||
[[Datei:Logo Mathematik-digital 2011.png|200px|right|verweis=Mathematik-digital|Mathematik-digital]] | |||
|Lernpfad}} | |||
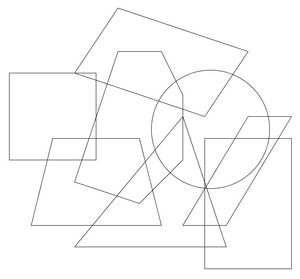
{{Box|Färbe alle Rechtecke gelb| | |||
*Drucke das Arbeitsblatt aus und male alle Rechtecke gelb aus. | |||
*Wie viele Rechtecke hast du gefunden? | |||
[[Datei:Wimmelbild.jpg|300px|center]] | |||
|Arbeitsmethode}} | |||
{{Lösung versteckt| | |||
:Es gibt zwei Rechtecke | |||
[[Datei:Wimmelbild Lösung.jpg|300px|center]] | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
==Wir merken uns== | |||
== | {{Box|1=Merke|2= | ||
[[File:Prostokat-rectangle.svg|100px|right]] | |||
*<big>Flächeninhalt</big> <math>A =a\cdot b</math> | |||
*<big>Umfang</big> <math>U = 2\cdot a + 2 \cdot b = 2\cdot(a + b)</math> | |||
|3=Merksatz}} | |||
Bei dieser Aufgabe sind abwechselnd die Länge, die Breite, der Umfang oder der Flächeninhalt eines Rechtecks gegeben. Du sollst jeweils die fehlenden Werte ermitteln. [http://www.realmath.de/Neues/Klasse6/grundwissen/rechteck.html Hier gehts zu den Übungen mit Highscore-Liste]. | |||
==Was stimmt hier nicht?== | |||
Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen. | |||
Paul misst die beiden Kinderzimmer aus: Das erste ist 5 m lang und 4 m breit, das zweite 6 m lang und 3 m breit. | |||
Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9." | |||
Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an. | |||
{{Lösung versteckt|1= | |||
Noras Lösung ist falsch. Sie addiert die Länge und Breite anstatt den Flächeninhalt zu berechnen. | |||
1. Zimmer: 5cm * 4cm = 20cm<sup>2</sup> | |||
2. Zimmer: 6cm * 3cm = 18cm<sup>2</sup> | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
==Wie groß ist die gelbe Fläche?== | ==Wie groß ist die gelbe Fläche?== | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 49: | Zeile 63: | ||
</quiz> | </quiz> | ||
==Fußballfeld der Allianz Arena== | |||
== Fußballfeld der Allianz Arena == | |||
[[Bild:Allianzarenapano.jpg|750px|center]] | [[Bild:Allianzarenapano.jpg|750px|center]] | ||
| Zeile 64: | Zeile 71: | ||
#Schätze die Größe des Feldes. | #Schätze die Größe des Feldes. | ||
#Suche dir nun die entsprechenden Maße im Internet und berechne die Fläche des Fußballfeldes genau. | #Suche dir nun die entsprechenden Maße im Internet und berechne die Fläche des Fußballfeldes genau. | ||
#Die Größe eines Rasenstücke vom Typ "Powerrasen" beträgt: 2 m x 10 m. Wie viele Rasenstücke wurden etwa verlegt? | #Die Größe eines Rasenstücke vom Typ "Powerrasen" beträgt: 2 m x 10 m. Wie viele Rasenstücke wurden etwa verlegt? | ||
{{Lösung versteckt|1= | |||
#ungefähr 8000 m<sup>2</sup> | |||
#'''netto''' (Fußballfeld): 68 m x 105 m = 7140 m<sup>2</sup>; '''brutto''' (gesamte Rasenfläche): 72 m x 111 m = 7992 m<sup>2</sup> | |||
#8000m<sup>2</sup> : 20 m<sup>2</sup> = 400 | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
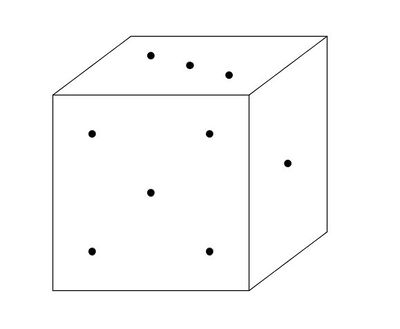
==Oberfläche des Würfels== | |||
[[Bild:Viereck7.jpg|400px|right]] | |||
#Wie groß ist die Oberfläche eines Würfels mit der Kantenlänge 1 cm? | |||
#Wie groß ist die Oberfläche wenn man die Kantenlänge verdoppelt? | |||
#Weißt du auch, wie lange alle Kanten zusammen sind? | |||
{{Lösung versteckt|1= | |||
#6cm<sup>2</sup> | |||
#24cm<sup>2</sup> | |||
#12 cm | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
==Das Rechteck Quiz== | |||
<quiz display="simple"> | |||
{Welche Aussagen treffen zu? Kreuze an:} | |||
+ In einem Rechteck sind alle Diagonalen gleich lang. | |||
- In einem Rechteck stehen die Diagonlane immer senkrecht aufeinander. | |||
- Jedes Rechteck ist ein Quadrat. | |||
+ In einem Rechteck sind gegenüberliegende Seiten gleich lang. | |||
+ In einem Rechteck sind gegenüberliegende Seiten parallel. | |||
- Wenn sich in einem Rechteck der Umfang verdoppelt, verdoppelt sich auch der Flächeninhalt. | |||
- Jedes Rechteck hat 4 Symmetrieachsen. | |||
+ In einem Rechteck sind benachbarte Seiten zueinander senkrecht. | |||
+ In einem Rechteck sind alle Winkel gleich groß. | |||
</quiz> | |||
==Rechteck und Quadrat== | |||
{{LearningApp|app=28517396|width=100%|height=650px}} | |||
* [https://learningapps.org/28517396 auf LearningApps] | |||
==Flächeninhalt und Umfang== | |||
{{LearningApp|app=102321|width=100%|height=500px}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Sekundarstufe_1]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Interaktive Übung]] | |||
Aktuelle Version vom 17. Januar 2023, 09:26 Uhr
Aufgabensammlung
- Aufgaben rund um den Flächeninhalt
- Arbeitsblatt Wimmelbild
Färbe alle Rechtecke gelb
Wir merken uns
Bei dieser Aufgabe sind abwechselnd die Länge, die Breite, der Umfang oder der Flächeninhalt eines Rechtecks gegeben. Du sollst jeweils die fehlenden Werte ermitteln. Hier gehts zu den Übungen mit Highscore-Liste.
Was stimmt hier nicht?
Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen.
Paul misst die beiden Kinderzimmer aus: Das erste ist 5 m lang und 4 m breit, das zweite 6 m lang und 3 m breit.
Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9."
Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an.
Noras Lösung ist falsch. Sie addiert die Länge und Breite anstatt den Flächeninhalt zu berechnen.
1. Zimmer: 5cm * 4cm = 20cm2
2. Zimmer: 6cm * 3cm = 18cm2
Wie groß ist die gelbe Fläche?
Fußballfeld der Allianz Arena
- Schätze die Größe des Feldes.
- Suche dir nun die entsprechenden Maße im Internet und berechne die Fläche des Fußballfeldes genau.
- Die Größe eines Rasenstücke vom Typ "Powerrasen" beträgt: 2 m x 10 m. Wie viele Rasenstücke wurden etwa verlegt?
- ungefähr 8000 m2
- netto (Fußballfeld): 68 m x 105 m = 7140 m2; brutto (gesamte Rasenfläche): 72 m x 111 m = 7992 m2
- 8000m2 : 20 m2 = 400
Oberfläche des Würfels
- Wie groß ist die Oberfläche eines Würfels mit der Kantenlänge 1 cm?
- Wie groß ist die Oberfläche wenn man die Kantenlänge verdoppelt?
- Weißt du auch, wie lange alle Kanten zusammen sind?
- 6cm2
- 24cm2
- 12 cm
Das Rechteck Quiz
Rechteck und Quadrat
Flächeninhalt und Umfang