Gruppenpuzzle: Unterschied zwischen den Versionen
K (→[[Mathematik]]: +Erläuterung) |
K (kat) |
||
| (42 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{ | [[Datei:Gruppenpuzzle.png|miniatur|300px|Gruppenpuzzle]] | ||
{{Box|Als Gruppenpuzzle| | |||
:bezeichnet man eine Methode des '''kooperativen Lernens'''. Dabei werden die Teilnehmer von gleich großen Arbeitsgruppen abwechselnd zu Stamm- und zu Expertengruppen zusammengesetzt. Die Analogie zum Puzzle besteht darin, dass eine Stammgruppe in "Puzzleteile" "zerschnitten" und dann die Puzzleteile zu einem neuen "Bild", der Expertenrunde, und schließlich wieder zur Stammgruppe zusammengesetzt werden. - Statt "zerlegen" kann man auch (bildlich gesprochen) "zersägen" sagen. | |||
:Daher kommt der englische Ausdruck '''jigsaw''' für ''Gruppenpuzzle'' (von engl. "saw": Säge). | |||
|Hervorhebung1}} | |||
==Das Problem und die Lösung== | |||
Gruppenarbeit soll die Eigenständigkeit und Eigenverantwortung des Lerners fördern, läuft aber oft so ab, dass Einzelne in der Gruppe die Arbeit erledigen und die Anderen sich führen lassen. Das geht bis hin zum Präsentieren der Gruppenergebnisse. Das erarbeitete und/oder präsentierte Ergebnis spiegelt folglich nicht den Wissensstand der einzelnen Gruppenmitglieder wieder - ''davon gehen aber Lehrerin oder Lehrer gerne aus''. Die Gruppenarbeit nützt wieder einmal denjenigen am meisten, die auch sonst initiativ, neugierig und zielorientiert sind. | |||
'''Die Lösung''' | |||
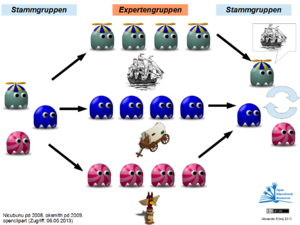
Im Gruppenpuzzle unterweisen Schüler ihre Mitschüler. Jeder ist Experte und Wissensvermittler zugleich. Experte wird er dadurch, dass er einen Spezialauftrag erhält, als Vermittler seines Expertenwissens betätigt er sich dann, wenn er sein Wissen in eine Gruppe einbringt. Unterschieden wird also zwischen Expertengruppen und Stammgruppen. Aus den Beiträgen der Experten wird dann in den Stammgruppen ein Gesamtbild zusammengesetzt: Das fertige Puzzle! [[Bild:Gruppenpuzzle.jpg|thumb|300px|Gruppenpuzzle-Schema]] | |||
[[Datei:Gruppenpuzzle Methode Erklaerung.webm|mini|Erklärvideo: Vorgehen zur Methode Gruppenpuzzle]] | |||
Zur Organisation: | Zur Organisation: | ||
:Man stelle sich z.B. drei Großfamilien vor, die Maiers, die Müllers und die Schneiders. In jeder Familie gibt es eine Mutter, einen Vater, einen Sohn, eine Tochter und vielleicht noch einen Großvater, die Zahl der Familienmitglieder ist beliebig erweiterbar. Alle drei Familien haben beschlossen, zusammen in Urlaub zu fahren, wissen aber noch nicht wohin und wollen sich informieren. Sie machen dies arbeitsteilig: | :Man stelle sich z.B. drei Großfamilien vor, die Maiers, die Müllers und die Schneiders. In jeder Familie gibt es eine Mutter, einen Vater, einen Sohn, eine Tochter und vielleicht noch einen Großvater, die Zahl der Familienmitglieder ist beliebig erweiterbar. Alle drei Familien haben beschlossen, zusammen in Urlaub zu fahren, wissen aber noch nicht wohin und wollen sich informieren. Sie machen dies arbeitsteilig: | ||
:Am ersten Tag setzen sich jeweils alle Mütter, alle Väter, alle Söhne und alle Töchter zusammen und studieren Reiseführer: Die Väter einen Reiseführer über die Toscana, die Mütter über Tenerifa, die Töchter über Mallorca und die Söhne über die Bretagne. Somit sind Väter, Mütter, Söhne und Töchter jeweils Experten für dieses "Gebiet". | :Am ersten Tag setzen sich jeweils alle Mütter, alle Väter, alle Söhne und alle Töchter zusammen und studieren Reiseführer: Die Väter einen Reiseführer über die Toscana, die Mütter über Tenerifa, die Töchter über Mallorca und die Söhne über die Bretagne. Somit sind Väter, Mütter, Söhne und Töchter jeweils Experten für dieses "Gebiet". | ||
:Am zweiten Tag halten die Maiers, die Müllers und die Schneiders getrennt ihren Familienrat ab. Vater wird jetzt über die Toscana, Mutter über Teneriffa, die Tochter über Mallorca und der Sohn über die Bretagne informieren; sie werden vergleichen, nachfragen und sich vorläufige Gedanken machen. | :Am zweiten Tag halten die Maiers, die Müllers und die Schneiders getrennt ihren Familienrat ab. Vater wird jetzt über die Toscana, Mutter über Teneriffa, die Tochter über Mallorca und der Sohn über die Bretagne informieren; sie werden vergleichen, nachfragen und sich vorläufige Gedanken machen. | ||
:Am dritten Tag machen die drei Familien eine Großversammlung (bei Wein, Bier, Sprudel und Cola). Jeder dürfte jetzt über jedes Reiseland gut Bescheid wissen und zusätzlich Teneriffa- oder Mallorca-Experte sein. Jetzt können sie kompetent diskutieren und sich hoffentlich auf ein Reiseziel einigen. Damit sind, kurz gesagt, drei mal vier Leute (=12) gleichzeitig Lernende und Lehrer gewesen. | :Am dritten Tag machen die drei Familien eine Großversammlung (bei Wein, Bier, Sprudel und Cola). Jeder dürfte jetzt über jedes Reiseland gut Bescheid wissen und zusätzlich Teneriffa- oder Mallorca-Experte sein. Jetzt können sie kompetent diskutieren und sich hoffentlich auf ein Reiseziel einigen. Damit sind, kurz gesagt, drei mal vier Leute (=12) gleichzeitig Lernende und Lehrer gewesen. | ||
==Organisationsformen== | ==Organisationsformen== | ||
{{Box|| | |||
Um Stamm- und Expertengruppen zu bilden, eignen sich verschiedene Hilfsmittel und Modelle, die letztlich alle auf eine Gruppenbildung nach dem Zufallsprinzip hinauslaufen: | |||
;Spielkartensatz, bestehend aus 32 Karten: | |||
:Vier Farben (Herz/Caro/Kreuz/Blatt) | :Vier Farben (Herz/Caro/Kreuz/Blatt) → Stammgruppen, | ||
:Bilder (Bube/Dame/König/Ass/...) | :Bilder (Bube/Dame/König/Ass/...) → Expertengruppen | ||
:Bei kleineren Klassen können einzelne Bilder (alle Siebener, Achter oder Neuner) herausgenommen werden, dann gibt es dementsprechend weniger Expertengruppen. | :Bei kleineren Klassen können einzelne Bilder (alle Siebener, Achter oder Neuner) herausgenommen werden, dann gibt es dementsprechend weniger Expertengruppen. | ||
;Fußballmannschaften: | |||
: Hertha BSC Berlin, VfB Stuttgart, FC Bayern, HSV Hamburg ... | : Hertha BSC Berlin, VfB Stuttgart, FC Bayern, HSV Hamburg ... → Stammgruppen | ||
: Torwart, rechter/linker Verteidiger, Mittelstürmer, Libero ... | : Torwart, rechter/linker Verteidiger, Mittelstürmer, Libero ... → Expertengruppen | ||
: Auch hier können beliebig viele Expertengruppen gebildet werden, je nach Klassengröße. | : Auch hier können beliebig viele Expertengruppen gebildet werden, je nach Kurs/Klassengröße. | ||
;Familien: | |||
: Familie Mayer, Familie Müller, Familie Zimmermann, die Albertis | : Familie Mayer, Familie Müller, Familie Zimmermann, die Albertis ... → Stammgruppen | ||
: Vater, Mutter, Tochter, Sohn, Tante, Großvater ... | : Vater, Mutter, Tochter, Sohn, Tante, Großvater ... → Expertengruppen | ||
: Die Stammgruppen sollen sich die Namen selbst geben! Achtung, ältere Schüler finden diese Familiengeschichte eher albern und wollen nicht Opa oder Tante sein. | : Die Stammgruppen sollen sich die Namen selbst geben! Achtung, ältere Schüler finden diese Familiengeschichte eher albern und wollen nicht Opa oder Tante sein. | ||
|Hervorhebung2}} | |||
==Das Gruppenpuzzle im Fachunterricht== | ==Das Gruppenpuzzle im Fachunterricht== | ||
===Deutsch=== | |||
{{Box|Inhaltssicherung zu B. Brechts "Leben des Galilei" im Gruppenpuzzle| | |||
1. Schritt: | 1. Schritt: | ||
Die Inhaltserfassung der Bilder 1 bis 3 findet gemeinsam im Klassenverband statt, und zwar, indem exemplarisch folgendes Schema ausgefüllt wird (Arbeitsblatt): | Die Inhaltserfassung der Bilder 1 bis 3 findet gemeinsam im Klassenverband statt, und zwar, indem exemplarisch folgendes Schema ausgefüllt wird (Arbeitsblatt): | ||
<pre> | |||
Bild | Ort | Zeit | Personen | Handlung | Motive | Thema | Bemerk. | Bild | Ort | Zeit | Personen | Handlung | Motive | Thema | Bemerk. | ||
-----|-------|--------|----------|-------------------|--------|-------|-------- | -----|-------|--------|----------|-------------------|--------|-------|-------- | ||
| Zeile 78: | Zeile 57: | ||
-----|-------|--------|----------|-------------------|--------|-------|-------- | -----|-------|--------|----------|-------------------|--------|-------|-------- | ||
3 | | | | | | | | 3 | | | | | | | | ||
</pre> | |||
2. Schritt: Jetzt wird das Gruppenpuzzle organisiert. | 2. Schritt: Jetzt wird das Gruppenpuzzle organisiert. | ||
| Zeile 84: | Zeile 63: | ||
Bilden Sie Stammgruppen zu je vier Teilnehmern. Diese sollen sich kurz zusammensetzen und sich einen Namen geben. Wie wäre es mit Namen von berühmten Naturwissenschaftlern: Kopernikus, Kepler, Brahe, Bruno, Newton, Gauß. In jeder Gruppe werden nun dieselben vier Rollen verteilt: z.B. Meister, Meisterin, Sohn und Tochter, oder auch nur die Nummern 1, 2, 3 und 4, das ist schön wissenschaftlich-abstrakt. Dieser ganze Vorgang sollte nicht länger als 10 Minuten dauern, führt aber zu klaren Zuordnungen und zu Identifikationen mit berühmten Namen: Ich Kepler 1, du Newton 3, sie Kopernikus 2. | Bilden Sie Stammgruppen zu je vier Teilnehmern. Diese sollen sich kurz zusammensetzen und sich einen Namen geben. Wie wäre es mit Namen von berühmten Naturwissenschaftlern: Kopernikus, Kepler, Brahe, Bruno, Newton, Gauß. In jeder Gruppe werden nun dieselben vier Rollen verteilt: z.B. Meister, Meisterin, Sohn und Tochter, oder auch nur die Nummern 1, 2, 3 und 4, das ist schön wissenschaftlich-abstrakt. Dieser ganze Vorgang sollte nicht länger als 10 Minuten dauern, führt aber zu klaren Zuordnungen und zu Identifikationen mit berühmten Namen: Ich Kepler 1, du Newton 3, sie Kopernikus 2. | ||
Daraufhin bilden sich die Expertengruppen: Alle Meister (oder Einser), Meisterinnen (Zweier) usw. treffen sich, erhalten ein leeres Formblatt (wie oben) und dazu folgenden | Daraufhin bilden sich die Expertengruppen: Alle Meister (oder Einser), Meisterinnen (Zweier) usw. treffen sich, erhalten ein leeres Formblatt (wie oben) und dazu folgenden Arbeitsauftrag: | ||
Gruppe 1: Tragen Sie für die Bilder 4 bis 6 alle wichtigen Informationen ein. | :Gruppe 1: Tragen Sie für die Bilder 4 bis 6 alle wichtigen Informationen ein. | ||
Gruppe 2: Tragen Sie für die Bilder 7 bis 9 alle wichtigen Informationen ein. | :Gruppe 2: Tragen Sie für die Bilder 7 bis 9 alle wichtigen Informationen ein. | ||
Gruppe 3: Tragen Sie für die Bilder 10 bis 12 alle wichtigen Informationen ein. | :Gruppe 3: Tragen Sie für die Bilder 10 bis 12 alle wichtigen Informationen ein. | ||
Gruppe 4: Tragen Sie für die Bilder 13 bis 15 alle wichtigen Informationen ein. | :Gruppe 4: Tragen Sie für die Bilder 13 bis 15 alle wichtigen Informationen ein. | ||
3. Schritt: | 3. Schritt: | ||
| Zeile 99: | Zeile 78: | ||
Formen der Auswertung und Weiterarbeit? | Formen der Auswertung und Weiterarbeit? | ||
:a) Die Stammgruppen fügen ihre vier Formblätter - eventuell überarbeitet und verschönert - zu einem Poster zusammen und hängen dies auf. | |||
:b) Jeder einzelne Schüler füllt jetzt für sich das obige Struktur-Diagramm aus (als Hausaufgabe). In der Stunde wird dann verglichen und ergänzt, entweder im Plenum oder wieder in den Stammgruppen. | |||
:c) Eine Leistungsmessung findet nicht statt | |||
(Klaus Dautel) | |||
|Üben}} | |||
[[Kategorie:Kooperatives Lernen]] | |||
[[Kategorie:Deutsch]] | |||
[[Kategorie: | |||
[[Kategorie:Methode]] | [[Kategorie:Methode]] | ||
Aktuelle Version vom 15. Dezember 2021, 09:42 Uhr
- bezeichnet man eine Methode des kooperativen Lernens. Dabei werden die Teilnehmer von gleich großen Arbeitsgruppen abwechselnd zu Stamm- und zu Expertengruppen zusammengesetzt. Die Analogie zum Puzzle besteht darin, dass eine Stammgruppe in "Puzzleteile" "zerschnitten" und dann die Puzzleteile zu einem neuen "Bild", der Expertenrunde, und schließlich wieder zur Stammgruppe zusammengesetzt werden. - Statt "zerlegen" kann man auch (bildlich gesprochen) "zersägen" sagen.
- Daher kommt der englische Ausdruck jigsaw für Gruppenpuzzle (von engl. "saw": Säge).
Das Problem und die Lösung
Gruppenarbeit soll die Eigenständigkeit und Eigenverantwortung des Lerners fördern, läuft aber oft so ab, dass Einzelne in der Gruppe die Arbeit erledigen und die Anderen sich führen lassen. Das geht bis hin zum Präsentieren der Gruppenergebnisse. Das erarbeitete und/oder präsentierte Ergebnis spiegelt folglich nicht den Wissensstand der einzelnen Gruppenmitglieder wieder - davon gehen aber Lehrerin oder Lehrer gerne aus. Die Gruppenarbeit nützt wieder einmal denjenigen am meisten, die auch sonst initiativ, neugierig und zielorientiert sind.
Die Lösung
Im Gruppenpuzzle unterweisen Schüler ihre Mitschüler. Jeder ist Experte und Wissensvermittler zugleich. Experte wird er dadurch, dass er einen Spezialauftrag erhält, als Vermittler seines Expertenwissens betätigt er sich dann, wenn er sein Wissen in eine Gruppe einbringt. Unterschieden wird also zwischen Expertengruppen und Stammgruppen. Aus den Beiträgen der Experten wird dann in den Stammgruppen ein Gesamtbild zusammengesetzt: Das fertige Puzzle!
Zur Organisation:
- Man stelle sich z.B. drei Großfamilien vor, die Maiers, die Müllers und die Schneiders. In jeder Familie gibt es eine Mutter, einen Vater, einen Sohn, eine Tochter und vielleicht noch einen Großvater, die Zahl der Familienmitglieder ist beliebig erweiterbar. Alle drei Familien haben beschlossen, zusammen in Urlaub zu fahren, wissen aber noch nicht wohin und wollen sich informieren. Sie machen dies arbeitsteilig:
- Am ersten Tag setzen sich jeweils alle Mütter, alle Väter, alle Söhne und alle Töchter zusammen und studieren Reiseführer: Die Väter einen Reiseführer über die Toscana, die Mütter über Tenerifa, die Töchter über Mallorca und die Söhne über die Bretagne. Somit sind Väter, Mütter, Söhne und Töchter jeweils Experten für dieses "Gebiet".
- Am zweiten Tag halten die Maiers, die Müllers und die Schneiders getrennt ihren Familienrat ab. Vater wird jetzt über die Toscana, Mutter über Teneriffa, die Tochter über Mallorca und der Sohn über die Bretagne informieren; sie werden vergleichen, nachfragen und sich vorläufige Gedanken machen.
- Am dritten Tag machen die drei Familien eine Großversammlung (bei Wein, Bier, Sprudel und Cola). Jeder dürfte jetzt über jedes Reiseland gut Bescheid wissen und zusätzlich Teneriffa- oder Mallorca-Experte sein. Jetzt können sie kompetent diskutieren und sich hoffentlich auf ein Reiseziel einigen. Damit sind, kurz gesagt, drei mal vier Leute (=12) gleichzeitig Lernende und Lehrer gewesen.
Organisationsformen
Um Stamm- und Expertengruppen zu bilden, eignen sich verschiedene Hilfsmittel und Modelle, die letztlich alle auf eine Gruppenbildung nach dem Zufallsprinzip hinauslaufen:
- Spielkartensatz, bestehend aus 32 Karten
- Vier Farben (Herz/Caro/Kreuz/Blatt) → Stammgruppen,
- Bilder (Bube/Dame/König/Ass/...) → Expertengruppen
- Bei kleineren Klassen können einzelne Bilder (alle Siebener, Achter oder Neuner) herausgenommen werden, dann gibt es dementsprechend weniger Expertengruppen.
- Fußballmannschaften
- Hertha BSC Berlin, VfB Stuttgart, FC Bayern, HSV Hamburg ... → Stammgruppen
- Torwart, rechter/linker Verteidiger, Mittelstürmer, Libero ... → Expertengruppen
- Auch hier können beliebig viele Expertengruppen gebildet werden, je nach Kurs/Klassengröße.
- Familien
- Familie Mayer, Familie Müller, Familie Zimmermann, die Albertis ... → Stammgruppen
- Vater, Mutter, Tochter, Sohn, Tante, Großvater ... → Expertengruppen
- Die Stammgruppen sollen sich die Namen selbst geben! Achtung, ältere Schüler finden diese Familiengeschichte eher albern und wollen nicht Opa oder Tante sein.
Das Gruppenpuzzle im Fachunterricht
Deutsch
1. Schritt:
Die Inhaltserfassung der Bilder 1 bis 3 findet gemeinsam im Klassenverband statt, und zwar, indem exemplarisch folgendes Schema ausgefüllt wird (Arbeitsblatt):
Bild | Ort | Zeit | Personen | Handlung | Motive | Thema | Bemerk.
-----|-------|--------|----------|-------------------|--------|-------|--------
1 | | | | | | |
| | | | | | |
-----|-------|--------|----------|-------------------|--------|-------|--------
2 | | | | | | |
| | | | | | |
-----|-------|--------|----------|-------------------|--------|-------|--------
3 | | | | | | |
2. Schritt: Jetzt wird das Gruppenpuzzle organisiert.
Bilden Sie Stammgruppen zu je vier Teilnehmern. Diese sollen sich kurz zusammensetzen und sich einen Namen geben. Wie wäre es mit Namen von berühmten Naturwissenschaftlern: Kopernikus, Kepler, Brahe, Bruno, Newton, Gauß. In jeder Gruppe werden nun dieselben vier Rollen verteilt: z.B. Meister, Meisterin, Sohn und Tochter, oder auch nur die Nummern 1, 2, 3 und 4, das ist schön wissenschaftlich-abstrakt. Dieser ganze Vorgang sollte nicht länger als 10 Minuten dauern, führt aber zu klaren Zuordnungen und zu Identifikationen mit berühmten Namen: Ich Kepler 1, du Newton 3, sie Kopernikus 2.
Daraufhin bilden sich die Expertengruppen: Alle Meister (oder Einser), Meisterinnen (Zweier) usw. treffen sich, erhalten ein leeres Formblatt (wie oben) und dazu folgenden Arbeitsauftrag:
- Gruppe 1: Tragen Sie für die Bilder 4 bis 6 alle wichtigen Informationen ein.
- Gruppe 2: Tragen Sie für die Bilder 7 bis 9 alle wichtigen Informationen ein.
- Gruppe 3: Tragen Sie für die Bilder 10 bis 12 alle wichtigen Informationen ein.
- Gruppe 4: Tragen Sie für die Bilder 13 bis 15 alle wichtigen Informationen ein.
3. Schritt:
Schließlich treffen sich die Experten in Stammgruppen und tragen sich dort gegenseitig ihre Zusammenfassungen vor. Es gibt so viele Stammgruppen, wie es Teilnehmer in den Expertengruppen gab. Dadurch können Sie flexibel auf die Klassengröße reagieren.
Jetzt müsste jeder über jedes Bild informiert worden sein und jeder Schüler hat sich als Spezialist betätigt.
4. Schritt:
Formen der Auswertung und Weiterarbeit?
- a) Die Stammgruppen fügen ihre vier Formblätter - eventuell überarbeitet und verschönert - zu einem Poster zusammen und hängen dies auf.
- b) Jeder einzelne Schüler füllt jetzt für sich das obige Struktur-Diagramm aus (als Hausaufgabe). In der Stunde wird dann verglichen und ergänzt, entweder im Plenum oder wieder in den Stammgruppen.
- c) Eine Leistungsmessung findet nicht statt
(Klaus Dautel)