Individuelle Förderung im Matheunterricht: Unterschied zwischen den Versionen
UDIN (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
UDIN (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (48 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|Steckbrief| | |||
'''Klasse''': 8 | '''Klasse''': 8 | ||
| Zeile 8: | Zeile 10: | ||
'''Medienbezogene Kompetenzziele''': Sichere und eigenständige Nutzung von LearningApps und Geometrie-Software | '''Medienbezogene Kompetenzziele''': Sichere und eigenständige Nutzung von LearningApps und Geometrie-Software | ||
|Merksatz}} | |||
{{Box|Einsatz| | |||
'''Eingesetzte Tools''': GeoGebra, GeoGebra 3D | |||
☐ einmalig ☒ gelegentlich ☐ dauerhaft | |||
☐ | ☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit | ||
'''Eingesetzte Tools''': HP5-Lernlandkarte (kein Lernerfolg) | '''Eingesetzte Tools''': HP5-Lernlandkarte (kein Lernerfolg) | ||
☐ einmalig ☒ gelegentlich ☐ dauerhaft | |||
☐ | ☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit | ||
'''Eingesetzte Tools''': Anton | '''Eingesetzte Tools''': Anton | ||
☐ einmalig ☒ gelegentlich ☐ dauerhaft | |||
☐ | ☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit | ||
'''technische Voraussetzung''': Laptop/iPad: | '''technische Voraussetzung''': Laptop/iPad: | ||
| Zeile 40: | Zeile 44: | ||
*'''Lineare Funktion''': Definitionen: Terme, Gleichungen, x, Zuordnung | *'''Lineare Funktion''': Definitionen: Terme, Gleichungen, x, Zuordnung | ||
| Hervorhebung1}} | |||
{{Box|Kurzbeschreibung Projekt| | |||
In diesem Projekt wurden Schüler:innen mit einem fachlichen Förderbedarf in Kleingruppen von Studierenden betreut und individuell mit digitalen Medien gefördert. Ziel des Projekts war es, ihre fachlichen und medienbezogenen Kompetenzen zu festigen und zu erweitern. Hierfür wurden in den Einstiegsphasen das Wissen der Schüler:innen reaktiviert und bei Bedarf die vorgesehenen digitalen Tools vorgestellt. Durch variierende Sozialformen und Unterrichtsmethoden (z. B. ''Think, Pair, Share'', Expertenaustausch, Exploratives Lernen) sollten die Schüler:innen sich aktiv im Lernprozess beteiligen. Die eingesetzten digitalen Medien sollten die Schüler:innen beim Lernerfolg unterstützen und motivieren. | In diesem Projekt wurden Schüler:innen mit einem fachlichen Förderbedarf in Kleingruppen von Studierenden betreut und individuell mit digitalen Medien gefördert. Ziel des Projekts war es, ihre fachlichen und medienbezogenen Kompetenzen zu festigen und zu erweitern. Hierfür wurden in den Einstiegsphasen das Wissen der Schüler:innen reaktiviert und bei Bedarf die vorgesehenen digitalen Tools vorgestellt. Durch variierende Sozialformen und Unterrichtsmethoden (z. B. ''Think, Pair, Share'', Expertenaustausch, Exploratives Lernen) sollten die Schüler:innen sich aktiv im Lernprozess beteiligen. Die eingesetzten digitalen Medien sollten die Schüler:innen beim Lernerfolg unterstützen und motivieren. | ||
|Unterrichtsidee }} | |||
'''Skizzierung der einzelnen Einheitsschwerpunkte (60 Min. pro Einheit)''' | '''Skizzierung der einzelnen Einheitsschwerpunkte (60 Min. pro Einheit)''' | ||
<br /> | <br /> | ||
{| class="wikitable" | {| class="wikitable" | ||
|'''Einheitsschwerpunkte''' | |'''Einheitsschwerpunkte''' | ||
| Zeile 175: | Zeile 182: | ||
Gruppengespräch | Gruppengespräch | ||
|<nowiki>Arbeitsmethode</nowiki> | |||
|} | |} | ||
{{Box|Reflexion: Stärken und Schwächen| | |||
Durch den variierenden Einsatz an digitalen Tools konnte überprüft werden, welche den Lernprozess der Schüler:innen tatsächlich positiv beeinflussen. Dabei stellte sich die Lernlandkarte als weniger unterstützend heraus. Durch die kleine Gruppenkonstellation konnte individuell auf die Probleme und Bedürfnisse der Schüler:innen eingegangen und individuelle Feedbackgespräche gewährleistet werden. | |||
|Meinung}} | |||
{{Box|Beispielaufgabe| | |||
Auftrag: Erstellt eigene Erklärvideos zu einem mathematischen Inhalt, der euch | Auftrag: Erstellt eigene Erklärvideos zu einem mathematischen Inhalt, der euch interessiert. | ||
|Arbeitsmethode}} | |||
{{Box|Exemplarische O-Töne der Schüler:innen| | |||
''"Es war auf jeden Fall eine gute Methode zum Lernen. Bei meinen Fehlern, hatte ich die Wahl, entweder die Lösung zu sehen oder weiter zu Arbeiten und meine Fehler zu verbessern. Ich sah die Anton App auch zum Teil, als einen kleinen Test für mein Wissen."'' (Schüler A) | ''"Es war auf jeden Fall eine gute Methode zum Lernen. Bei meinen Fehlern, hatte ich die Wahl, entweder die Lösung zu sehen oder weiter zu Arbeiten und meine Fehler zu verbessern. Ich sah die Anton App auch zum Teil, als einen kleinen Test für mein Wissen."'' (Schüler A) | ||
| Zeile 199: | Zeile 204: | ||
''"Das wenn wir unsere aufgaben gemacht haben andere Schüler aus der Klasse da Beleidigungen drauf schreiben (auf das Jamboard) und wenn uns Herr X etwas erklären wollte andere etwas anderes machen z.B. am Handy spielen oder reden und dann frech gegenüber dem Lehrer sein."'' (Schüler D) | ''"Das wenn wir unsere aufgaben gemacht haben andere Schüler aus der Klasse da Beleidigungen drauf schreiben (auf das Jamboard) und wenn uns Herr X etwas erklären wollte andere etwas anderes machen z.B. am Handy spielen oder reden und dann frech gegenüber dem Lehrer sein."'' (Schüler D) | ||
|Zitat}} | |||
{{Box|Beispiel| | |||
[[Datei:Picture2.png|miO-Töne der ni|Beispiel: Darstellung einer Aufgabe, in der Lücken gefüllt werden müssen]] | |||
<br /> | |||
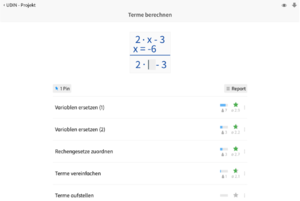
[[Datei:Picture1.png|mini|Beispiel: Darstellung einer Aufgabe, in welcher mit Termen gerechnet werden soll]] | |||
<br /> | |||
|Arbeitsmethode}} | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Prismen]] | |||
[[Kategorie:Lineare Funktion]] | |||
[[Kategorie:Terme]] | |||
[[Kategorie:Binomische Formeln]] | |||
[[Kategorie:LearningApps]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Unterrichtsidee]] | |||
[[Kategorie:Digitale Medien]] | |||
[[Kategorie:UDIN]] | |||
Aktuelle Version vom 24. April 2023, 09:11 Uhr
Klasse: 8
Unterrichtsfach: Mathematik
Thema: Prismen & Lineare Funktionen, Terme berechnen und Binomische Formeln
Fachliche Kompetenzziele: Berechnung Volumen und Oberflächeninhalt von Prismen, Anwendung binomische Formeln, Aufstellung und Berechnung von Termen und linearen Funktionsgleichungen
Medienbezogene Kompetenzziele: Sichere und eigenständige Nutzung von LearningApps und Geometrie-Software
Eingesetzte Tools: GeoGebra, GeoGebra 3D
☐ einmalig ☒ gelegentlich ☐ dauerhaft
☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit
Eingesetzte Tools: HP5-Lernlandkarte (kein Lernerfolg)
☐ einmalig ☒ gelegentlich ☐ dauerhaft
☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit
Eingesetzte Tools: Anton
☐ einmalig ☒ gelegentlich ☐ dauerhaft
☐ im Unterricht ☐ als Hausaufgabe ☒ als optionale Übung/Freiarbeit
technische Voraussetzung: Laptop/iPad:
Prismen: Geometrie-Software wie GeoGebra (online/Programm)
Lineare Funktionen: Zugangscode von den LuL damit die SuS Zugriff auf ihre Aufgaben in der Anton-App haben
Voraussetzung SuS: Umgang mit dem digitalen Endgerät, Vorwissen:
- Prismen: Definition notwendiger Begriffe (bspw.: Kanten, Ecke, Fläche, Mantelfläche, Volumen, Netze etc.);
- Lineare Funktion: Definitionen: Terme, Gleichungen, x, Zuordnung
In diesem Projekt wurden Schüler:innen mit einem fachlichen Förderbedarf in Kleingruppen von Studierenden betreut und individuell mit digitalen Medien gefördert. Ziel des Projekts war es, ihre fachlichen und medienbezogenen Kompetenzen zu festigen und zu erweitern. Hierfür wurden in den Einstiegsphasen das Wissen der Schüler:innen reaktiviert und bei Bedarf die vorgesehenen digitalen Tools vorgestellt. Durch variierende Sozialformen und Unterrichtsmethoden (z. B. Think, Pair, Share, Expertenaustausch, Exploratives Lernen) sollten die Schüler:innen sich aktiv im Lernprozess beteiligen. Die eingesetzten digitalen Medien sollten die Schüler:innen beim Lernerfolg unterstützen und motivieren.
Skizzierung der einzelnen Einheitsschwerpunkte (60 Min. pro Einheit)
| Einheitsschwerpunkte | Zeit | Unterrichtsmethoden | Sozialformen | |
| Anamnese:
Ist-Zustand bestimmen |
25m 25m
10m |
Einholen von Selbsteinschätzungen/Lehrbuchwissen Bearbeitung von Testaufgaben (think pair share)
Abgleich der Ergebnisse im Austauschverfahren |
Gruppengespräch
Einzelarbeit Partnerarbeit | |
| Digitaler Transfer:
Materiell und Personell |
10m
|
Analoge Medien, auf dem Wissensstand der Lernenden, werden wiederholt
und durch digitale Übungsmaterialien erweitert Differenzierung und Betreuung durch teil-digitalen Tandemunterricht |
Gruppengespräch
| |
| Wiederholung, Übung und Ergänzung
Digitaler Medien (ergänzt Geogebra 3D) |
15m
|
Wissensstand der Lernenden wird wiederholt
und durch digitale Übungsmaterialien erweitert
|
Gruppengespräch
| |
| Selbstgesteuertes Lernen anhand von Lernlandkarte | 15m
30m 15m |
Erklärung der Funktionsweise der Lernlandkarte
Selbstständige Aneignung Feedbackrunde mit Optimierungsvorschlägen |
Gruppengespräch
Einzelarbeit Gruppengespräch | |
| Weiteres Selbstgesteuertes Lernen anhand von Lernlandkarte | 15m
15m |
Weitere Erklärung der Funktionsweise der Lernlandkarte mit Nutzungshinweisen
Selbstständige Aneignung Feedbackrunde mit Optimierungsvorschlägen |
Gruppengespräch
Gruppengespräch | |
| Übergang der Digitalen Tools zur Anton App | 15m
30m 15m |
Erklärung der Funktionsweise der Anton App
Explorative Phase, Selbstständige Aneignung Feedbackrunde mit Optimierungsvorschlägen |
Gruppengespräch
Einzelarbeit Gruppengespräch | |
| Selbstständige Nutzung der Anton App | 5m
40m 15m |
Kurze Wissensreaktivierung der App
Explorative Phase, Selbstständige Aneignung Abschlussreflexion |
Gruppengespräch
Einzelarbeit Gruppengespräch |
Arbeitsmethode |
Durch den variierenden Einsatz an digitalen Tools konnte überprüft werden, welche den Lernprozess der Schüler:innen tatsächlich positiv beeinflussen. Dabei stellte sich die Lernlandkarte als weniger unterstützend heraus. Durch die kleine Gruppenkonstellation konnte individuell auf die Probleme und Bedürfnisse der Schüler:innen eingegangen und individuelle Feedbackgespräche gewährleistet werden.
Auftrag: Erstellt eigene Erklärvideos zu einem mathematischen Inhalt, der euch interessiert.
"Es war auf jeden Fall eine gute Methode zum Lernen. Bei meinen Fehlern, hatte ich die Wahl, entweder die Lösung zu sehen oder weiter zu Arbeiten und meine Fehler zu verbessern. Ich sah die Anton App auch zum Teil, als einen kleinen Test für mein Wissen." (Schüler A)
"Es hat mir Spaß gemacht und ich habe nebenbei auch etwas gelernt." (Schüler B)
"Man hat beim arbeiten mit der Anton App keinen Stress und man kann frei arbeiten und üben." (Schüler C)
"Das wenn wir unsere aufgaben gemacht haben andere Schüler aus der Klasse da Beleidigungen drauf schreiben (auf das Jamboard) und wenn uns Herr X etwas erklären wollte andere etwas anderes machen z.B. am Handy spielen oder reden und dann frech gegenüber dem Lehrer sein." (Schüler D)