Muster erkennen und geschickt fortsetzen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (- ZUM2Edutags) Markierung: Quelltext-Bearbeitung 2017 |
||
| (28 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{Lernpfad-Navigation| | {{Lernpfad-Navigation| | ||
[[Datei:Bienenwabe 23a.jpg|gRIFIKBERSCHREIBUNG)|200px|right]] | [[Datei:Bienenwabe 23a.jpg|gRIFIKBERSCHREIBUNG)|200px|right]] | ||
*[[ | *[[Muster erkennen und geschickt fortsetzen|Muster erkunden]] | ||
*[[ | *[[Muster erkennen und geschickt fortsetzen/Strategien beim Erkennen und Fortsetzen von Mustern|Strategien]] | ||
*[[Muster erkennen und geschickt fortsetzen/Übungsaufgaben|Übungsaufgaben]] | |||
*[[Muster erkennen und geschickt fortsetzen/Vertiefungsaufgaben|Vertiefungsaufgaben]] | |||
}} | }} | ||
}} | }} | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
{{Box|Einführung|Regelmäßige Muster findest du oft in der Natur zum Beispiel bei Pflanzen oder auch in der regelmäßigen Struktur von Bienenwaben. Aber nicht nur Tiere folgen einem festen Bauplan, auch wir bauen "Muster" in unsere Behausungen. Da überrascht es nicht, dass schon viele Mathematiker solche Muster untersuchten und mit Zahlen beschrieben. Ein besonders bekannter Mathematiker , der sich für solche Regelmäßigkeiten interessierte, war Fibonacci. Dazu werdet ihr hier später | {{Box|Einführung|Regelmäßige Muster findest du oft in der Natur zum Beispiel bei Pflanzen oder auch in der regelmäßigen Struktur von Bienenwaben. Aber nicht nur Tiere folgen einem festen Bauplan, auch wir bauen "Muster" in unsere Behausungen. Da überrascht es nicht, dass schon viele Mathematiker solche Muster untersuchten und mit Zahlen beschrieben. Ein besonders bekannter Mathematiker, der sich für solche Regelmäßigkeiten interessierte, war Fibonacci. Dazu werdet ihr hier später noch mehr entdecken! | ||
<gallery mode="packed" heights=" | <gallery mode="packed" heights="200" style="text-align:center"> | ||
Datei:Blume.jpg|'''regelmäßige Blüte''' | Datei:Blume.jpg|'''regelmäßige Blüte''' | ||
Datei:Schafsgabe.jpg|'''Schafgarbenblüten''' | Datei:Schafsgabe.jpg|'''Schafgarbenblüten''' | ||
| Zeile 19: | Zeile 20: | ||
Datei:Mauerwerk.jpg|'''Mauerwerk''' | Datei:Mauerwerk.jpg|'''Mauerwerk''' | ||
</gallery> | </gallery> | ||
|Kurzinfo}} | |||
Auf dieser ersten Seite geht es darum, regelmäßige Muster zu untersuchen. | {{Box|Was lernst du hier?| | ||
}} | Auf dieser ersten Seite geht es darum, regelmäßige Muster zu untersuchen.|Kurzinfo}} | ||
| Zeile 30: | Zeile 32: | ||
Fabian hat das folgende Muster aus Hölzchen gelegt. | Fabian hat das folgende Muster aus Hölzchen gelegt. | ||
[[Datei:Hölzchenmuster1.jpg|350px|links]] | [[Datei:Hölzchenmuster1.jpg|350px|links]] | ||
| Zeile 72: | Zeile 69: | ||
'''d)''' Berechne, wie viele Hölzer du für ein Hölzchenmuster mit einer Breite von 9 (oder 19) Hölzchen benötigst. Beschreibe wie du gerechnet hast! | |||
'''d)''' Berechne wie viele Hölzer du | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
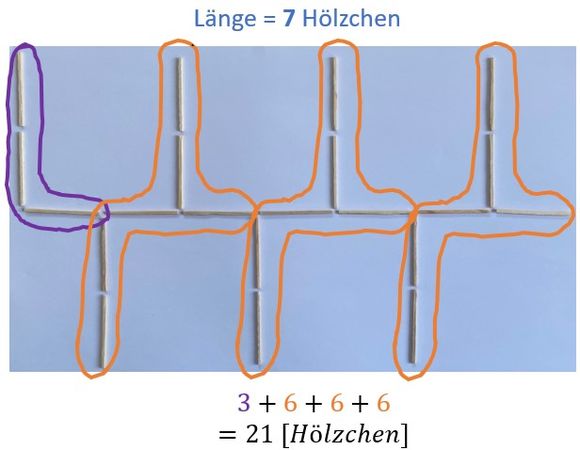
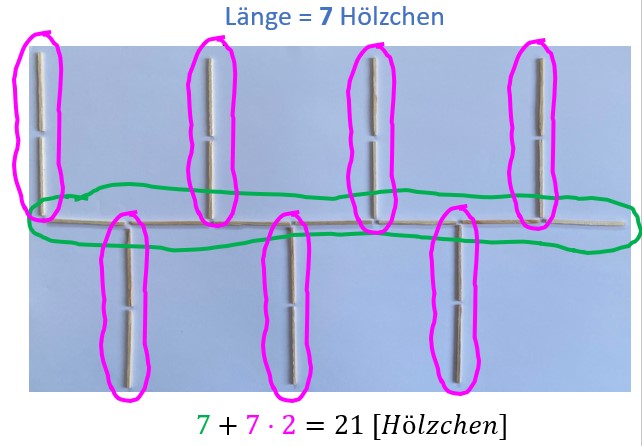
Hier kannst du dir anschauen, wie Fabian, Lucio und Merle die Hölzchen auf unterschiedliche Weise geschickt zählen. Verwende eine ähnliche Strategie, um dir zu überlegen wie viele Hölzchen du für | Hier kannst du dir anschauen, wie Fabian, Lucio und Merle die Hölzchen auf unterschiedliche Weise geschickt zählen. Verwende eine ähnliche Strategie, um dir zu überlegen wie viele Hölzchen du für ein Hölzchenmuster mit einer Breite von 9 (oder 19) Hölzchen benötigst. | ||
<gallery mode="packed" heights="300" style="text-align:center"> | <gallery mode="packed" heights="300" style="text-align:center"> | ||
| Zeile 86: | Zeile 80: | ||
</gallery> | </gallery> | ||
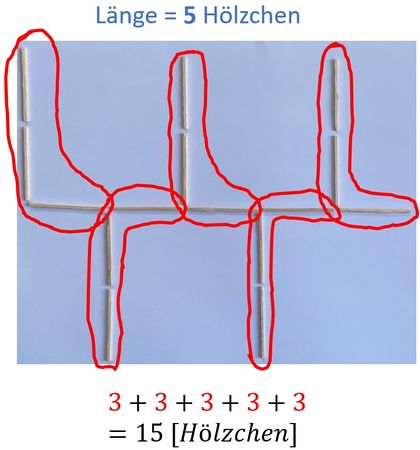
Fabian erklärt seine Strategie so: Ich sehe in dem Hölzchenmuster ganz viele L-förmige Muster. Für jedes "L" brauche ich 3 Hölzchen. Wenn ich 5 solche "L"-Muster aneinanderlege, brauche ich 3+3+3+3+3=15 Hölzchen. | Fabian erklärt seine Strategie so: Ich sehe in dem Hölzchenmuster ganz viele L-förmige Muster. Für jedes "L" brauche ich 3 Hölzchen. Wenn ich 5 solche "L"-Muster aneinanderlege, brauche ich <math>3+3+3+3+3=15</math> Hölzchen. | ||
|2=Hilfe zu Aufgabenteil d|3=Hilfe ausblenden}} | |2=Hilfe zu Aufgabenteil d|3=Hilfe ausblenden}} | ||
'''*e)''' Findest du eine Regel, wie du die Anzahl der Hölzchen für eine x-beliebige Breite des Hölzchenmusters berechnen kannst? Erkläre! | |||
{{Lösung versteckt| | |||
a-b) Hier gibt es individuelle Lösungen. Zum Vergleich findest du Beispiele für Zählstratgien von Merle, Fabian und Lucio in der Hilfe zu Aufgabenteil d) - es gibt aber noch weitere Strategien! | |||
c) Hier sind zwei Beispiele für ähnliche Bilder-Muster. Deine Lösung kann aber auch andere Muster enthalten! | |||
[[Datei:Beispiel-Bilderfolgen.jpg|500px|mitte]] | |||
d) Für eine Hölzchenmuster mit einer Breite von 9 Hölzchen brauchst du insgesamt 27 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man <math>3+3+3+...+3=27</math> oder <math>9\cdot3=27</math>. | |||
Für eine Hölzchenmuster mit einer Breite von 19 Hölzchen brauchst du insgesamt 57 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man <math>3+3+3+...+3=57</math> oder <math>19\cdot3=57</math>. | |||
e) Wenn man so zählt wie Fabian, braucht man für jedes "L" 3 Hölzchen und mit jedem solchen "L" wird das Muster ein Hölzchen breiter. Wenn man x-beliebig viele "L"-förmige Hölzchenmuster aneinanderlegt kann die Anzahl der Hölzchen so berechnen: | |||
<math> \text{Breite des ganzen Musters} \cdot 3 = \text{Anzahl der benötigten Hölzchen} </math> | |||
|Lösung zur Erkundungsaufgabe 1|Lösung ausblenden}} | |||
|Unterrichtsidee}} | |||
{{Box|Erkundungsaufgabe 2: Schokolinsenmuster| | |||
'''Merle hat Muster aus Schokolinsen gelegt. Du sollst ihr jetzt helfen die Bildmuster zu untersuchen. ''' | |||
'''a)''' Ordne die Bilder und Zahlen an die passenden Stellen in der Tabelle ein. Achtung: Einige Zahlen bleiben übrig und einige Bilder fehlen! | |||
'''Falls die App hier nicht funktioniert, findest du die App auch unter diesem Link: [https://apps.zum.de/apps/schokolinsenfolge] ''' | |||
{{H5p-zum|id=3647|height=600}} | |||
{{Lösung versteckt|Wenn du Schwierigkeiten hast die Zahlen und die Bilder zuzuordnen, zeichne dir die gesamte Bilderfolge mit Punkten in dein Heft! |Tipp zur Bearbeitung der App|Tipp ausblenden|}} | |||
'''Diese Aufgabenteile b-d beantwortest du in deinem Hefter.''' | |||
'''b)''' Beschreibe, wie sich die Bilder aus der App in Aufgabe 2a von einem Schritt zum nächsten verändern. | |||
Beschreibe, wie sich die Zahlen von Zahl zu Zahl verändern. | |||
{{Lösung versteckt|Um ihre Überlegung beim Legen der Schokolinsen zu erklären, hat Merle das Muster mit farbig sortierten Schokolinsen gelegt und für jedes Bild die Anzahl der Linsen berechnet. | |||
[[Datei:Zählstrategie Schokolinsen.jpg|400px|mitte]] | |||
|Tipp zu Aufgabenteil b|Tipp ausblenden|}} | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
<u>Beschreibung der Bilderfolge</u>) Die Bilderfolge startet mit einer Schokolinse. Im ersten Schritt werden zwei Schokolinsen hinzugelegt, sodass ein Dreieck aus drei Linsen entsteht. In jeden weiteren Schritt wird eine weitere Reihe Schokolinsen unter das Dreieck gelegt. Dabei ist jede weitere Reihe eine Schokolinse breiter als die Reihe zuvor. | |||
<u>Beschreibung der Zahlenfolge</u>) Wir starten mit der Zahl 1. Im ersten Schritt werden 2 addiert, sodass wir 3 erhalten. Im zweiten Schritt wird dazu 3 addiert, sodass wir 6 erhalten. In jeden Schritt wird eine um 1 größere Zahl addiert als im Schritt zuvor. | |||
|Lösung zu Aufgabenteil b|Lösung ausblenden|}} | |||
|Unterrichtsidee}} | |||
{{Box|Information| | |||
Anstatt die Anzahl der Schokolinsen in eine Tabelle zu schreiben, kann die Anzahl der Schokolinsen auch in einer '''Zahlenfolge''' angegeben werden. Die dritte Zahl beschreibt zum Beispiel die Anzahl der Schokolinsen im dritten Bild. In der Zahlenfolge 1, 2, 4, ... beschreibt zum Beispiel die Zahl 4, dass im dritten Bild 4 Schokolinsen gezeichnet werden müssen. | |||
|Merksatz}} | |||
{{Box|Erkundungsaufgabe 3: Von der Zahlenfolge zur Bilderfolge| | |||
'''a)''' Zeichne zu der Zahlenfolge 1, 2, 4, ... eine passende Bilderfolge und setze diese Folge noch um zwei weitere Bilder und Zahlen fort. Findest du eine weitere Möglichkeit die Folge auf andere Weise fortzusetzen? | |||
{{Lösung versteckt|Merle hat die ersten drei Bilder mit farbigen Schokolinsen gelegt. Erkennst du eine Regelmäßigkeit? | |||
[[Datei:Tipp Merle.jpg|250px|mitte]] | |||
|Tipp zu Aufgabenteil a)|Tipp ausblenden|}} | |||
{{Lösung versteckt| | |||
'''a)''' | |||
[[Datei:Stufenweise.jpg|400px|links]] | |||
| Zeile 104: | Zeile 157: | ||
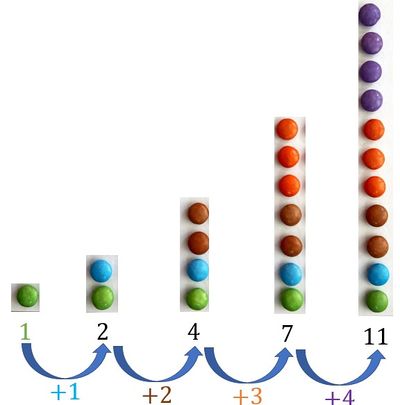
Merle hat die folgenden Bilder mit Schokolinsen gelegt und so die Zahlenfolge zu 1, 2, 4, 7, 11... ergänzt. Sie startet mit einer Schokolinse und im ersten Schritt wird eine Schokolinse hinzugelegt. In jedem weiteren Schritt wird nun eine Schokolinse mehr als im vorherigen Schritt hinzugelegt. | |||
| Zeile 114: | Zeile 168: | ||
[[Datei:Exponentielles Wachstum mit Schokolinsen.jpg|400px|links]] | |||
| | |||
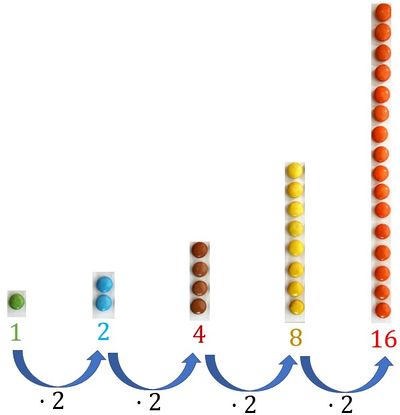
Fabian hat in der Zahlenfolge eine andere Regelmäßigkeit gesehen, als er die Bilder gelegt hat. Er startet mit einer Schokolinse und verdoppelt die Anzahl der Schokolinsen in jedem Schritt. So erhält er die Zahlenfolge 1, 2, 4, 8, 16, ... | |||
|Lösung zu Aufgabenteil a)|Lösung ausblenden|}} | |||
'''b)''' Jetzt ist deine Kreativität gefragt! Suche dir zu Hause Gegenstände in ausreichender Anzahl (zum Beispiel Süßigkeiten, Geschirr, Stifte, Murmeln, ...). Lege mit diesen Gegenständen eine Bilderfolge und mache ein Foto. Notiere auch die dazugehörige Zahlenfolge. Gelingt es dir mit den Gegenständen auch eine weitere, noch schwieriger zu erkennende Bilderfolge zu legen? | |||
|Unterrichtsidee}} | |||
{{Fortsetzung|weiter=Übersicht über Strategien beim geschickten Fortsetzen von Mustern|weiterlink=Muster erkennen und geschickt fortsetzen/Strategien beim Erkennen und Fortsetzen von Mustern}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Lernpfad]] | |||
Aktuelle Version vom 17. Dezember 2021, 08:22 Uhr
Regelmäßige Muster findest du oft in der Natur zum Beispiel bei Pflanzen oder auch in der regelmäßigen Struktur von Bienenwaben. Aber nicht nur Tiere folgen einem festen Bauplan, auch wir bauen "Muster" in unsere Behausungen. Da überrascht es nicht, dass schon viele Mathematiker solche Muster untersuchten und mit Zahlen beschrieben. Ein besonders bekannter Mathematiker, der sich für solche Regelmäßigkeiten interessierte, war Fibonacci. Dazu werdet ihr hier später noch mehr entdecken!
Diese Aufgabe beantwortest du in deinem Hefter.
Fabian hat das folgende Muster aus Hölzchen gelegt.
a) Wie viele Hölzchen siehst du? Beschreibe, wie du beim Zählen vorgegangen bist!
b) Findest du auch eine weitere geschickte Zählstrategie? Notiere deine Rechnung!
c) Lucio hat ein ähnliches Muster gelegt. Zeichne beide Muster in dein Heft und ergänze mindestens zwei weitere ähnliche Muster. Wie viele Hölzchen brauchst du für die Muster jeweils?
d) Berechne, wie viele Hölzer du für ein Hölzchenmuster mit einer Breite von 9 (oder 19) Hölzchen benötigst. Beschreibe wie du gerechnet hast!
Hier kannst du dir anschauen, wie Fabian, Lucio und Merle die Hölzchen auf unterschiedliche Weise geschickt zählen. Verwende eine ähnliche Strategie, um dir zu überlegen wie viele Hölzchen du für ein Hölzchenmuster mit einer Breite von 9 (oder 19) Hölzchen benötigst.
*e) Findest du eine Regel, wie du die Anzahl der Hölzchen für eine x-beliebige Breite des Hölzchenmusters berechnen kannst? Erkläre!
a-b) Hier gibt es individuelle Lösungen. Zum Vergleich findest du Beispiele für Zählstratgien von Merle, Fabian und Lucio in der Hilfe zu Aufgabenteil d) - es gibt aber noch weitere Strategien!
c) Hier sind zwei Beispiele für ähnliche Bilder-Muster. Deine Lösung kann aber auch andere Muster enthalten!
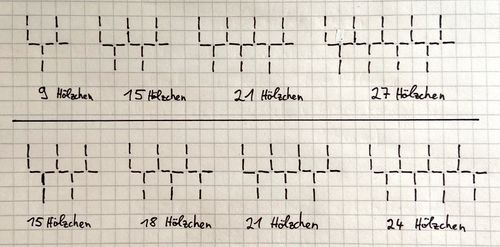
d) Für eine Hölzchenmuster mit einer Breite von 9 Hölzchen brauchst du insgesamt 27 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man oder .
Für eine Hölzchenmuster mit einer Breite von 19 Hölzchen brauchst du insgesamt 57 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man oder .
e) Wenn man so zählt wie Fabian, braucht man für jedes "L" 3 Hölzchen und mit jedem solchen "L" wird das Muster ein Hölzchen breiter. Wenn man x-beliebig viele "L"-förmige Hölzchenmuster aneinanderlegt kann die Anzahl der Hölzchen so berechnen:
Merle hat Muster aus Schokolinsen gelegt. Du sollst ihr jetzt helfen die Bildmuster zu untersuchen.
a) Ordne die Bilder und Zahlen an die passenden Stellen in der Tabelle ein. Achtung: Einige Zahlen bleiben übrig und einige Bilder fehlen!
Falls die App hier nicht funktioniert, findest du die App auch unter diesem Link: [1]
Diese Aufgabenteile b-d beantwortest du in deinem Hefter.
b) Beschreibe, wie sich die Bilder aus der App in Aufgabe 2a von einem Schritt zum nächsten verändern.
Beschreibe, wie sich die Zahlen von Zahl zu Zahl verändern.
Um ihre Überlegung beim Legen der Schokolinsen zu erklären, hat Merle das Muster mit farbig sortierten Schokolinsen gelegt und für jedes Bild die Anzahl der Linsen berechnet.
Beschreibung der Bilderfolge) Die Bilderfolge startet mit einer Schokolinse. Im ersten Schritt werden zwei Schokolinsen hinzugelegt, sodass ein Dreieck aus drei Linsen entsteht. In jeden weiteren Schritt wird eine weitere Reihe Schokolinsen unter das Dreieck gelegt. Dabei ist jede weitere Reihe eine Schokolinse breiter als die Reihe zuvor.
Beschreibung der Zahlenfolge) Wir starten mit der Zahl 1. Im ersten Schritt werden 2 addiert, sodass wir 3 erhalten. Im zweiten Schritt wird dazu 3 addiert, sodass wir 6 erhalten. In jeden Schritt wird eine um 1 größere Zahl addiert als im Schritt zuvor.
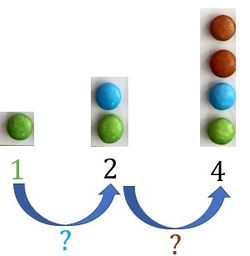
Anstatt die Anzahl der Schokolinsen in eine Tabelle zu schreiben, kann die Anzahl der Schokolinsen auch in einer Zahlenfolge angegeben werden. Die dritte Zahl beschreibt zum Beispiel die Anzahl der Schokolinsen im dritten Bild. In der Zahlenfolge 1, 2, 4, ... beschreibt zum Beispiel die Zahl 4, dass im dritten Bild 4 Schokolinsen gezeichnet werden müssen.
a) Zeichne zu der Zahlenfolge 1, 2, 4, ... eine passende Bilderfolge und setze diese Folge noch um zwei weitere Bilder und Zahlen fort. Findest du eine weitere Möglichkeit die Folge auf andere Weise fortzusetzen?
a)
Merle hat die folgenden Bilder mit Schokolinsen gelegt und so die Zahlenfolge zu 1, 2, 4, 7, 11... ergänzt. Sie startet mit einer Schokolinse und im ersten Schritt wird eine Schokolinse hinzugelegt. In jedem weiteren Schritt wird nun eine Schokolinse mehr als im vorherigen Schritt hinzugelegt.
Fabian hat in der Zahlenfolge eine andere Regelmäßigkeit gesehen, als er die Bilder gelegt hat. Er startet mit einer Schokolinse und verdoppelt die Anzahl der Schokolinsen in jedem Schritt. So erhält er die Zahlenfolge 1, 2, 4, 8, 16, ...
b) Jetzt ist deine Kreativität gefragt! Suche dir zu Hause Gegenstände in ausreichender Anzahl (zum Beispiel Süßigkeiten, Geschirr, Stifte, Murmeln, ...). Lege mit diesen Gegenständen eine Bilderfolge und mache ein Foto. Notiere auch die dazugehörige Zahlenfolge. Gelingt es dir mit den Gegenständen auch eine weitere, noch schwieriger zu erkennende Bilderfolge zu legen?