Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Benutzer:Funktionen-Sprache: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
(Die Seite wurde neu angelegt: „=Funktionen - Sprache= Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben. {{Lösung v…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben. | Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben. | ||
| Zeile 49: | Zeile 49: | ||
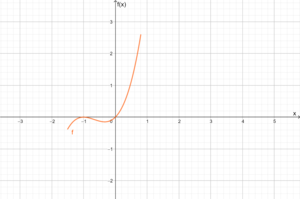
# <math>D =</math>[-1,5;0,8] <math>W = </math> [-0,2 ; 2,6] | # <math>D =</math>[-1,5;0,8] <math>W = </math> [-0,2 ; 2,6] | ||
|Lösung zeigen|Lösung verstecken}}|Lösung}} | |Lösung zeigen|Lösung verstecken}}|Lösung}} | ||
{{button | |||
|position=links | |||
|text=Funktion - eine eindeutige Zuordnung <span class="fa fa-chevron-circle-right"></span> | |||
|link=Benutzer: Funktion - eine eindeutige Zuordnung | |||
}} | |||
{{button | |||
|position=links | |||
|text=Funktion - eine eindeutige Zuordnung <span class="fa fa-chevron-circle-right"></span> | |||
|link=Benutzer: Einführung von Funktionen | |||
}} | |||
Aktuelle Version vom 26. März 2020, 13:39 Uhr
Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.
- Die Funktionen-Sprache kennen und anwenden können.
- Die Funktionen-Sprache in Anwendungsbeispiele interpretieren können.
- Formeln im Hinblick auf funktionale Aspekte untersuchen können.
- Definitions- und Wertemenge einer Funktion bestimmen können.
- FA 1.4: Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im Kontext deuten können.
- FA 1.7: Funktionen als mathematische Modelle verstehen und damit verständig arbeiten können.
Um den "Gültigkeitsbereich" einer Funktion anzugeben, verwendet man folgende Begriffe:
Definitions- und Wertemenge
Alle Werte, die die unabhängige Variable (Argument) annimmt, bilden zusammen die Definitionsmenge D der Funktion. Alle Werte, die die abhängige Variable annimmt, bilden die Wertemenge W
Bezeichnungen bei Funktionen
- Die Elemente der Definitionsmenge D einer Funktion nennt man Argumente oder Stellen der Funktion.
- Die Elemente der Wertemenge W nennt man Funktionswerte der Funktion.
- f(x) ist der Funktionswert der Funktion f an der Stelle x.
- Der Graph der Funktion f besteht aus den Punkten (x / f(x)).
Funktionenschreibweise
- Funktion mit ist eine normalerweise verwendete Funktionsschreibweise.
- Auch mit ist üblich.
- "f" ist der Funktionsname. Für den Funktionsnamen verwendet man üblicherweise (nicht zwingend) Kleinbuchstaben.
- "2x - 3" ist der Funktionsterm der Funktion f.
- Die Schreibweise legt für die Funktion f als Grundmenge und als Zielmenge fest. Die Zielmenge gibt an, in welcher Menge die Funktionswerte der Funktion f liegen können. Die Wertemenge ist immer eine Teilmenge der Zielmenge. Die Grundmenge gibt an, in welcher Menge die Argumente der Funktion f liegen können. Die Definitionsmenge ist immer Teilmenge der Grundmenge.
- Ist die Definitionsmenge und Wertemenge einer Funktion eine Teilmenge von so spricht man von einer reellen Funktion. Wenn nicht anders angegeben, handelt es sich um reelle Funktionen.
Lösung
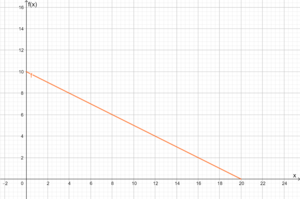
- D = [0 ; 20] W = [0 ; 10]
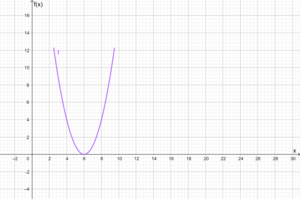
- D = [2,5 ; 9,5] W = [0 ; 12,1]
Lösung