Zentrische Streckung/Abbildung durch zentrische Streckung/3.Station: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 7: | Zeile 7: | ||
==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ||
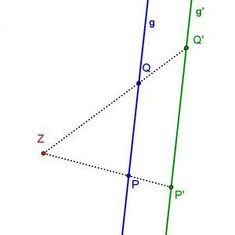
{{Box|1= Wie wird die Strecke <math> \overline{PQ} </math> im Verhältnis zu gestreckt|2= | |||
Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.<br> | Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.<br> | ||
Geometrisch bedeutet dies für einen beliebigen Punkt P: <math> \overline{ZP'} = \mid k\mid \cdot \overline{ZP}</math><br> | Geometrisch bedeutet dies für einen beliebigen Punkt P: <math> \overline{ZP'} = \mid k\mid \cdot \overline{ZP}</math><br> | ||
| Zeile 22: | Zeile 24: | ||
<math>\Rightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ ('''<span style="text-decoration: overline;">ZQ</span>''' - '''<span style="text-decoration: overline;">ZP</span>''')<br> | <math>\Rightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ ('''<span style="text-decoration: overline;">ZQ</span>''' - '''<span style="text-decoration: overline;">ZP</span>''')<br> | ||
<math>\Rightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ '''<span style="text-decoration: overline;">PQ</span>''' | <math>\Rightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ '''<span style="text-decoration: overline;">PQ</span>''' | ||
|} | |3=Arbeitsmethode}} | ||
<br> | <br> | ||
[[Bild:Porzelt_lobenderPanto3.jpg]] | [[Bild:Porzelt_lobenderPanto3.jpg]] | ||
Version vom 18. August 2019, 17:50 Uhr
3. Station: Berechnung der Streckenlängen und des Streckungsfaktors
k
