Nullstellen bestimmen/Faktorisieren von Polynomen

Nullstellen bestimmen

• Überblick
• Ausklammern
• Faktorisieren von Polynomen
• Vielfachheit von Nullstellen am Graph erkennen
• Erraten von Nullstellen
• Substitution

< zurück zu Mathematik-digital.de

Worum geht's?

Wie du schon in Station 2 gelernt hast, ist es zur Nullstellenbestimmung (und nicht nur da!) günstig, wenn man ein Polynom in faktorisierter Form angeben kann. Dann kann man nämlich die Nullstellen oft einfach ablesen. In dieser Station lernst du ein Verfahren kennen, wie du Polynome faktorisieren kannst, wenn Ausklammern nicht möglich ist. Nicht schlecht, oder? ;)

Informiere dich!

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Theorie - intensiv studieren!

Hole am Pult das Arbeitsblatt zu dieser Station. Es enthält alle wichtigen Informationen zusammengefasst. Studiere den Text intensiv und versuche alles möglichst gut zu verstehen. Du musst im Anschluss daran Fragen dazu beantworten!

Zerlegungssatz

Faktorisieren

Verstanden, worum es geht?

In diesem Quiz kannst du zeigen, ob du das Arbeitsblatt verstanden hast... ;)

In diesem Quiz musst du dem faktorisierten Term seine Nullstellen zuordnen. Mehrfache Nullstellen sind auch dabei! :)

Übung macht den Meister

Aufgabe

Bestimme in deinem Heft in äußerst übersichtlicher Form die Nullstellen x₁ und x₂ der Funktion und gib die faktorisierte Form an.

$f(x)=x^2-4x+3$

$f(x)=(x-1)(x-3)$

$f(x)=\frac{1}{2}x^2 -2x$

$f(x)=0,5x(x-4)$

$f(x)=2x^2+4x-6$

$f(x)=2(x+3)(x-1)$

Faktorsiere und kürze. Achte auf formale Richtigkeit beim kürzen! $f(x)=\frac{x^3-5x^2}{(x-1)^2\cdot(x-5)}$

$f(x)=\frac{x^3-5x^2}{(x-1)^2\cdot(x-5)}=\frac{x^2}{(x-1)^2}$ für x ungleich 5

Weitere Aufgaben findest du im Buch auf S.145/2

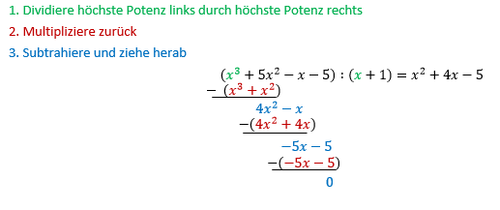
Polynomdivision

Sind nicht alle Nullstellen des Polynoms bekannt, so musst kannst du nicht sofort alles faktorisieren.
Kennst du aber zumindest eine Nullstelle, kannst du mit dem Verfahren der Polynomdivsion Schritt für Schritt weitere Nullstellen finden und so immer weiter faktorisieren.


Hör dir den überragenden Polynomdivisionssong an und verinnerliche das Prinzip gut. Im Anschluss musst du sie selbst durchführen.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Hole dir das Arbeitsblatt vom Pult und vollziehe die Polynomdivision noch einmal gut durch.

AB Polynomdivision

Teste dich!

Übung

Führe in deinem Heft die Polynomdivision durch.
Weitere Aufgaben findest du im Buch auf S.145/5

$(x^3+5x^2-x-5):(x+1)$

$(4x^2+12x+5):(2x+1)$

$2x+5$

$(3x^3-x^2-3x+1):(x-1)$

$3x^2+2x-1$

$(x^3+x^2-8x+4):(x-2)$

$x^2+3x-2$

für Experten
$(x^5-1):(x-1)$

$x^4+x^3+x^2+1$

$(3x^3-8x^2+x+2):(x^2-2x-1)$

$3x+2$

Abschlussübung

Übung

Füge all dein neu erworbenes Wissen zusammen und bestimme die Nullstellen der folgenden Funktion und gib die Funktion vollständig faktorisiert an.
$f(x)=x^3-2x^2-4x+8$, wenn $x=2$ als Nullstelle bekannt ist.

$f(x)=(x+2)(x-2)^2$ mit einfacher Nullstelle $x_1=-2$ und doppelter Nullstelle bei $x_(2,3)=2$

Das war nicht ohne...! Zum Abschluss noch etwas eher Entspannendes, nämlich das "Erraten" der ersten Nullstelle, damit man die Polynomdivision überhaupt durchführen kann!

Weiter