Zentrische Streckung/Abbildung durch zentrische Streckung/2.Station Fortsetzung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 49: Zeile 49:
{{{!}} class="wikitable"
{{{!}} class="wikitable"
{{!}}-
{{!}}-
! k !! <span style="color:#ff6600"><math>\overline{ZB}</math></span> !! <span style="color:#660000"><span style="text-decoration: overline;">ZB'</span></span>
! k !! <span style="color:#ff6600"><math>\overline{ZB}</math></span> !! <span style="color:#660000"><math>\overline{ZB^{'}</math></span>
{{!}}- style="background-color:#00ff00"
{{!}}- style="background-color:#00ff00"
{{!}} 2 {{!}}{{!}} 4 {{!}}{{!}} 8  
{{!}} 2 {{!}}{{!}} 4 {{!}}{{!}} 8  
{{!}}- style="background-color:#00ff00"
{{!}}- style="background-color:#ffff00"
{{!}} 1.5 {{!}}{{!}} 4 {{!}}{{!}} 6  
{{!}} 1.5 {{!}}{{!}} 4 {{!}}{{!}} 6  
{{!}}- style="background-color:#00ff00"
{{!}}- style="background-color:#EE00ee"
{{!}} 1 {{!}}{{!}} 4 {{!}}{{!}} 4  
{{!}} 1 {{!}}{{!}} 4 {{!}}{{!}} 4  
{{!}}- style="background-color:#00ff00"
{{!}}- style="background-color:#436eee"
{{!}} 0.5 {{!}}{{!}} 4 {{!}}{{!}} 2
{{!}} 0.5 {{!}}{{!}} 4 {{!}}{{!}} 2
{{!}}- style="background-color:#00ff00"
{{!}}- style="background-color:#cfcfcf"
{{!}} 0 {{!}}{{!}} 4 {{!}}{{!}} 0
{{!}} 0 {{!}}{{!}} 4 {{!}}{{!}} 0
{{!}}}
{{!}}}


{{!}
{!} width ="60px" {!} &nbsp;
{!}{!}
{{!} {{Prettytable}}
{!}-
! k !! <span style="color:#ff6600"><span style="text-decoration: overline;">ZB</span></span> !! <span style="color:#660000"><span style="text-decoration: overline;">ZB'</span></span>
{!}- style="background-color:#00ff00"
! 2 !! 4 !! 8
{!}- style="background-color:#ffff00"
! 1.5 !! 4 !! 6
{!}- style="background-color:#EE00ee"
! 1 !! 4 !! 4
{!}- style="background-color:#436eee"
! 0.5 !! 4 !! 2
{!}- style="background-color:#cfcfcf"
! 0 !! 4 !! 0
{!}}


{!}{!}


{{!} {{Prettytable}}
{{{!}} class="wikitable"
{!}-  
{{!}}-
! k !! <span style="color:#ff6600"><span style="text-decoration: overline;">ZB</span></span> !! <span style="color:#660000"><span style="text-decoration: overline;">ZB'</span></span>
! k !! <span style="color:#ff6600"><math>\overline{ZB}</math></span> !! <span style="color:#660000"><math>\overline{ZB^{'}</math></span>
{!}- style="background-color:#00ff00"
{{!}}- style="background-color:#00ff00"
! -2 !! 4 !! 8
{{!}} -2 {{!}}{{!}} 4 {{!}}{{!}} 8  
{!}- style="background-color:#ffff00"
{{!}}- style="background-color:#ffff00"
! -1.5 !! 4 !! 6
{{!}} -1.5 {{!}}{{!}} 4 {{!}}{{!}} 6  
{!}- style="background-color:#EE00ee"
{{!}}- style="background-color:#EE00ee"
! -1 !! 4 !! 4
{{!}} -1 {{!}}{{!}} 4 {{!}}{{!}} 4  
{!}- style="background-color:#436eee"
{{!}}- style="background-color:#436eee"
! -0.5 !! 4 !! 2
{{!}} -0.5 {{!}}{{!}} 4 {{!}}{{!}} 2
{!}- style="background-color:#cfcfcf"
{{!}}- style="background-color:#cfcfcf"
! 0 !! 4 !! 0
{{!}} -0 {{!}}{{!}} 4 {{!}}{{!}} 0
{!}}
{{!}}}
{!}}
 




Version vom 29. Mai 2019, 12:27 Uhr


Abbildungen durch zentrische Streckung
Porzelt Streckenlänge.jpg
  1. Ähnlichkeitsabbildungen
  2. Streckungsfaktor
  3. Berechnung der Streckenlängen und des Streckungsfaktors
  4. Zusammenfassung
  5. Übung
  6. Wissenswertes


Fortsetzung der 2. Station: Streckungsfaktor

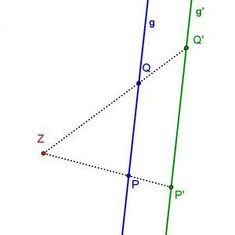
Bei dieser zentrischen Streckung musst du dir anschauen, wie sich die Streckenlängen verändern, wenn du k veränderst. Lass dir dafür die Streckenlängen anzeigen!
Was verändert sich? Orientiere dich dabei an den unter dem Applet stehenden Fragen! Überlege genau, denn es können mehrere Antworten richtig sein!

GeoGebra

1 Wie lang ist ZB', wenn k = 2 ist?

ZB' ist 8 LE lang.
ZB' ist 6 LE lang.
ZB' ist 4 LE lang.

2 Wie lang ist ZB, wenn k = -1 ist?

ZB ist 4 LE lang.
ZB ist 6 LE lang.
ZB ist 8 LE lang.

3 Wie lang ist ZB', wenn k = 3 ist?

ZB' ist 12 LE lang.
ZB' ist 6 LE lang.
ZB' ist 8 LE lang.

4 Für welches k ist ZB' = 6 LE lang?

Für k = 1,5.
Für k = -1,5.
Für k = 2.
Für k = -2,5.


Die Werte, die sich aus der Änderung von k ergeben, wurden in zwei Tabellen zusammengefasst. In der linken sind die Werte für k von 2 bis 0, in der rechten für k von -2 bis 0.

Analysiere die Tabellen

Betrachte die Tabellen und überlege dir, wie sich die Länge von ZB' im Vergleich zur Länge von ZB in Abhängigkeit von k ändert!

k Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \overline{ZB^{'}}
2 4 8
1.5 4 6
1 4 4
0.5 4 2
0 4 0


k Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \overline{ZB^{'}}
-2 4 8
-1.5 4 6
-1 4 4
-0.5 4 2
-0 4 0


ist -mal so lang wie .

Hier siehst du was das k bedeutet. Merke es dir, denn später wirst du darüber abgefragt!

Merke
k bezeichnet man als den Streckungsfaktor. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.

Porzelt lobenderPanto2.jpg

Berechnung der Streckenlängen und des Streckungsfaktors
Abgerufen von „https://unterrichten.zum.de/index.php?title=Zentrische_Streckung/Abbildung_durch_zentrische_Streckung/2.Station_Fortsetzung&oldid=95406“