Benutzer:Cloehner/Stochastik Einführungsphase NRW/Zufallsgrößen - Wahrscheinlichkeitsverteilungen - Erwartungswerte: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Box|Übergreifende Aufgabe|Erstelle auf Basis der Ergebnisse aller Aufgaben dieser Seite ein Produkt, aus dem die Bedeutung der eingeführten Fachbegriffe sowie die Vorgehensweise zur Berechnung neu eingeführter Werte hervorgeht. Entscheide selbst, in welcher Form du die Inhalte aufbereiten möchtest (z.B. in Textform, als Sketchnote, als Präsentation, ...) | |||
<span class="fa fa-group fa-2x"></span> Du darfst diese Aufgabe alleine oder in einer Gruppe von maximal vier Personen bearbeiten.|Hervorhebung1}} | |||
| Zeile 5: | Zeile 10: | ||
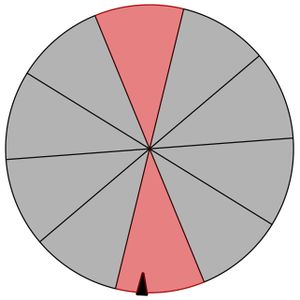
Klara bietet auf einem Straßenfest ein Glücksspiel an. Das abgebildete Glücksrad wird dreimal gedreht. Wird bei jeder Drehung ein graues Feld getroffen, so verliert man seinen Einsatz von 1,00 €. Wenn bei den drei Drehungen genau einmal ein rotes Feld getroffen wird, wird 1,50 € ausgezahlt, bei zweimal „rot” wird 2,50 € ausgezahlt und bei dreimal „rot” beträgt die Auszahlungssumme 5 €. | Klara bietet auf einem Straßenfest ein Glücksspiel an. Das abgebildete Glücksrad wird dreimal gedreht. Wird bei jeder Drehung ein graues Feld getroffen, so verliert man seinen Einsatz von 1,00 €. Wenn bei den drei Drehungen genau einmal ein rotes Feld getroffen wird, wird 1,50 € ausgezahlt, bei zweimal „rot” wird 2,50 € ausgezahlt und bei dreimal „rot” beträgt die Auszahlungssumme 5 €. | ||
==Die Wahrscheinlichkeiten der verschiedenen Gewinnsummen== | |||
{{Aufgaben|1|Stelle das dreimalige Drehen des Glücksrades in einem Baumdiagramm dar.}} | {{Aufgaben|1|Stelle das dreimalige Drehen des Glücksrades in einem Baumdiagramm dar.}} | ||
{{Aufgaben|2| | {{Aufgaben|2|Lege eine Tabelle an, in der du in der oberen Zeile die möglichen '''Gewinnsummen''' und darunter die '''Wahrscheinlichkeit''', mit der die entsprechende Gewinnsumme erzielt wird, zusammenstellst. Du kannst dein Ergebnis überprüfen, indem du die Werte in die folgende Tabelle einträgst. Alle Werte, die nach einem Klick auf "Prüfen" stehen bleiben, sind korrekt.}} | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 23: | Zeile 31: | ||
| style="padding:5px" | '''0,512|64/125()''' | | style="padding:5px" | '''0,512|64/125()''' | ||
| style="padding:5px" | '''0,384|48/125()''' | | style="padding:5px" | '''0,384|48/125()''' | ||
| style="padding:5px" |'''0,096|12/125()''' | | style="padding:5px" | '''0,096|12/125()''' | ||
| style="padding:5px" |'''0,008|1/125()''' | | style="padding:5px" | '''0,008|1/125()''' | ||
|} | |} | ||
</div> | </div> | ||
{{Aufgaben|3|Informiere dich über die Bedeutung der Begriffe '''diskrete Zufallsgröße''' und '''Wahrscheinlichkeitsverteilung'''. | |||
''Zur Wahrscheinlichkeitsverteilung auf die Wahrscheinlichkeits- und die Verteilungsfunktion verwiesen. Beide würden an dieser Stelle jedoch zu weit führen.}} | |||
Erläutere, inwiefern dir auf dieser Seite bereits eine diskrete Zufallsgröße und eine Wahrscheinlichkeitsverteilung begegnet sind. Beachte mit Blick auf das übergreifende Produkt, welches du zu dieser Seite erstellen sollst insbesondere auch Formelzeichen und Schreibweisen wie <math>X</math> , <math>x_i (x_1,x_2,...)</math> und <math>P(X=...)</math>. | |||
<span class="fa fa-exclamination-circle fa-2x"></span> Eine '''Erläuterung''' geht deutlich über eine reine Zuordung der Begriffe heraus. Die Bedeutung der beiden Begriffe soll in dieser Aufgabe exemplarisch verdeutlicht werden!}} | |||
==Handelt es sich um ein faires Spiel?== | |||
Natürlich kann man bei einem Glücksspiel nicht immer gewinnen. Dennoch lassen sich Kriterien definieren, anhand derer man entscheiden kann, ob das Spiel fair gestaltet ist. | |||
{{Aufgaben|4|Formuliere Bedingungen, unter denen du ein Glücksspiel als fair bezeichnen würdest.}} | |||
{{Aufgaben|5|Angenommen das Glücksspiel wird 1000-mal durchgeführt. Wie oft sind die verschiedenen Gewinnsummen dabei im Idealfall zu erwarten? | |||
Berechne auf Basis der vorhergesagten absoluten Häufigkeiten das arithmetische Mittel der Gewinnsummen. | |||
{{Lösung versteckt|Nach dem Gesetz der großen Zahlen nähern sich die relativen Häufigkeiten der Ausgänge eines Glücksspiels bei sehr großer Versuchsanzahl immer weiter den theoretischen Wahrscheinlichkeiten an.|Tipp 1 anzeigen|Tipp 1 ausblenden}} | |||
{{Lösung versteckt|Nach 1000 Runden können als Schätzwert für die relativen Häufigkeiten der verschiedenen Gewinnsummen die Wahrscheinlichkeiten aus Aufgabe 2 verwendet werden. Berechne daraus die gesuchten absoluten Häufigkeiten.|Tipp 2 anzeigen|Tipp 2 ausblenden}} | |||
{{Lösung versteckt|Nach 1000 Versuchen hat man im Schnitt ein Gewinn von -144,00 € gemacht.|Kontrolllösung anzeigen|Kontrolllösung ausblenden}} | |||
}} | |||
Version vom 25. April 2019, 22:04 Uhr
Klara bietet auf einem Straßenfest ein Glücksspiel an. Das abgebildete Glücksrad wird dreimal gedreht. Wird bei jeder Drehung ein graues Feld getroffen, so verliert man seinen Einsatz von 1,00 €. Wenn bei den drei Drehungen genau einmal ein rotes Feld getroffen wird, wird 1,50 € ausgezahlt, bei zweimal „rot” wird 2,50 € ausgezahlt und bei dreimal „rot” beträgt die Auszahlungssumme 5 €.
Die Wahrscheinlichkeiten der verschiedenen Gewinnsummen
| Gewinnsumme: | -1,00|-1() € | 0,50|0,5() € | 1,50|1,5() € | 4,00|4() € |
| Wahrscheinlichkeit: | 0,512|64/125() | 0,384|48/125() | 0,096|12/125() | 0,008|1/125() |
Informiere dich über die Bedeutung der Begriffe diskrete Zufallsgröße und Wahrscheinlichkeitsverteilung.
Zur Wahrscheinlichkeitsverteilung auf die Wahrscheinlichkeits- und die Verteilungsfunktion verwiesen. Beide würden an dieser Stelle jedoch zu weit führen.
Erläutere, inwiefern dir auf dieser Seite bereits eine diskrete Zufallsgröße und eine Wahrscheinlichkeitsverteilung begegnet sind. Beachte mit Blick auf das übergreifende Produkt, welches du zu dieser Seite erstellen sollst insbesondere auch Formelzeichen und Schreibweisen wie , und .
Eine Erläuterung geht deutlich über eine reine Zuordung der Begriffe heraus. Die Bedeutung der beiden Begriffe soll in dieser Aufgabe exemplarisch verdeutlicht werden!}}
Handelt es sich um ein faires Spiel?
Natürlich kann man bei einem Glücksspiel nicht immer gewinnen. Dennoch lassen sich Kriterien definieren, anhand derer man entscheiden kann, ob das Spiel fair gestaltet ist.
Angenommen das Glücksspiel wird 1000-mal durchgeführt. Wie oft sind die verschiedenen Gewinnsummen dabei im Idealfall zu erwarten?
Berechne auf Basis der vorhergesagten absoluten Häufigkeiten das arithmetische Mittel der Gewinnsummen.