main>Nina Krämer |
main>Nina Krämer |
| Zeile 33: |
Zeile 33: |
|
| |
|
| Im Folgenden werden aber nur noch quantitative Merkmale betrachtet. | | Im Folgenden werden aber nur noch quantitative Merkmale betrachtet. |
| ==== Info ====
| | |
| Nicht immer macht es Sinn, alle verschiedenen Merkmalsausprägungen einzeln zu betrachten. Bei quantitativen Merkmalen fasst man oft verschiedene Merkmalsausprägungen zu Klassen zusammen. | | Nicht immer macht es Sinn, alle verschiedenen Merkmalsausprägungen einzeln zu betrachten. Bei quantitativen Merkmalen fasst man oft verschiedene Merkmalsausprägungen zu Klassen zusammen. |
|
| |
|
Version vom 7. April 2015, 22:00 Uhr
Man kann jede Art von Merkmalen klassieren. Das geht sogar bei qualitativen Merkmalen mit einer Nominalskala.
| Beispiel Merkmal Lieblingsfarbe
|
Sind zum Beispiel die Farben hellgelb, gelb, sonnengelb, rot, grün, hellblau, mittelblau, himmelblau und dunkelblau unter den Merkmalsausprägungen, so könnte man die Klassen
- "gelb" mit den Merkmalsausprägungen hellgelb, gelb und sonnengelb,
- "blau" mit den Merkmalsausprägungen hellblau, mittelblau, himmelblau und dunkelblau ,
- "Andere" mit den verbliebenden Merkmalsausprägungen bilden.
Dies wird auch bei der Auswertung von Wahlergebnissen im Fernsehen gemacht, die kleineren, nicht so wichtigen Parteien werden unter "Andere" zusammengefasst.
|
Bei qualitativen Merkmalen mit einer Ordinalskala wird man immer darauf achten, dass aufeinander folgende Merkmalsausprägungen zusammengefasst werden.
| Beispiel Merkmal Note Mathematikarbeit
|
Betrachtet man die Noten der letzten Mathematikarbeit, so könnte man die Klassen
- "Leistungsträger" für die Merkmalsausprägungen "sehr gut" und "gut",
- "Mittelfeld" für die Merkmalsausprägungen "befriedigend" und "ausreichend" und
- "Blauer Brief" für die Merkmalsausprägungen "mangelhaft" und "ungenügend" bilden,
um eine knappe Übersicht über die Lerngruppe zu erhalten.
|
Im Folgenden werden aber nur noch quantitative Merkmale betrachtet.
Nicht immer macht es Sinn, alle verschiedenen Merkmalsausprägungen einzeln zu betrachten. Bei quantitativen Merkmalen fasst man oft verschiedene Merkmalsausprägungen zu Klassen zusammen.
| Beispiel Körpergröße (in cm)
Betrachtet man zum Beispiel die Körpergröße (in cm) der Schüler und Schülerinnen der Klasse HHU5 am Berufskolleg Hattingen (Schuljahr 2012/2013):
Urliste
| Körpergröße in cm
|
| 170 |
178 |
174 |
188 |
168
|
| 191 |
169 |
159 |
199 |
200
|
| 177 |
178 |
200 |
193 |
169
|
| 151 |
185 |
191 |
165 |
158
|
| 185 |
188 |
194 |
180 |
170
|
Wenn man hier die verschiedenen Merkmalsausprägungen mit ihren absoluten und relativen Häufigkeiten erfasst, ist noch nicht wirklich etwas gewonnen, da es 18 verschiedene Merkmalsausprägungen gibt, von denen sieben die absolute Häufigkeit 2 und alle anderen die absolute Häufigkeit 1 haben. (Der geneigte Leser mag das selber nachrechnen.)
Man könnte zum Beispiel die Frage "Wie viele Schüler sind größer als 175 cm und höchstens 183 cm? stellen.
Dann ist es sinnvoll, eine absolute Häufigkeitsverteilung mit drei verschiedenen Klassen zu bilden. Jede Klasse hat eine untere und eine obere Grenze. Wichtig ist, dass sich die Klassen nicht überschneiden, damit jeder Beobachtungswert nur genau zu einer Klasse gehört.
|
|
Klasseneinteilung:
Klasse  : :
- vom kleinsten Wert
 (hier: 151 cm) bis zu 175 cm einschließlich (hier: 151 cm) bis zu 175 cm einschließlich
- mathematische Kurzschreibweise:
![{\displaystyle [151;175]=]150;175]}](/index.php?title=Spezial:MathShowImage&hash=576947e69dfb1046992537c0d029a944&mode=mathml)
Klasse  : :
- von über 175 cm bis zu 183 cm einschließlich
- mathematische Kurzschreibweise:
![{\displaystyle ]175;183]}](/index.php?title=Spezial:MathShowImage&hash=5879d427309341e71ac70313ac05076c&mode=mathml)
Klasse  : :
- von über 183 cm bis zum größten Wert
 (hier 200 cm) einschließlich (hier 200 cm) einschließlich
- mathematische Kurzschreibweise:
![{\displaystyle ]183;200]}](/index.php?title=Spezial:MathShowImage&hash=b03e40881647633ffa8d00892567212a&mode=mathml)
Häufigkeitsverteilung bestimmen:
Jetzt kann man die absolute Häufigkeit  zu jeder Klasse zu jeder Klasse  bestimmen, indem man alle Beobachtungswerte zählt, die im Intervall der Klasse bestimmen, indem man alle Beobachtungswerte zählt, die im Intervall der Klasse  liegen.
Dann lässt sich auch die relative Häufigkeit liegen.
Dann lässt sich auch die relative Häufigkeit  zu jeder Klasse zu jeder Klasse  bestimmen, indem man den Anteil aller Beobachtungswerte am Stichprobenumfang bestimmen, indem man den Anteil aller Beobachtungswerte am Stichprobenumfang  , die im Intervall der Klasse , die im Intervall der Klasse  liegen, berechnet. liegen, berechnet.
| Klassierte Körpergrößen HHU5 2012/2013
|
 |
 |
 |
 |
Summe
|
 |
 |
 |
 |

|
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{2}{5}=40 %}
|
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{4}{25}=16 %}
|
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{11}{25}=44 %}
|
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100 %}
|
|
|
Interpretation:
Es sind also nicht nur vier Schüler größer als 175 cm und höchstens 183 cm. Es sieht so aus, als wären die Schüler der Klasse entweder klein oder groß, weil die Klasse in der Mitte so selten vertreten ist.
Stimmt das denn?
Hier ist es hilfreich, sich mit den Klassenbreiten zu beschäftigen.
Klassenbreiten bestimmen:
Die gewählten Klassen  sind unterschiedlich breit. Die Breite sind unterschiedlich breit. Die Breite  einer Klasse einer Klasse  errechnet man, indem man die untere Grenze errechnet man, indem man die untere Grenze  von der oberen Grenze von der oberen Grenze  subtrahiert. subtrahiert.
Klasse  |
untere Grenze  |
obere Grenze  |
Klassenbreite 
|
 |
 |
 |

|
 |
 |
 |

|
 |
 |
 |

|
|
|
Jetzt sieht man, dass die mittlere Klasse auch viel schmaler ist, als die beiden anderen Klassen. Die Klassenbreite hat aber Einfluss auf die Häufigkeit, mit der die Beobachtungswerte in der Klasse liegen. Deshalb wählt man in der Regel Klassen mit gleicher Klassenbreite. Nur in Ausnahmefällen machen Klassen mit unterschiedlichen Klassenbreiten Sinn. Ganz besonders gut geeignet sind unterschiedliche Klassenbreiten, wenn man schon vorher weiß, welche Aussage man mit den Daten unterstützen möchte.
Auch die obige Fragestellung hätte man prima mit gleich breiten Klassen lösen können. Dabei beginnt man dann mit dem aus der Frage vorgegebenen Intervall und bildet alle nötigen Klassen darunter und darüber mit Klassenbreite 8 cm so, dass man auch den kleinsten und den größten Beobachtungswert einer Klasse zuordnen kann.
Das sieht dann so aus:
| Klassierte Körpergrößen HHU5 2012/2013
|
Klasse  |
Intervall |
 |

|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{1}{25}=4 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{2}{25}=8 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{1}{25}=4 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{6}{25}=24 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{4}{25}=16 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{6}{25}=24 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{3}{25}=12 %}
|
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{2}{25}=8 %}
|
| Summe |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%}
|
|
| Interpretation:
|
|
Man kann leicht erkennen, dass es - unter Berücksichtigung der Klassenbreite - nur zwei Klassen gibt, in denen sich mehr Beobachtungswerte befinden. So erhält man also ein ganz anderes Bild der Verteilung.
|
Merke
Wenn bei einer umfangreichen Stichprobe sehr viele unterschiedliche Merkmalsausprägungen auftreten, so bietet es sich an, ähnliche Werte in sogenannte
Klassen 
der
(Klassen-)Breite 
zusammenzufassen.
Man unterscheidet zwei Arten von Klassenbildungen:
- Klassen mit gleicher Klassenbreite

- Klassen mit unterschiedlicher Klassenbreite

Übrigens eignen sich Klassen mit unterschiedlicher Klassenbreite hervorragend, um Daten so aufzubereiten, dass sie die gewünschte Aussage (hier entweder eine Klasse mit besonders großen Schülern oder mit besonders kleinen Schülern) gut unterstützen. Hier gilt der allseits beliebte Spruch: "Traue keiner Statistik, die du nicht selbst gefälscht hast."
Klassen mit gleicher Klassenbreite
Für die Anzahl der Klassen gilt die folgende Regel,
wobei  der Stichprobenumfang ist:
der Stichprobenumfang ist:

| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist
 . .
Also gilt für die Anzahl der Klassen
 . .
|
Eine Klasse ist ein Teil der Spannweite  (
( für Range,dem englischen Begriff für Spannweite), also ein Teil der Differenz zwischen der größten Merkmalsausprägung
für Range,dem englischen Begriff für Spannweite), also ein Teil der Differenz zwischen der größten Merkmalsausprägung  und der kleinsten Merkmalsausprägung
und der kleinsten Merkmalsausprägung  .
.
| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist
 und und , ,
somit gilt für die Spannweite
 . .
|
Die Klassenbreite  ist der Quotient aus Spannweite und Klassenanzahl.
ist der Quotient aus Spannweite und Klassenanzahl.
| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist die Klassenbreite also
 . .
|
Bei der Zuordnung der Merkmalsausprägungen ist darauf zu achten, dass sich die Klassen nicht überschneiden. Sonst könnte es passieren, dass eine Merkmalsausprägung zwei Klassen zugeordnet wird.
Beachten Sie:
Wählen Sie einen geeigneten Startwert als untere Klassengrenze (die in der Regel nicht zur Klasse gehören sollte) der ersten Klasse, addieren Sie die Klassenbreite um die obere Klassengrenze (diese gehört zur Klasse) zu erhalten.
Die obere Klassengrenze der vorangegangenen Klasse wird die untere Grenze der nächsten Klasse.
Und so fährt man fort, bis alle Klassen definiert sind.
Merke
Die einzelnen Klassen bezeichnet man mit  , wobei
, wobei 
 gilt.
gilt.
Klassenanzahl:

Spannweite:

Klassenbreite:

|
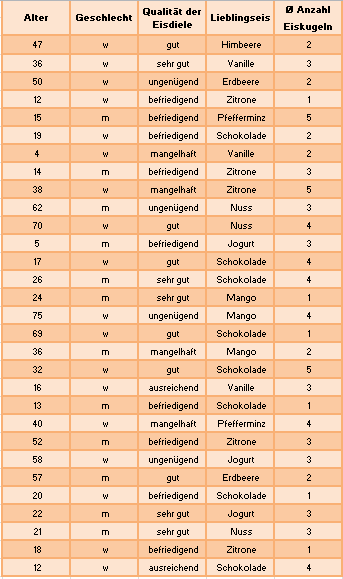
Einführungsbeispiel - Teil 6.1
Bei der Umfrage der Eisdiele "Rabe" weist das Merkmal "Alter" sehr viele verschiedene Merkmalsausprägungen (genau 28 verschiedene Merkmalsausprägungen) auf, so dass eine Aufbereitung nach absoluten oder relativen Häufigkeitsverteilungen nicht zu mehr Übersicht beitragen würde. Hier bietet es sich an, Klassen zu bilden, um die Altersstruktur der Kunden besser zu verstehen.
| Größe |
Formel |
im Beispiel mit |
Einsetzen und Berechnen
|
| Klassenanzahl |
 \sqrt{n}</math> \sqrt{n}</math> |
 |
 
|
| Spannweite |
  |
 und und  |
 
|
| Klassenbreite |
 |
 und und  |
 
|
|
| Jetzt geht es an die Klassenbildung:
Legt man fest, dass die untere Grenze selbst nicht zur Klasse gehört, aber die obere Grenze der Klasse dazugehört, so hat man sichergestellt, dass die Beobachtungswerte den Klassen eindeutig zugeordnet werden können.
Dann wählt man einen Startwert für die untere Grenze der ersten Klasse  und addiert dann für die obere Klassengrenze die Klassenbreite zum Startwert. Die jeweils nächste Klasse hat dann als untere Grenze die obere Grenze der vorangegangenen Klasse. und addiert dann für die obere Klassengrenze die Klassenbreite zum Startwert. Die jeweils nächste Klasse hat dann als untere Grenze die obere Grenze der vorangegangenen Klasse.
Wählt man den Startwert  , so erhält man die Klassen , so erhält man die Klassen  mit mit  : :
![{\displaystyle k_1=]0;13], k_2=]13;26], k_3=]26;39],}](/index.php?title=Spezial:MathShowImage&hash=adc46e6da67e16b53551baab131911cf&mode=mathml) ![{\displaystyle k_1=]39;52], k_2=]52;65], k_3=]65;78]}](/index.php?title=Spezial:MathShowImage&hash=02691f577939f3b0f4569740df650e04&mode=mathml)
|
|
Einführungsbeispiel - Teil 6.2
Jetzt muss die absolute Häufigkeit ermittelt werden, mit der die Beobachtungswerte in den einzelnen Klassen liegen:
| Klassen |
Häufigkeiten
|
Klasse  |
über ... Jahre |
bis zu ... Jahre |
 |
 |
 in Prozent in Prozent
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 16,7%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 36,7%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 13,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 13,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 10,0%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 10,0%}
|
| Summe |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%}
|
|
| Interpretation
Auffällig ist, dass mehr als ein Drittel aller Kunden zwischen 13 und 26 Jahren alt sind. Der Besitzer der Eisdiele könnte hieraus zum Beispiel ableiten, dass er mehr Angebote für die anderen Altersklassen anbieten sollte, um auch für diese Gruppen attraktiv zu sein und so mehr Umsatz zu erzielen.
Ausblick
Selbstverständlich wäre es auch möglich, eine andere Klassenanzahl zu wählen und so zu anderen Ergebnissen zu gelangen. Es ist nicht zwingend, die obigen Formeln für die Klassenanzahl und Klassenbreite zu wählen. Sie bieten aber einen guten Anhaltspunkt für eine erste Auswertung.
Hier noch eine weitere Auswertung mit 8 Klassen und einer Klassenbreite von 10.
| Klassen |
Häufigkeiten
|
Klasse  |
über ... Jahre |
bis zu ... Jahre |
 |
 |
 in Prozent in Prozent
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 6,7%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 33,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 13,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 16,7%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 6,7%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 10,0%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 10,0%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 3,3%}
|
| Summe |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%}
|
|
Klassen mit beliebiger Klassenbreite
Und noch einmal die Eisdiele "Rabe":
|
Einführungsbeispiel - Teil 7
Auch bei der Auswertung des Merkmals Alter kann man mit unterschiedlich großen Klassenbreiten arbeiten und versuchen zu interessanten Aussagen zu gelangen.
Wählt man beispielsweise nur zwei Klassen, die erste von 0 - 30 Jahre, die zweite von 30 - 80 Jahre, so erhält man:
| Klassen |
Häufigkeiten
|
Klasse  |
über ... Jahre |
bis zu ... Jahre |
 |
 |
 in Prozent in Prozent
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 53,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 46,7%}
|
| Summe |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%}
|
|
| Interpretation
Auf den ersten Blick sieht es so aus, als sei die Eisdiele bei jeder Altersgruppe gleich beliebt. Dies ist jedoch nicht so, wie man im Abschnitt Klassen mit gleicher Klassenbreite gut sehen konnte.
Noch ein Versuch:
Diesmal wählt man drei Klassen und erhält:
| Klassen |
Häufigkeiten
|
Klasse  |
über ... Jahre |
bis zu ... Jahre |
 |
 |
 in Prozent in Prozent
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 23,3%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 30%}
|
 |
 |
 |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 46,7%}
|
| Summe |
 |
 |
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%}
|
|
| Interpretation
Hier könnte man auf den ersten Blick folgern, dass die Eisdiele "Rabe" gerade beim älteren Publikum besonders angesagt ist.
|
Bleiben noch zwei Hinweise, die man beachten sollte:
Merke
Bei Klassen mit unterschiedlichen Breiten ist jeder Klasse  ihre Breite
ihre Breite  zuzuordnen
zuzuordnen
Vorsicht bei Statistiken mit unterschiedlich breiten Klassen. Hier weiß man nie, was der Autor verstecken will.
Hier geht's weiter Übungen Klassenbildung
zurück zu Grundbegriffe der beschreibenden Statistik




