Beschreibende Statistik/Merkmal und Merkmalsausprägungen: Unterschied zwischen den Versionen
main>Matthias Scharwies K (Matthias Scharwies verschob Seite Beschreibende Statistik/Grundbegriffe der beschreibenden Statistik/Merkmal und Merkmalsausprägungen nach Beschreibende Statistik/Grundbegriffe/Merkmal und Merkmalsausprägungen) |
main>Matthias Scharwies K (Matthias Scharwies verschob Seite Beschreibende Statistik/Grundbegriffe/Merkmal und Merkmalsausprägungen nach Beschreibende Statistik/Merkmal und Merkmalsausprägungen, ohne dabei eine Weiterleitung anzulegen) |
Version vom 15. April 2019, 08:23 Uhr
Beispiel Umfrage vor der Bundestagswahl 2013
|
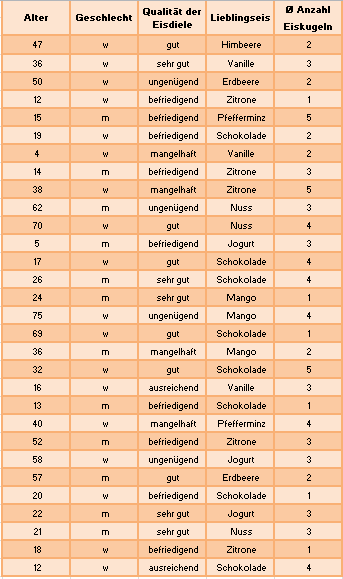
Vor der Bundestagswahl 2013 wurden 1000 Wahlberechtigte befragt, welche Partei sie wählen möchten und wie alt sie sind. Die erhobenen Daten wurden in einer Urliste (Ausschnitt: siehe rechts) erfasst. Man bezeichnet "Alter" und "Partei" als Merkmal. Jedes Merkmal hat verschiedene Merkmalsausprägungen. Zum Beispiel hat das Merkmal "Alter" die Merkmalsausprägungen "20", "18" und "37". Das Merkmal "Partei" hat die Merkmalsausprägungen "Grüne", "CDU" und "SPD". Selbstverständlich gibt es noch jeweils weitere Merkmalausprägungen. Jeder der Befragten ist im Hinblick auf die Merkmale "Alter" und "Partei" ein Merkmalsträger. | |||||||||||||||||||
Wie immer in der Mathematik kommt man auch hier nicht ohne mathematische Definitionen aus.
Jede in einer statistischen Erhebung untersuchte Frage heißt Merkmal.
Die einzelnen Antworten heißen Beobachtungswerte und werden getrennt nach Merkmalen in einer Urliste festgehalten. Die Beobachtungswerte werden mit bezeichnet.
Die Anzahl aller Beobachtungswerte ist gleich dem Stichprobenumfang .
Zu einer Stichprobe vom Umfang gibt es in der zugehörigen Urliste die Beobachtungswerte .
Die verschiedenen Werte die ein Merkmal annimmt, werden Merkmalsausprägungen genannt und mit bezeichnet. Es kann höchstens so viele Merkmalsausprägungen geben, wie es Beobachtungswerte in der Urliste gibt. In der Regel wird die Anzahl der Merkmalsausprägungen kleiner sein als der Stichprobenumfang. Die zu einem Merkmal gehörenden Ausprägungen werden mit bezeichnet.
Jedes Element der Stichprobe einer statistischen Erhebung ist ein Merkmalsträger bezogen auf die untersuchten Merkmale.
|
Einführungsbeispiel - Teil 3 Die erhobenen Daten werden in einer Urliste zusammengefasst. Jeder befragte Kunde ist im Hinblick auf die Merkmale „Alter“, „Geschlecht“, „Qualität der Eisdiele“, „Lieblingseis“ und „Durchschnittliche Anzahl der gegessenen Eiskugeln“ ein Merkmalsträger. Die Anzahl der Merkmalsträger nennt man Stichprobenumfang (hier ). Die Merkmale selbst kommen in verschiedenen Ausprägungen vor: | ||
| Merkmal | Merkmalsausprägungen | Kommen alle Merkmalsausprägungen vor? |
|---|---|---|
| Alter | 0; 1; 2;...;100 | nein |
| Geschlecht | m, w | ja |
| Qualität der Eisdiele | sehr gut, gut, befriedigend, ausreichend, mangelhaft, ungenügend | ja |
| Lieblingseis | Himbeere, Vanille, Erdbeere, Pfefferminz, Schokolade, Zitrone, Mango, Jogurt, Nuss | ja |
| Durchschnittliche Anzahl der gegessenen Eiskugeln | 1, 2, 3, 4, 5 | ja |
|
Betrachtet man das Merkmal "Geschlecht" so lauten die Beobachtungswerte Es gibt Beobachtungswerte , aber nur zwei verschiedene Merkmalsausprägungen . Jetzt legt man (beliebig) fest:
| ||
| Noch ein Beispiel |
|---|
|
Die Urliste zum Merkmal "Alter der Lerngruppe" hat einen Stichprobenumfang von und enthält folgende Beobachtungswerte: Dann bezeichnet man die Beobachtungswerte so: Sortiert man die Urliste zum Merkmal "Alter der Lerngruppe" der Größe nach, so erhält man eine sortierte Urliste: Aus dieser sortierten Urliste lassen sich leicht die einzelnen Merkmalsausprägungen ablesen. Das Merkmal "Alter der Lerngruppe" hat Merkmalsausprägungen Man bezeichnet die Merkmalsausprägungen so: Diese mathematischen Schreibweisen werden im Folgenden noch häufiger verwendet und ist sehr nützlich, wenn es darum geht, etwas allgemein zu formulieren. |