Trigonometrische Funktionen/Einfluss von b: Unterschied zwischen den Versionen
K (Kilian Schoeller verschob die Seite Trigonometrische Funktionen 2/Einfluss von b nach Trigonometrische Funktionen/Einfluss von b, ohne dabei eine Weiterleitung anzulegen) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | |||
===FAQ=== | ===FAQ=== | ||
[[Trigonometrische_Funktionen | [[Trigonometrische_Funktionen/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | ||
===Einfluss von b=== | ===Einfluss von b=== | ||
Wir betrachten nun den Einfluss von <math> \ b </math> in | Wir betrachten nun den Einfluss von <math> \ b </math> in | ||
| Zeile 14: | Zeile 11: | ||
{{ | {{Box|1=Aufgabe B1|2= | ||
<ggb_applet height="350" width="400" type="button" filename="sin_b.ggb" /><br> | <ggb_applet height="350" width="400" type="button" filename="sin_b.ggb" /><br> | ||
| Zeile 21: | Zeile 18: | ||
# Überlege dir, wie sich die Werte <math> \ b = 3 </math> und <math> \ b = -1 </math> sowie <math> \ b = 0,5 </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | # Überlege dir, wie sich die Werte <math> \ b = 3 </math> und <math> \ b = -1 </math> sowie <math> \ b = 0,5 </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | ||
# Formuliere das Ergebnis deiner Untersuchungen. <br> | # Formuliere das Ergebnis deiner Untersuchungen. <br> | ||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
{{Box|1=Merke|2= | |||
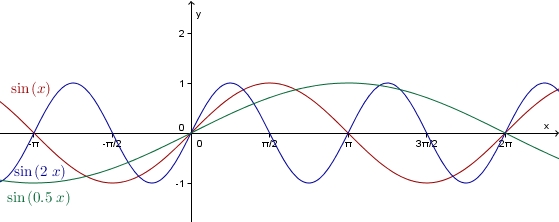
Man erhält den Graph der Funktion | |||
:<math> x \rightarrow \sin ( b\cdot x ) </math> | |||
aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der <math>\ x</math>-Achse. Genauer: | |||
* <span style="background-color:yellow;"> Ist der Betrag von <math>\ b</math> größer als eins, so wird der Graph der Sinusfunktion in <math>\ x</math>-Richtung mit dem Faktor Betrag von <math> \frac{1}{b} </math> gestaucht. | |||
* <span style="background-color:yellow;"> Ist der Betrag von <math>\ b</math> kleiner als eins, so wird der Graph der Sinusfunktion in <math>\ x</math>-Richtung mit dem Faktor Betrag von <math> \frac{1}{b} </math> gestreckt. | |||
* <span style="background-color:yellow;"> Falls <math> \ b </math> negativ ist, so wird der Graph zusätzlich an der <math>\ y</math>-Achse gespiegelt. | |||
Die Periode der Funktion ist <math>\frac{2\pi}{|b|}</math>.</span> | |||
D.h., wenn man z.B. <math>\ b </math> verdoppelt, so halbiert sich die Periode. |3=Merksatz}} | |||
[[Bild:N_sin_b.jpg|center]] | |||
}} | }} | ||
{{Box|1=Aufgabe B2|2= | |||
{{ | |||
Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen! | Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen! | ||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig. | |||
Eine mögliche formale Begründung: | |||
:Es gilt: | |||
::<math>\sin(x)=\sin\left(b\cdot\frac{x}{b}\right)</math> | |||
:Dies bedeutet, dass die Funktion <math> x \rightarrow \sin ( b\cdot x ) </math> schon an der Stelle <math>\frac{x}{b}</math> den Funktionswert von <math> x \rightarrow \sin (x ) </math> annimmt. | |||
}} | }} | ||
{{Box|1=Aufgabe B3|2= | |||
{{ | |||
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! | Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 62: | Zeile 77: | ||
</quiz> | </quiz> | ||
|3=Arbeitsmethode}} | |||
Nun betrachten wir den Einfluss von <math> \ b </math> in | Nun betrachten wir den Einfluss von <math> \ b </math> in | ||
:<math> x \rightarrow \cos ( b\cdot x ) </math>. | :<math> x \rightarrow \cos ( b\cdot x ) </math>. | ||
{{ | {{Box|1=Aufgabe B4|2= | ||
<ggb_applet height="350" width="400" type="button" filename="cos_b.ggb" /><br> | <ggb_applet height="350" width="400" type="button" filename="cos_b.ggb" /><br> | ||
Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe B1 noch einmal für <math>cos</math>. | Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe B1 noch einmal für <math>cos</math>. | ||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
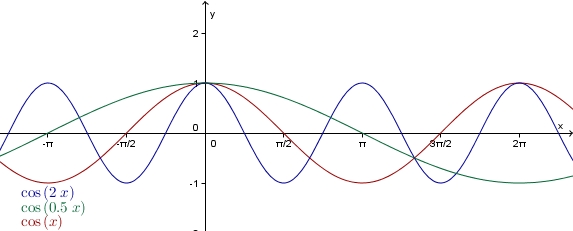
Die allgemeine Kosinusfunktion verhält sich bei Variation von <math> \ b </math> genauso wie die allgemeine Sinusfunktion. | |||
[[Bild:N_cos_b.jpg|center]] | |||
}} | }} | ||
---- | ---- | ||
<span style="background-color:yellow;">Hefteintrag:</span> Beachte, dass in der Lösung zur Aufgabe B1 ein Hefteintrag "versteckt" ist! | |||
---- | ---- | ||
{{Weiter|Trigonometrische Funktionen/Einfluss der Parameter|Zurück zu Station 1: Einfluss der Parameter}} | |||
Version vom 10. Oktober 2018, 13:52 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von b
Wir betrachten nun den Einfluss von in
- .
Die Datei [INVALID] wurde nicht gefunden.
- Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von ändern.
- Stelle den Schieberegler auf ein. Wie ändert sich der Graph?
- Überlege dir, wie sich die Werte und sowie auf den Graphen auswirken und überprüfe deine Vermutung.
- Formuliere das Ergebnis deiner Untersuchungen.
Man erhält den Graph der Funktion
aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der -Achse. Genauer:
- Ist der Betrag von größer als eins, so wird der Graph der Sinusfunktion in -Richtung mit dem Faktor Betrag von gestaucht.
- Ist der Betrag von kleiner als eins, so wird der Graph der Sinusfunktion in -Richtung mit dem Faktor Betrag von gestreckt.
- Falls negativ ist, so wird der Graph zusätzlich an der -Achse gespiegelt.
Die Periode der Funktion ist .
D.h., wenn man z.B. verdoppelt, so halbiert sich die Periode.
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig.
Eine mögliche formale Begründung:
- Es gilt:
- Dies bedeutet, dass die Funktion schon an der Stelle den Funktionswert von annimmt.
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen!
Nun betrachten wir den Einfluss von in
- .
Die Datei [INVALID] wurde nicht gefunden.
Die allgemeine Kosinusfunktion verhält sich bei Variation von genauso wie die allgemeine Sinusfunktion.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe B1 ein Hefteintrag "versteckt" ist!