Figuren im Koordinatensystem

Lernpfad

Thema Bilder und Figuren im Koordinatensystem

Dieser Lernpfad soll eine erste Einführung in das Arbeiten im Koordinatensystem liefern.

Schatzsuche

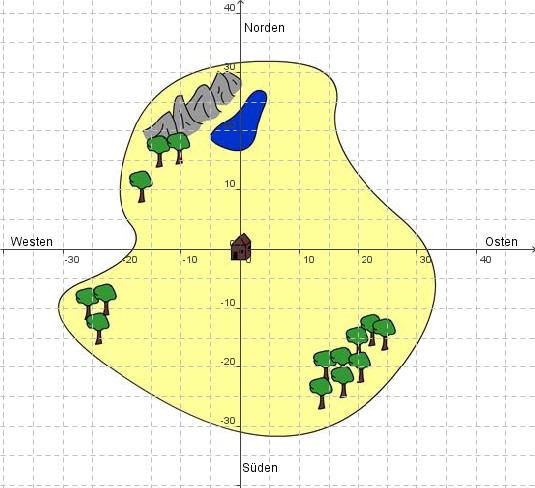
Käpt'n Flint möchte seinen alten Piratenschatz, den er vor Jahren auf der Insel Goldirum vergraben hat, zurückholen. Da er selbst zu alt für die Sache ist, gibt er seinen beiden treuesten Matrosen folgende Anweisung:

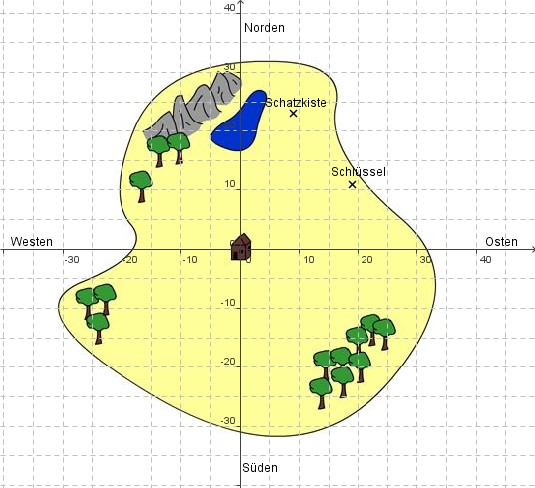
Ihr geht zunächst zur Hütte der verlassenen Geister, die sich gut sichtbar genau in der Mitte der Insel befindet. Joe, du wirst den Schlüssel der Schatzkiste suchen. Du findest ihn, wenn du von der Hütte aus zunächst 19 Meter nach Osten und dann 11 Meter nach Norden gehst. Und du, Jim, suchst die Schatztruhe. Dafür musst du erst 9 Meter nach Osten und dann 23 Meter nach Norden gehen.

Findest du den Schlüssel und die Schatztruhe?

Das Koordinatensystem

Hier siehst du ein Koordinatensystem, in das der Punkt A eingetragen wurde:

Merke

Punkte im Koordinatensystem kann man durch zwei Zahlen (die wir dann Koordinaten nennen) beschreiben. Wichtig ist dabei der "Null-Punkt" (der Ursprung) des Koordinatensystems. Damit ist derjenige Punkt gemeint, an dem sich die beiden Achsen schneiden.

Wollen wir nun z.B. einen Punkt mit der ersten Koordinate 7 (die erste Koordinate nennen wir x-Koordinate) und der zweiten Koordinate 3 (diese heißt y-Koordinate) in das Koordinatensystem eintragen, so gehen wir vom Ursprung aus erst 7 Einheiten nach rechts und dann 3 Einheiten nach oben. Wir schreiben dann P(7/3).

Weitere Tipps: Koordinaten ablesen mit Karopapier und ohne, Punkte bei gegebenen Koordinaten auf Karopapier eintragen und ohne.

Aufgabe 1

Im Bild siehst du rechts die Koordinaten von 6 zufällig erzeugten Punkten. Oben sind die Punkte A bis F, aber sie sind noch an der falschen Stelle. Unten rechts gibt es eine Checkbox, mit der du dir die richtige Position anzeigen lassen kannst. Zeige Sie aber nur an, wenn du fertig oder zu unsicher bist.

Wenn du fertig bist, kannst du noch einmal mit neuen Punkten üben, indem du die zwei Pfeile rechts oben im Bild anklickst.

Aufgabe 2

Kannst du Koordinaten ablesen? Auf dem folgenden Arbeitsblatt kannst du es überprüfen.

Bilder im Koordinatensystem

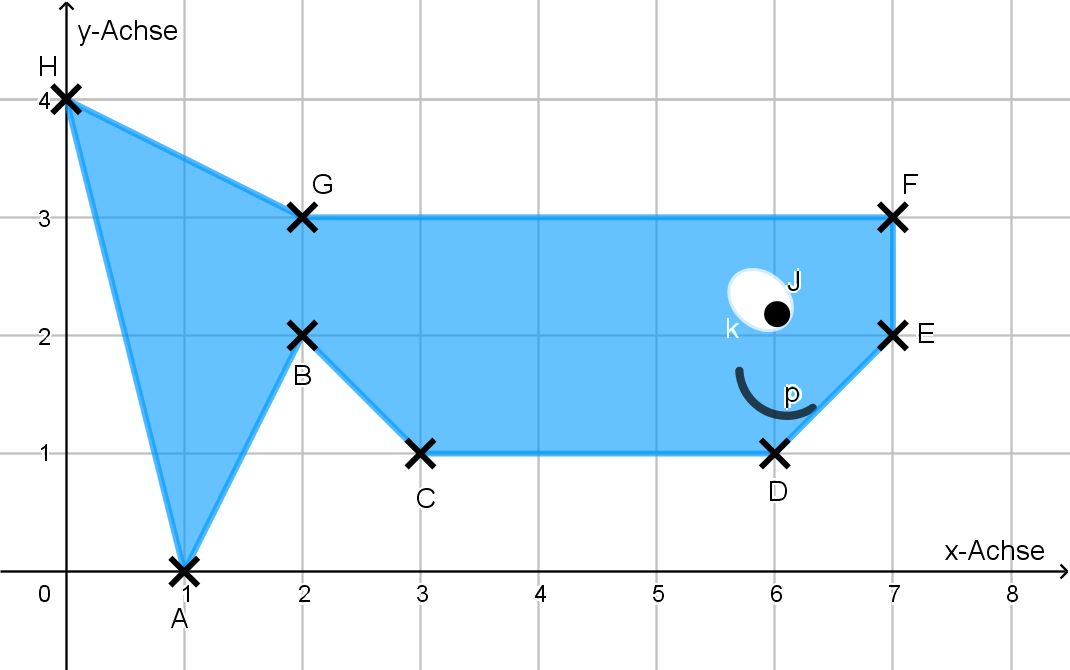
Mit Hilfe von Koordinaten kann man auch Bilder beschreiben. Unten siehst du einen Fisch im Koordinatensystem (das wird noch genauer erklärt). Du kannst den Fisch zeichnen, wenn du die Koordinaten der Punkte A, B ..., H kennst.

Geogebra-Applet fehlt! Name war früher Koordinatensystemfisch.ggb von Birgit Lachner

Aufgabe 3

Lies die Koordinaten der Punkte A, B ..., H ab.

A(2/1), B(3/2), C(4/1), D(6/1), E(7/2), F(6/3), G(4/3), H(2/3)

Aufgabe 4

Verändere die Figur nun so, dass die Punkte A, B ..., H folgende Koordinaten haben:

A(1/1), B(2/2), C(3/1), D(6/1), E(7/2), F(7/3), G(3/3), H(1/3)

Aufgabe 5

Trage die folgenden Punkte in ein Koordinatenystem ein und verbinde sie in alphabetischer Reihenfolge: A(3/1), B(5/1), C(7/3), D(7/10), E(6/11), F(3/11), G(2/10), H(2/8), I(3/8), J(3/7), K(2/7), L(2/6), M(1/6), N(1/5), O(2/5), P(2/4), Q(4/5), R(2/3), S(2/2), T(3/1)

Benutze hierfür die  Koordinatensytemvorlage.

Wenn du fertig bist, kannst du das Bild, das nun entstanden ist, noch nach deinen eigenen Vorstellungen vervollkommnen.

Aufgabe 6

Übertrage die vier Figuren so in ein Koordinatensystem, dass der Punkt J auf der x-Achse liegt und der Punkt K die Koordinaten (16/3) hat. Gib die Koordinaten aller Punkte an.

A(1/1), B(7/1), C(7/4), D(1/4), E(4/5), F(6/7), G(4/9), H(2/7), J(12/0), K(16/3), L(8/5), M(8/6), N(14/6), O(16/9), P(10/9)

Aufgabe 7

Besondere Lage im Koordinatensystem: Was haben alle Punkte gemeinsam, wenn sie ... ? Hier einige Beispiele, dass Punkte manchmal Gemeinsamkeiten haben, wenn sie eine bestimmte Position zueinander haben. Finde die Besonderheit heraus, um mehr über das Koordinatensystem zu lernen.

• Senkrechte Gerade ... Eine Gerade steht senkrecht auf die Rechtsachse. Was kann man über alle Punkte sagen, die auf dieser Geraden liegen?

• Waagrechte Gerade ... Eine Gerade ist parallel zur Rechtsachse. Welche Gemeinsamkeit haben alle Punkte, die auf dieser Geraden liegen?

• Ursprungsgerade ... Eine Gerade ist schräg und geht durch den Ursprung (0,0). Welche Gemeinsamkeit haben alle Punkte, die auf dieser Geraden liegen?

• Schräge Gerade ... Eine Gerade ist schräg und kann beliebig beliebig hoch liegen. Welche Gemeinsamkeit haben alle Punkte, die auf dieser Geraden liegen?

• Freie_Lage ... Eine Gerade, die du beliebig platzieren kannst. Welche Gemeinsamkeit haben alle Punkte, die auf dieser Geraden liegen? Experimentiere herum.

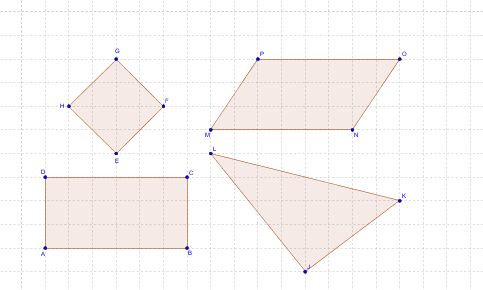
• Rechteck ... Und wie sieht es bei den Eckpunkten von Rechtecken aus?

• Parallelogramme ... Bei Pallelogrammen wird es sicher noch schwieriger, etwas zu entdecken!

• Haus zeichnen ... von einem Haus sind einige Punkte und deren Koordinaten gegeben. Ergänze die fehlenden Punkte, indem du sie per Tastatur eingibst. Dabei musst du einige fehlenden Koordinaten ergänzen. Das, was du in den letzten Untersuchungen gelernt hast, wird dir hier helfen.

Bei dieser Aufgabe gibt es keine einfache Lösung. Du hast etwas erforscht, vielleicht auch entdeckt und deine Erfahrungen niedergeschrieben. Lass deine Texte von deinem Mathelehrer oder einem Mitschüler anschauen, was sie davon halten.

Autoren: Reinhard Schmidt, Birgit Lachner, Wilfried Dutkowski