Rechteck - Flächeninhalt und Eigenschaften: Unterschied zwischen den Versionen
Main>Karl Kirst (Kategorie:Mathematik 5) |
Main>Karl Kirst (Kurzinfo Quiz) |
||
| Zeile 1: | Zeile 1: | ||
{{Diese Seite|ist einer von mehreren [[Flächeninhalt#Lernpfade|Lernpfaden zum Thema Flächeninhalt]].}} | {{Diese Seite|ist einer von mehreren [[Flächeninhalt#Lernpfade|Lernpfaden zum Thema Flächeninhalt]].}} | ||
{| | {| | ||
|{{Lernpfad-M|[[Bild:Rechteck1.jpg|200px|left]]{{Kurzinfo- | |{{Lernpfad-M|[[Bild:Rechteck1.jpg|200px|left]]{{Kurzinfo-2|M-digital|Quiz}} | ||
In dieser Unterrichtseinheit finden sich Fragen und Aufgaben rund ums Rechteck. Die Formel für den Flächeninhalt wird selbständig erarbeitet und auch eingeübt. Ergebnisse werden im Heft festgehalten. Möglichkeiten zur Differenzierung sind vorgesehen. | In dieser Unterrichtseinheit finden sich Fragen und Aufgaben rund ums Rechteck. Die Formel für den Flächeninhalt wird selbständig erarbeitet und auch eingeübt. Ergebnisse werden im Heft festgehalten. Möglichkeiten zur Differenzierung sind vorgesehen. | ||
<br>'''Voraussetzungen: '''Umfang und die wichtigsten Eigenschaften eines Rechtecks, erste Überlegungen zur Flächenmessung | <br>'''Voraussetzungen: '''Umfang und die wichtigsten Eigenschaften eines Rechtecks, erste Überlegungen zur Flächenmessung | ||
Version vom 5. März 2011, 22:24 Uhr
| Vorlage:Lernpfad-M |
Geometrische Figuren
In der Geometrie gibt es verschiedene geometrische Figuren.
Welche kennst du bereits?
Klicke auf folgenden Link und versuche, die Namen der Figuren zu nennen. Wenn du eine Figur nicht kennst, fahre mit der Maus auf die Figur und lass dir anzeigen, wie sie heißt. Versuche, dir den Namen zu merken!
Vorsicht: Eine der Figuren heißt "Deltoid". Dieser Begriff wird in Österreich verwendet. Welchen Namen kennst du für diese Figur?
Flächenmessung (Wiederholung)
- 1. Informiere dich in folgendem Hefteintrag/Seite 1 wie man Flächen messen kann.
- 2. Was ist 1 cm² (1 Quadratzentimeter)?
- 3. Veranschauliche deine Überlegungen an Hand einer Zeichnung im Heft.
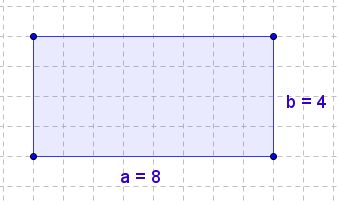
Flächeninhalt eines Rechtecks
|
Weitere Eigenschaften
Welche weiteren Eigenschaften eines Rechtecks kennst du? Mach dir Gedanken zu folgenden Fragen und notiere deine Ergebnisse:
- Wie berechnet man den Umfang eines Rechtecks?
- Wie groß sind die Winkel eines Rechtecks?
- Wie viele Symmetrieachsen hat ein Rechteck?
Übertrage die Sätze in dein Heft und vervollständige sie:
Merke: Eigenschaften des Rechtecks
- Je zwei gegenüberliegende Seiten sind ..............................................................
- Die zwei Diagonalen eines Rechtecks sind .........................................................
Kontrolle der bisherigen Ergebnisse
Vergleiche deine bisherigen Ergebnisse und Vermutungen aus Aufgabe 3 und 4 mit den folgenden Möglichkeiten:
Übungen online!
Hier findest zahlreiche Aufgaben zu Flächeninhalt und Umfang. Gleichzeitig kannst du deine Berechnungen veranschaulichen, indem du mit der Maus den Eckpunkt C verschiebst. Schaffst du es die 195-Punkte-Marke zu überspringen?
Teste dich!
Forschungsauftrag
Hier siehst du das Fußballfeld der Allianz Arena in München.
- Schätze die Größe des Feldes.
- Suche dir nun die entsprechenden Maße im Internet und berechne die Fläche des Fußballfeldes genau.
- Die Größe eines Rasenstücke vom Typ "Powerrasen" beträgt: 2,20 m x 15 m. Wie viele Rasenstücke wurden verlegt?
- Das Gewicht eines Rasenstücks beträgt 1,2 t. Wie viele Tonnen Rasen mussten angefahren werden um die gesamte Rasenfläche zu belegen?
<popup name="Lösung"> 1. ungefähr 8000 m2
2. netto (Fußballfeld): 68 m x 105 m = 7140 m2; brutto (gesamte Rasenfläche): 72 m x 111 m = 7992 m2
3. 243
4. 291,6 t </popup>
Zusammenhang Umfang - Flächeninhalt
In einer Streichholzschachtel befinden sich noch 12 Streichhölzer. Jedes einzelne Streichholz ist 5 cm lang.
- Wie viele "Rechtecke" kannst du aus den Streichhölzern legen, wenn du alle verwendest?
- Alle "Rechtecke" haben denselben Umfang. Wie lang ist dieser?
- Bestimme die Flächeninhalte deiner Rechtecke. Welches hat den größten Flächeninhalt?
Quelle: LS5, S.178 <popup name="Lösung"> 1. 3 verschiedene Rechtecke
2. 60 cm
3. 125 cm2, 200cm2, 225cm2 </popup>
Drei Spiele zum Schluss!!
- Es gibt verschiedene Möglichkeiten aus 5 Pentominos ein Quadrat zusammenzusetzen. Finde mindestens eine. Welchen Flächeninhalt hat das "Pentominoquadrat"? <popup name="Lösung">Flächeninhalt: 25 FE; eine mögliche Lösung:
 </popup>
</popup> - Mit diesem Memo-Spiel wiederholst du noch einmal die verschiedenen geometrischen Figuren.
- Hier kannst du Flächen messen und schätzen.
Kleine Testfragen
- ↑ BMT 2006