Lineare Funktionen/Station 3

Lineare Funktionen

• Station 1: Proportionalität
• Übung 1
• Station 2: Steigung
• Übung 2
• Station 3: Beschreibung allgemeiner Geraden
• Übung 3
• Station 4: Aufstellen eines Funktionterms
• Übung 4
• Abschluss

Mathematik-digital.de

Station 3: Beschreibung allgemeiner Geraden

In Station 2 hast du gelernt, wie man die Steigung von Geraden im Koordinatensystem bestimmen kann. Allerdings haben wir bislang immer nur solche Geraden betrachtet, die Graph einer proportionalen Funktion waren, also Geraden, die durch den Ursprung verlaufen. In dieser Station lernst du, wie man beliebige Geraden durch eine Funktionsgleichung beschreiben kann, also auch solche, die keine Ursprungsgeraden sind.

Sind solche Geraden überhaupt relevant?

Starte die App und überlege genau, bevor du die Fragen beantwortest.

Ursprungsgeraden reichen nicht!

Ziehe die Begriffe unten in die richtige Lücke.

Bis jetzt haben wir immer nur Funktionen proportionaler Zusammenhänge der Form $f(x)=m\cdot x$ betrachtet. Die Graphen zu diesen Funktionen waren immer Geraden, die durch den Ursprung verlaufen.
Wie du eben gesehen hast, gibt jedoch Situationen, die mit solchen Funktionen und Geraden nicht mehr beschrieben werden können.
Dies ist vor allem dann der Fall, wenn beim x-Wert 0 der zugehörige y-Wert nicht gleich 0 ist. In unserem Fall bedeutete das, dass zum Zeitpunkt t=0 die zugehörige Wassermenge nicht 0m³, sondern zum Beispiel 400m³ war.
Trotzdem stellt der Graph noch eine Gerade dar, da die Wassermenge immer noch gleichmäßig zu- oder abnimmt.Diese ist jedoch im Vergleich zur Ursprungsgeraden nach oben oder unten verschoben.

Wie aber sieht eine Funktionsgleichung aus, die eine "allgemeine" Gerade richtig beschreiben kann?

Lineare Funktion - Funktionsterm

Wir wissen bereits, wie der Funktionsterm von Funktionen aussieht, deren Graphe eine Ursprungsgerade ist: $f(x) =m\cdot x.$

Jetzt stellt sich aber die Frage, wie denn dann ein Funktionsterm aussehen muss, der jeder beliebige Gerade beschreiben kann? Um dies herauszufinden, folge bitte den Anleitungen in der nächsten App. Viel Erfolg!

Ergebnis:
Jede beliebige Gerade im Koordinatensystem kann durch die Funktionsgleichung $f(x)=m\cdot x+t$ beschrieben werden.

Alle diese Funktionen, deren Graph eine Gerade ist und deren Funktionsgleichung die Form $\color{blue} f(x)=m\cdot x+t$ heißen lineare Funktionen.

Merke

Jede Funktion, die durch die Funktiongleichung $\color{blue}f(x)=m\cdot x+t$ beschrieben wird, heißt lineare Funktion.
Der Graph einer linearen Funktion ist immer (irgend) eine Gerade.

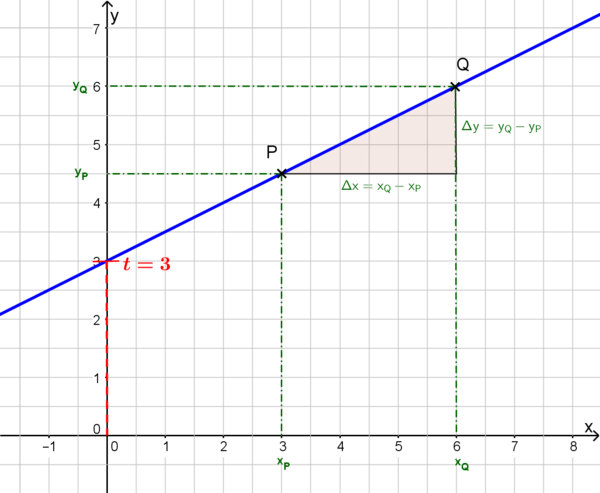
• Man nennt t den y-Achsenabschnitt der Geraden.
• m bezeichnet die Steigung der Geraden.
  
  
• Verläuft der Graph durch die Punkte P(x_P|y_P) und Q(x_Q|y_Q), so gilt für die Geradensteigung: $m=\frac{y_Q-y_P}{x_Q-y_Q}$.
  

Beispiel
Bei obiger Gerade gilt:

• y-Achsenabschnitt: $\color{red}t=3$
• Steigung: $\color{OliveGreen}m=\frac{6-4,5}{6-3}=\frac{1,5}{3}=0,5$

Damit lautet die Funktionsgleichung: $\color{blue}f(x)=0,5x+3$

Übungen zum Verständnis

Übung 10: Ordne zu! Starte die App und entscheide, welche der dargestellten Graphen zu einer linearen Funktion gehören! (leicht)

Aufgabe 6

{{{2}}}

Übung 11: Finde die Funktionsgleichung! Starte die App und entscheide, welcher Funktionsterm den dargestellten Graphen richtig beschreibt. (nicht ganz ohne)

--- aktuelle Meldung: Entwarnung im Bergwerk ---

Das Bergwerk hat ein Gesamtvolumen von 1800m3 und steht bereits völlig unter Wasser, als es endlich gelingt, neue Pumpen in Betrieb zu nehmen. Die neuen Pumpen haben eine max. Pumpleistung von 150m³ Wasser pro Stunde. Wie lange wird es dauern, bis das Bergwerk wieder frei von Grundwasser ist?

Entscheide für dich selbst, in welchem Schwierigkeitsniveau du die Aufgabe bearbeiten möchtest!

1. Version der Aufgabe - mittlerere Schwierigkeitsgrad	2. Version der Aufgabe - hoher Schwierigkeitsgrad
[A7 - mittlere Schwierigkeit anzeigen][Verstecken] Aufgabe 7	[A7 - hohe Schwierigkeit anzeigen][Verstecken] Aufgabe 7

---

Nimm dir bitte kurz Zeit, und gib eine Rückmeldung zu dieser Station.

---

Alle Aufgaben erledigt? Dann kann's weitergehen!

Datei:Binoculars-1015267 1920.jpg

Hier geht es weiter zur letzten Übung......

Lineare Funktionen

• Station 1: Proportionalität
• Übung 1
• Station 2: Steigung
• Übung 2
• Station 3: Beschreibung allgemeiner Geraden
• Übung 3
• Station 4: Aufstellen eines Funktionterms
• Übung 4
• Abschluss

Mathematik-digital.de