Sinus- und Kosinusfunktion/2.2 Kosinusfunktion: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Florian Ferstl
(Die Seite wurde neu angelegt: „{{Lernpfad Sinus und Kosinusfunktion}} <div style=" width: 80%; border: 2px solid #c6d745; background-color:#c6d745; padding:7px;font-size:1px; height:1px; …“)
 
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(19 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Lernpfad Sinus und Kosinusfunktion}}
{{Navigation verstecken|{{Lernpfad Sinus- und Kosinusfunktion}}
|Lernschritte einblenden|Lernschritte ausblenden}}


==Station 2: Sinusfunktion und Kosinusfunktion==


<div style="  width: 80%; border: 2px solid #c6d745; background-color:#c6d745; padding:7px;font-size:1px; height:1px; border-bottom:1px solid #c6d745;"></div>
===2.2 Kosinusfunktion===
<div style="  width: 80%; border: 2px solid #c6d745; background-color:#ffffff; align:center; padding:7px;">


==Station 2: Sinusfunktion und Kosinusfunktion==
{{Box|1=Üben|2=
<br>
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie).
{|
Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein.
Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.


===2. Kosinusfunktion===
<ggb_applet id="AtX3XWby" width="100%" height="450" border="888888" />
'''Auftrag 1:'''
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). <br>
Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein.
<br>Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.


<iframe scrolling="no" title="Kosinusfunktion am Einheitskreis" src="https://www.geogebra.org/material/iframe/id/AtX3XWby/width/1648/height/670/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="1148px" height="365px" style="border:0px;"> </iframe>
|3=Üben}}


Halte deine Erkenntnisse nun schriftlich fest:


'''Auftrag 2:'''
{{Box|Aufgabe - 2.2 Kosinusfunktion|Bearbeite den zugehörigen Auftrag auf dem [[Media:AB zum Lernpfad Sinus-und Kosinusfunktion.docx|Arbeitsblatt]].|Arbeitsmethode}}
Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.


<br>
<br>


'''Auftrag 3:'''
{{Box
Überlege: Was könnte das bedeuten?
|Titel= Frage
<math> cos(-\frac{\pi}{2})  </math>    oder  <math> cos(410^\circ) </math>
|Inhalt= Überlege: Was könnte das bedeuten?
<math> cos(-\frac{\pi}{2})  </math>    oder  <math> cos(410^\circ) </math>
Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft.
|Klasse= Frage
}}
 
{{Lösung versteckt|1=Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn.
[[Datei:Negativer Winkel.png|center|200px|Negativer Winkel]]
|2=Lösung 'Negativer Winkel' anzeigen|3=Lösung verbergen}}
 


Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft.  
{{Lösung versteckt|1=
<br>
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder <math>3\pi</math>
{|
[[Datei:Winkel größer 360°.png|center|200px|Winkel größer 360°]]
|2=Lösung 'Großer Winkel' anzeigen|3=Lösung verbergen}}


|<popup name = "Lösung negativer Winkel">
Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn.
[[Datei:Negativer Winkel.png|links|x200px|Negativer Winkel]]<br><br><br><br><br><br><br><br><br><br><br>ok?
</popup>


Teste, ob du alles verstanden hast!


|<popup name = "Lösung große Winkel">
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder <math>3\pi</math>
[[Datei:Winkel größer 360°.png|links|x200px|Winkel größer 360°]]<br><br><br><br><br><br><br><br><br><br><br>ok?
</popup>
|}


<br>
{{Box|1=Üben|2='''Kosinusfunktion verstanden?'''  
<br>
'''Auftrag 4:'''<br>
Quiz: Verstehst du die Kosinusfunktion?


<iframe src="https://learningapps.org/watch?v=p12tazmca17" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
{{LearningApp|app=p12tazmca17|width=100%|height=400px}}


----
|3=Üben}}
'''Erste Wiederholung ist geschafft. War nicht so schwer. Weiter gehts! :)
{|border="0" cellspacing="0" cellpadding="4"
|align = "left" width="60"|[[Datei:Pfeil weiter.png|50px]]
|align = "left"|[[/3. Allgemeine Sinusfunktion|'''Hier geht es weiter''']]'''...'''
|}


'''So, nun hast du alles wiederholt, was wir schon besprochen haben. Jetzt kommt was neues. Du darfst gespannt sein! :)


{{Fortsetzung|weiter=Allgemeine Sinusfunktion|weiterlink=../3. Allgemeine Sinusfunktion}}






{{Lernpfad Sinus und Kosinusfunktion}}
[[Kategorie:Interaktive Übung]]
[[Kategorie:GeoGebra]]
[[Kategorie:LearningApps]]

Aktuelle Version vom 6. Dezember 2024, 22:20 Uhr

Sinus- und Kosinusfunktion
  1. Bogenmaß
    Beispiel Sinus.png
  2. Sinusfunktion
  3. Kosinusfunktion
  4. Allgemeine Sinusfunktion
  5. Allgemeine Sinusfunktion - Parameter
  6. Übung 1
  7. Übung 2
  8. Abschluss
  9. Tangensfunktion
Mathematik-digital.de

Station 2: Sinusfunktion und Kosinusfunktion

2.2 Kosinusfunktion

Üben

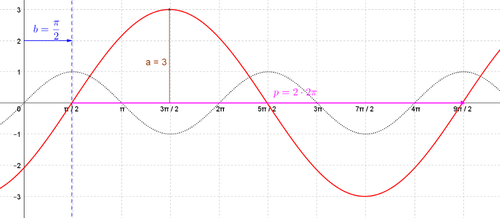
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.

GeoGebra

Halte deine Erkenntnisse nun schriftlich fest:

Aufgabe - 2.2 Kosinusfunktion
Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.


Frage

Überlege: Was könnte das bedeuten? oder

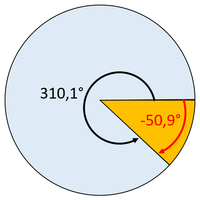
Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft.

Ein negativer Winkel bedeutet, dass man den Winkel nicht im Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn.

Negativer Winkel


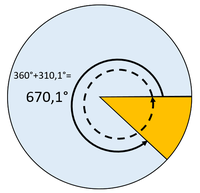
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder

Winkel größer 360°


Teste, ob du alles verstanden hast!


Üben

Kosinusfunktion verstanden?


So, nun hast du alles wiederholt, was wir schon besprochen haben. Jetzt kommt was neues. Du darfst gespannt sein! :)

Allgemeine Sinusfunktion
Abgerufen von „https://unterrichten.zum.de/index.php?title=Sinus-_und_Kosinusfunktion/2.2_Kosinusfunktion&oldid=139057“