Lernpfad 8a - Volumina und Flächen/Kreisfläche: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Box|Info|Auf dieser Seite erkundest du den Flächeninhalt eines Kreises und findest heraus, wie man diesen berechnen kann.|Kurzinfo
{{Box|Info|Auf dieser Seite erkundest du den Flächeninhalt eines Kreises und findest heraus, wie man diesen berechnen kann. Notiere alle unter der Überschrift ''1.2 Flächeninhalt eines Kreises'' in deinem Heft.|Kurzinfo
}}
}}


==Erste Erkundung==
==<span class="brainy hdg-magnifying-glass fa-1,5x"></span> Erste Erkundungen==
Mika und Jasmin gehen mit ihrer Familie in der Pizzeria ''Bella Italia'' essen. Beide entscheiden sich für eine normal große Pizza Margherita. Die Kellnerin schlägt vor: "Nehmt doch eine große Pizza und teilt sie euch".
Mika und Jasmin gehen mit ihrer Familie in der Pizzeria ''Bella Italia'' essen. Beide entscheiden sich für eine mittlere  Pizza Margherita. Die Kellnerin schlägt vor: "Nehmt doch eine große Pizza und teilt sie euch".


[[Datei:Preisvergleich_Pizza.png|500x500px]]{{Box|Erkundung|Ist der Vorschlag der Kellnerin sinnvoll? Suche gemeinsam mit deinem Partner nach Möglichkeiten, zwei normale Pizzen und eine große Pizza zu vergleichen.|Unterrichtsidee
[[Datei:Preisvergleich_Pizza.png|500x500px]]{{Box|Erkundung|Ist der Vorschlag der Kellnerin sinnvoll? Suche gemeinsam mit deinem Partner nach Möglichkeiten, zwei mittlere Pizzen und eine große Pizza zu vergleichen.|Unterrichtsidee
}}{{Lösung versteckt|Überlege dir verschiedene Strategien, den Flächeninhalt eines Kreises zu berechnen. Für die Berechnung des Flächeninhaltes eines Trapezes haben wir Zerlegungs- und Ergänzungsstrategien genutzt.|Tipp  anzeigen|Tipp verbergen}}
}}{{Lösung versteckt|Überlege dir verschiedene Strategien, den Flächeninhalt eines Kreises zu berechnen. Für die Berechnung des Flächeninhaltes eines Trapezes haben wir Zerlegungs- und Ergänzungsstrategien genutzt.|Tipp  anzeigen|Tipp verbergen}}


==Die Kreisfläche bestimmen==
==<span class="brainy hdg-binoculars fa-2x"></span>Die Kreisfläche bestimmen==
Mika und Jasmin entscheiden sich dazu, die große Pizza zu teilen. Beim Aufteilen der Pizza auf zwei Teller legen sie mit den einzelnen Pizzastücken verschiedene Muster.
Mika und Jasmin entscheiden sich dazu, die große Pizza zu teilen. Beim Aufteilen der Pizza auf zwei Teller legen sie mit den einzelnen Pizzastücken verschiedene Muster.


[[Datei:Kreisfläche_Pizzastuecke.png|400x400px]]{{Box|Aufgabe 1|Erkläre, warum die Flächeninhalte beider Figuren gleich sind.  
 
[[Datei:Kreisfläche_Pizzastuecke.png|400x400px]]
 
<br />{{Box|Aufgabe 1|Erkläre, warum die Flächeninhalte beider Figuren gleich sind.  


Erkläre, wie die neue Anordnung der Pizzastücke zur Berechnung der Kreisfläche genutzt werden kann.
Erkläre, wie die neue Anordnung der Pizzastücke zur Berechnung der Kreisfläche genutzt werden kann.
Zeile 19: Zeile 22:
}}Sollte das Applet nicht richtig laden, klicke [https://www.geogebra.org/m/rnp6jA8y].<ggb_applet id="rnp6jA8y" width="750" height="400" />{{Lösung versteckt|Bei der Erklärung hilft dir der Kreisumfang.|Tipp 1 anzeigen|Tipp verbergen}}{{Lösung versteckt|Die Form der aufgeteilten Pizza ist ein Parallelogramm oder - bei ganz feiner Zerlegung - ein Rechteck. Wie berechnest du den Flächeninhalt dieser Figuren?|Tipp 2 anzeigen|Tipp verbergen}}{{Lösung versteckt|Erkläre, warum man den Flächeninhalt eines Kreises mit dem Term <math> r \cdot r \cdot \pi</math> berechnen kann.|Tipp 3 anzeigen|Tipp verbergen}}
}}Sollte das Applet nicht richtig laden, klicke [https://www.geogebra.org/m/rnp6jA8y].<ggb_applet id="rnp6jA8y" width="750" height="400" />{{Lösung versteckt|Bei der Erklärung hilft dir der Kreisumfang.|Tipp 1 anzeigen|Tipp verbergen}}{{Lösung versteckt|Die Form der aufgeteilten Pizza ist ein Parallelogramm oder - bei ganz feiner Zerlegung - ein Rechteck. Wie berechnest du den Flächeninhalt dieser Figuren?|Tipp 2 anzeigen|Tipp verbergen}}{{Lösung versteckt|Erkläre, warum man den Flächeninhalt eines Kreises mit dem Term <math> r \cdot r \cdot \pi</math> berechnen kann.|Tipp 3 anzeigen|Tipp verbergen}}


==Die Kreisfläche==
 
{{Box|Merke|Wenn man sich einen Kreis in viele Stücke zerlegt denkt, kann man seinen Flächeninhalt aus Radius und Umfang berechnen. Für die Berechnung der Kreisfläche gilt dann:
 
<blockquote><math>A= r^2 \cdot \pi  </math>.</blockquote>
[[../Hefteintrag Umfang Kreis|<span class="fa fa-arrow-circle-left "></span> zurück]]{{Fortsetzung|weiter=zum Hefteintrag|weiterlink=Lernpfad 8a - Volumina und Flächen/Merksatz Fläche}}
[[Datei:Kreisfläche Visualisierung.png|450px]]
Übernehme auch die Skizze in dein Heft und ergänze deinen Hefteintrag um ein Beispiel.|Merksatz
}}{{Box|Aufgabe 2|Berechne die Kreisfläche. Runde auf zwei Nachkommastellen.  
# Der Radius des Kreises beträgt <math>r=3</math>cm.
# Der Radius des Kreises beträgt <math>r=5</math>mm.
# Der Radius des Kreises beträgt <math>d=12</math>cm.
# Der Radius des Kreises beträgt <math>d=8</math>m.|Übung
}}{{Lösung versteckt|Lösungen:
# <math>A=(3cm)^2 \cdot \pi \approx 28,27cm^2</math>
# <math>A= (5mm)^2 \cdot \pi \approx 78,54mm^2</math>
# <math>A= (\frac{12cm}{2})^2 \cdot \pi \approx 113,1cm^2</math>
# <math>A= (\frac{8m}{2})^2 \cdot \pi \approx 50,27cm</math>|Lösung anzeigen|Lösung verbergen}}{{Box|Aufgabe 3|Vergleiche die Pizzaangebote von ''Bella Italia''. Bei welchem Angebot bekommt man am meisten Pizza für den günstigsten Preis?|Übung
}}{{Lösung versteckt|Was kostet bei den drei Größen jeweils 1 cm<sup>2</sup> Pizza?|Tipp anzeigen|Tipp verbergen}}{{Lösung versteckt|* kleine Pizza: <math>A=(9cm)^2 \cdot \pi \approx 254,47cm^2</math>, das sind bei einem Preis von 8,50€ etwa 3,3ct pro 1 cm<sup>2</sup> Pizza
* mittlere Pizza: <math>A=(12cm)^2 \cdot \pi \approx 452,39cm^2</math>, das sind bei einem Preis von 14€ etwa 3,1ct pro 1 cm<sup>2</sup> Pizza
* große Pizza: <math>A=(18cm)^2 \cdot \pi \approx 1017,87cm^2</math>, das sind bei einem Preis von 26,50€ etwa 2,6ct pro 1 cm<sup>2</sup> Pizza
Die große Pizza ist das günstigste Angebot. Die kleine Pizza ist im Vergleich etwas teurer als die mittlere Pizza.|Lösung anzeigen|Lösung verbergen}}{{Fortsetzung|weiter=Hier geht es zu Übungen rund um den Kreis|weiterlink=Lernpfad 8a - Volumina und Flächen/Übung}}

Aktuelle Version vom 28. Juni 2023, 03:59 Uhr

Info
Auf dieser Seite erkundest du den Flächeninhalt eines Kreises und findest heraus, wie man diesen berechnen kann. Notiere alle unter der Überschrift 1.2 Flächeninhalt eines Kreises in deinem Heft.

Erste Erkundungen

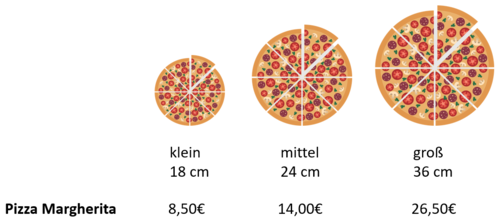
Mika und Jasmin gehen mit ihrer Familie in der Pizzeria Bella Italia essen. Beide entscheiden sich für eine mittlere Pizza Margherita. Die Kellnerin schlägt vor: "Nehmt doch eine große Pizza und teilt sie euch".

Preisvergleich Pizza.png

Erkundung
Ist der Vorschlag der Kellnerin sinnvoll? Suche gemeinsam mit deinem Partner nach Möglichkeiten, zwei mittlere Pizzen und eine große Pizza zu vergleichen.
Überlege dir verschiedene Strategien, den Flächeninhalt eines Kreises zu berechnen. Für die Berechnung des Flächeninhaltes eines Trapezes haben wir Zerlegungs- und Ergänzungsstrategien genutzt.

Die Kreisfläche bestimmen

Mika und Jasmin entscheiden sich dazu, die große Pizza zu teilen. Beim Aufteilen der Pizza auf zwei Teller legen sie mit den einzelnen Pizzastücken verschiedene Muster.


Kreisfläche Pizzastuecke.png


Aufgabe 1

Erkläre, warum die Flächeninhalte beider Figuren gleich sind.

Erkläre, wie die neue Anordnung der Pizzastücke zur Berechnung der Kreisfläche genutzt werden kann. Schaue dir hierfür auch weitere Beispiele für Zerlegungen des Kreises in dem folgenden Applet an.

Stelle einen Term zur Berechnung der Kreisfläche auf.

Sollte das Applet nicht richtig laden, klicke [1].

GeoGebra
Bei der Erklärung hilft dir der Kreisumfang.
Die Form der aufgeteilten Pizza ist ein Parallelogramm oder - bei ganz feiner Zerlegung - ein Rechteck. Wie berechnest du den Flächeninhalt dieser Figuren?
Erkläre, warum man den Flächeninhalt eines Kreises mit dem Term berechnen kann.


zurück

zum Hefteintrag
Abgerufen von „https://unterrichten.zum.de/index.php?title=Lernpfad_8a_-_Volumina_und_Flächen/Kreisfläche&oldid=135171“