Lernpfad 8a - Volumina und Flächen/Kreisumfang: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 27: | Zeile 27: | ||
{{Lösung versteckt| | {{Lösung versteckt|==Der Kreisumfang== | ||
==Der Kreisumfang== | |||
{{Box|Merke|Der Umfang U eines Kreises ist ungefähr dreimal so groß wie sein Durchmesser d. Genauer beschreibt die Kreiszahl <math>\pi\approx 3,14</math> das Verhältnis zwischen dem Umfang und dem Durchmesser: Für einen Kreis mit dem Radius <math>r</math> und dem Durchmesser <math>d=2r </math> gilt | {{Box|Merke|Der Umfang U eines Kreises ist ungefähr dreimal so groß wie sein Durchmesser d. Genauer beschreibt die Kreiszahl <math>\pi\approx 3,14</math> das Verhältnis zwischen dem Umfang und dem Durchmesser: Für einen Kreis mit dem Radius <math>r</math> und dem Durchmesser <math>d=2r </math> gilt | ||
<blockquote><math>U= d \cdot \pi = 2 \cdot r \cdot \pi </math>.</blockquote> | <blockquote><math>U= d \cdot \pi = 2 \cdot r \cdot \pi </math>.</blockquote> | ||
| Zeile 61: | Zeile 60: | ||
|Muster erkannt & mit Frau Krause besprochen |Muster erkannt & mit Frau Krause besprochen}} | |Muster erkannt & mit Frau Krause besprochen |Muster erkannt & mit Frau Krause besprochen}} | ||
Version vom 23. Juni 2023, 09:10 Uhr
Forscherauftrag
Kreise begegnen uns vielfach im Alltag. Suche dir mindestens fünf kreisrunde Gegenstände im Klassenzimmer. Bestimme den Durchmesser und den Umfang dieser Gegenstände, indem du geeignete Messinstrumente verwendest (z.B. Lineal, Faden, Maßband).
Halte deine Ergebnisse in einer Tabelle in deinem Heft unter der Überschrift fest.
| Gegenstand | Durchmesser d (in cm) | Umfang U (in cm) |
|---|---|---|
| ... | ... | ... |
Betrachte die Messergebnisse in der Tabelle. Kannst du eine Regelmäßigkeit erkennen?
Untersuche, welcher Zusammenhang zwischen dem Durchmesser d und dem Umfang U des Kreises besteht. Notiere deine Vermutungen.Pia hat folgende Messergebnisse. Sie schaut sich das Verhältnis von Umfang und Durchmesser an und ergänzt ihre Tabelle.
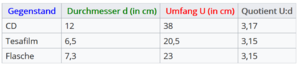
Vergleicht eure Ergebnisse mit anderen Zweierteams und besprecht sie anschließend mit Frau Krause.
Übungen
Berechne den Kreisumfang. Runde auf zwei Nachkommastellen.
- Der Radius des Kreises beträgt cm.
- Der Radius des Kreises beträgt mm.
- Der Radius des Kreises beträgt cm.
- Der Radius des Kreises beträgt m.
Lösungen:
Bestimme die Länge der Strecke, die ein Fahrrad mit einem 26-Zoll-Reifen bei einer Radumdrehung zurück legt.
Hinweis: 1 Zoll entspricht 2,54cmDer Raddurchmesser beträgt 26 Zoll und damit 66,04 cm. Es gilt .
Mit einer Umdrehung legt das Fahrrad 207,47 cm zurück.




