Benutzer:Alexweller/Lineares und exponentielles Wachstum: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Benutzer:Alexweller/Lineares und exponentielles Wachstum
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 17: | Zeile 17: | ||
{{Box|Lineares Wachstum|Wenn die Wertepaaare konstant um den gleichen Wert wachsen, liegt ein lineares Wachstum vor. | {{Box|Lineares Wachstum|Wenn die Wertepaaare konstant um den gleichen Wert wachsen, liegt ein lineares Wachstum vor. | ||
f(x)= mx +b |Hervorhebung1}} | <math>f(x)= mx +b </math>|Hervorhebung1}} | ||
{{Autorenbox}} | {{Autorenbox}} | ||
Aktuelle Version vom 22. April 2023, 18:19 Uhr
Lernpfad
Mathematisches Wachstum bezeichnet die Zunahme einer bestimmten Messgröße im Zeitverlauf. Das Gegenteil von Wachstum ist die Schrumpfung, also die Abnahme einer Messgröße – teilweise auch als Zerfall bezeichnet.
wikipedia
Auf dieser Seite werden verschiedene Wachstumsvorgänge anhand unterschiedlicher Beispiele erfahrbar gemacht und untersucht.Lernpfadwerkzeuge (nur sichtbar für angemeldete Benutzer)
Hier wächst etwas
Wenn man morgens in eine Bäckerei kommt und ein Brot kaufen möchte, dann hat dieses eine bestimmten Preis. Kauft man zwei Brote, so muss man den Preis von zwei Broten bezahlen. Ein drittes Brot kostet dreimal so viel wie das erste Brot, welches gekauft wurde.
Bei jedem weiteren Brot würde man den Preis eines einzelnen Brotes zum Gesamtpreis hinzuzählen, addieren. In einer Wertetabelle ausgedrückt, kann man diese durch Additionspfeile zum nächsten Wertepaar darstellen.
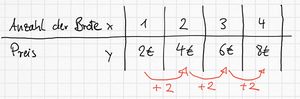Eine dynamische Darstellung siehst Du unter folgendem Link:
https://www.geogebra.org/m/wappbt8j
Lineares Wachstum
Wenn die Wertepaaare konstant um den gleichen Wert wachsen, liegt ein lineares Wachstum vor.
