Sinus- und Kosinusfunktion: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Karl Kirst (Kurzinfo M-digital) |
Keine Bearbeitungszusammenfassung |
||
| (31 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad | {{Lernpfad| | ||
===In diesem Lernpfad=== | |||
*wiederholst du das Bogenmaß | |||
In diesem Lernpfad | *wiederholst du, wie man vom Einheitskreis zur Sinusfunktion und zur Kosinusfunktion kommt | ||
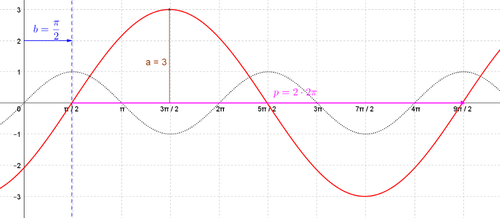
*lernst du, was man unter der "allgemeinen Sinusfunktion" bzw. der "allgemeinen Kosinusfunktion" versteht | |||
* | *lernst du welchen Einfluss die Parameter der allgemeinen Funktion auf den Verlauf des Graphen haben | ||
* | *lernst du wie die Tangensfunktion aussieht | ||
* | ===Das solltest du bereits können=== | ||
* | |||
* | |||
Das solltest du bereits können | |||
*Bogenmaß | *Bogenmaß | ||
*Sinus und Kosinus am Einheitskreis | *Sinus und Kosinus am Einheitskreis | ||
[[Datei:Logo Mathematik-digital 2011.png|200px|right|verweis=Mathematik-digital|Mathematik-digital]] | |||
}} | }} | ||
{{Lernpfad Sinus- und Kosinusfunktion}} | |||
=== Erklärung der verwendeten Symbole=== | ===Erklärung der verwendeten Symbole=== | ||
Damit du den Lernpfad ohne Probleme durchführen kannst ist es wichtig, <br> | Damit du den Lernpfad ohne Probleme durchführen kannst ist es wichtig, <br> | ||
dass du die verwendeten Symbole und Grafiken kennst und weißt, was sie für dich bedeuten. | dass du die verwendeten Symbole und Grafiken kennst und weißt, was sie für dich bedeuten. | ||
{{Box|Merke|Hierbei handelt es sich um einen Merksatz. '''Merksätze''' musst du grundsätzlich '''immer in dein Schulheft übertragen''', inklusive einer farbigen Umrahmung.|Merksatz}} | |||
{{Box|Aufgabe|Immer wenn du diesen Kasten mit dem Stiftsymbol siehst, gibt es eine '''Aufgabe schriftlich im Schulheft zu bearbeiten!'''|Arbeitsmethode}} | |||
{{Box|Üben|Übungsaufgaben werden entweder '''online oder im Übungsheft''' bearbeitet. Genaueres steht jeweils mit dabei.|Üben}} | |||
{{ | {{Box-spezial | ||
|Titel= Frage | |||
|Inhalt= So werden Fragestellungen gekennzeichnet, über die du dir '''besonders Gedanken machen''' solltest. | |||
|Farbe= #cccccc | |||
|Icon= {{Icon question}} | |||
}} | |||
{{Box||In diesen Kästen werden meist Hinweise gegeben, wie eine App zu bedienen ist. '''Lies dir diese Anweisungen sorgfältig durch und befolge sie!'''|Hervorhebung1}} | |||
<div class="grid"> | |||
<div class="width-1-4">[[Datei:Time-1019921 1920.jpg|180px|Zeitwächter]]</div> | |||
< | <div class="width-3-4">Vergiss nicht, dass du die Zeit im Auge behältst. <br>Oberstes Ziel ist zwar, dass du alles verstehst, trotzdem solltest du nicht trödeln!</div> | ||
</div> | |||
<div class="grid"> | |||
< | <div class="width-1-4">[[Datei:Help-1013699 1920.jpg|180px|Teamwork]]</div> | ||
<div class="width-3-4"> | |||
Hast du '''Fragen oder Probleme''' zu einer Station oder verstehst du eine Aufgabe nicht? | |||
< | |||
Kein Problem, hinterlasse einfach eine Nachricht auf der Pinnwand. Ein Mitschüler kann dir dann helfen, wenn er selbst schon fertig ist. Klicke einfach auf [http://LearningApps.org/watch?v=p35pzujjc16 '''Hilfe-Station'''].</div> | |||
</div> | |||
<div class="grid"> | |||
<div class="width-1-4">[[Datei:Communication-1015376 1920.jpg|180px|Feedback]]</div> | |||
<div class="width-3-4">Hast du irgendwelche netten oder kritischen Anmerkungen zum Lernpfad? Hinterlasse einen Zettel an der | |||
[http://LearningApps.org/watch?v=pr21dzxh316 '''Pinnwand''']. Natürlich anonym!</div> | |||
</div> | </div> | ||
< | <div class="width-7-8"> '''Nun kann es aber endlich losgehen! Viel Erfolg! Beginne doch gleich mit der ersten Station!'''</div> | ||
{{Lernpfad | {{Fortsetzung|weiter=Weiter zum Lernpfad Bogenmaß|weiterlink=/1. Bogenmaß}} | ||
[[Kategorie: | {{Autoren|Florian Ferstl}} | ||
[[Kategorie: | [[Kategorie:Mathematik]] | ||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Trigonometrische Funktionen]] | |||
[[Kategorie:Analysis]] | |||
Version vom 24. April 2022, 10:40 Uhr
Lernpfad
In diesem Lernpfad
- wiederholst du das Bogenmaß
- wiederholst du, wie man vom Einheitskreis zur Sinusfunktion und zur Kosinusfunktion kommt
- lernst du, was man unter der "allgemeinen Sinusfunktion" bzw. der "allgemeinen Kosinusfunktion" versteht
- lernst du welchen Einfluss die Parameter der allgemeinen Funktion auf den Verlauf des Graphen haben
- lernst du wie die Tangensfunktion aussieht
Das solltest du bereits können
- Bogenmaß
- Sinus und Kosinus am Einheitskreis
Sinus- und Kosinusfunktion
- Bogenmaß
- Sinusfunktion
- Kosinusfunktion
- Allgemeine Sinusfunktion
- Allgemeine Sinusfunktion - Parameter
- Übung 1
- Übung 2
- Abschluss
- Tangensfunktion
Erklärung der verwendeten Symbole
Damit du den Lernpfad ohne Probleme durchführen kannst ist es wichtig,
dass du die verwendeten Symbole und Grafiken kennst und weißt, was sie für dich bedeuten.
Merke
Hierbei handelt es sich um einen Merksatz. Merksätze musst du grundsätzlich immer in dein Schulheft übertragen, inklusive einer farbigen Umrahmung.
Aufgabe
Immer wenn du diesen Kasten mit dem Stiftsymbol siehst, gibt es eine Aufgabe schriftlich im Schulheft zu bearbeiten!
Üben
Übungsaufgaben werden entweder online oder im Übungsheft bearbeitet. Genaueres steht jeweils mit dabei.
In diesen Kästen werden meist Hinweise gegeben, wie eine App zu bedienen ist. Lies dir diese Anweisungen sorgfältig durch und befolge sie!
Vergiss nicht, dass du die Zeit im Auge behältst.
Oberstes Ziel ist zwar, dass du alles verstehst, trotzdem solltest du nicht trödeln!
Oberstes Ziel ist zwar, dass du alles verstehst, trotzdem solltest du nicht trödeln!
Hast du Fragen oder Probleme zu einer Station oder verstehst du eine Aufgabe nicht?
Kein Problem, hinterlasse einfach eine Nachricht auf der Pinnwand. Ein Mitschüler kann dir dann helfen, wenn er selbst schon fertig ist. Klicke einfach auf Hilfe-Station.Hast du irgendwelche netten oder kritischen Anmerkungen zum Lernpfad? Hinterlasse einen Zettel an der
Pinnwand. Natürlich anonym!
Nun kann es aber endlich losgehen! Viel Erfolg! Beginne doch gleich mit der ersten Station!