Terme/Grundwissenübersicht - Alles auf einen Blick: Unterschied zwischen den Versionen

Aktuelle Version vom 23. April 2022, 16:07 Uhr

Diese Grundwissenseite dient als Übersicht über die wichtigsten Begriffe im Zusammenhang mit Termen.

Begriffe

Term: Ein Term ist ein Rechenausdruck, der einen Sachverhalt beschreibt und neben Zahlen auch Variablen enthalten kann.

Variable: Eine Variable ist ein Platzhalter (häufig Buchstaben), der durch verschiedene Einsetzungen ausgetauscht werden kann.

Definitionsmenge : Die Definitionsmenge ist die Menge der Zahlen, die bei der Einsetzung für eine Variable in einen Term zu einer sinnvollen Aussage führen.

Termwert: Der Termwert ist das Ergebnis, das man erhält, wenn man in den Term eine Zahl der Definitionsmenge einsetzt.

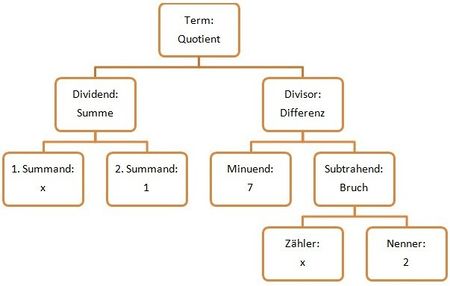
Termart: Die Termart wird durch das letzte ausgeführte Rechenzeichen festgelegt. (mehr Information)

Rechengesetze

Kommutativgesetz

$a + b = b + a$
$a \cdot b = b \cdot a$

für alle a, b, c

\in Q

Assoziativgesetz

$a + (b + c) = (a + b) + c = a + b + c$
$a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c$

für alle a, b, c

\in Q

Distributivgesetz

$a \cdot (b + c) = a \cdot b + a \cdot c$
$a \cdot (b - c) = a \cdot b - a \cdot c$

für alle a, b, c,

\in

Q

$\frac{b+c}{a}$ = $\frac{b}{a}$ + $\frac{c}{a}$ bzw.

(b + c) : a = b : a + c : a

$\frac{b-c}{a}$ = $\frac{b}{a}$ - $\frac{c}{a}$ bzw.

(b - c) : a = b : a - c : a

für alle a, b, c,

\in Q; (a \neq  0)

Klammerregeln

$a + (b + c) = a + b + c$
$a + (b - c) = a + b - c$
$a - (b + c) = a - b - c$
$a - (b - c) = a - b + c$
$(a + b) \cdot (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd$
$(a - b) \cdot (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd$
$(a + b) \cdot (c - d) = a(c - d) + b(c - d) = ac - ad + bc - bd$
$(a - b) \cdot (c - d) = a(c - d) - b(c - d) = ac - ad - bc + bd$

Terme

Mathematik-digital.de

@@ Zeile 13: / Zeile 13: @@
 '''Termart''': Die Termart wird durch das letzte ausgeführte Rechenzeichen festgelegt. ([[Terme/Terme_und_Variablen/Termarten|mehr Information]])
 ==Rechengesetze==
 '''Kommutativgesetz'''
-* <math> a + b = b + a </math>
-* <math> a \cdot b = b \cdot a </math>
+*<math> a + b = b + a </math>
-: für alle a, b, c <math>\in Q</math>
+*<math> a \cdot b = b \cdot a </math>
+:für alle a, b, c <math>\in Q</math>
 <br />
 '''Assoziativgesetz'''
-* <math> a + (b + c) = (a + b) + c = a + b + c </math>
-* <math> a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c </math>
+*<math> a + (b + c) = (a + b) + c = a + b + c </math>
-: für alle a, b, c <math>\in Q</math>
+*<math> a \cdot (b \cdot c) = (a \cdot b) \cdot c = a \cdot b \cdot c </math>
+:für alle a, b, c <math>\in Q</math>
 <br />
 '''Distributivgesetz'''
@@ Zeile 31: / Zeile 36: @@
 <div class="grid">
   <div class="width-1-2">
-* <math> a \cdot (b + c) = a \cdot b + a \cdot c </math>
+*<math> a \cdot (b + c) = a \cdot b + a \cdot c </math>
-* <math> a \cdot (b - c) = a \cdot b - a \cdot c </math>
+*<math> a \cdot (b - c) = a \cdot b - a \cdot c </math>
-: für alle a, b, c, <math>\in</math> <math>Q</math></div>
+:für alle a, b, c, <math>\in</math> <math>Q</math></div>
   <div class="width-1-2">
-* <math>\frac{b+c}{a}</math> = <math>\frac{b}{a}</math> + <math>\frac{c}{a}</math>  &nbsp; bzw.
+*<math>\frac{b+c}{a}</math> = <math>\frac{b}{a}</math> + <math>\frac{c}{a}</math>  &nbsp; bzw.
-: <math> (b + c) : a = b : a + c : a </math>
-* <math>\frac{b-c}{a}</math> = <math>\frac{b}{a}</math> - <math>\frac{c}{a}</math>  &nbsp; bzw.
+:<math> (b + c) : a = b : a + c : a </math>
-: <math> (b - c) : a = b : a - c : a </math>
+*<math>\frac{b-c}{a}</math> = <math>\frac{b}{a}</math> - <math>\frac{c}{a}</math>  &nbsp; bzw.
+:<math> (b - c) : a = b : a - c : a </math>
 :für alle a, b, c, <math>\in Q; (a \neq  0) </math>
   </div>
@@ Zeile 45: / Zeile 54: @@
 ==Klammerregeln==
-* <math> a + (b + c) = a + b + c </math>
-* <math> a + (b - c) = a + b - c </math>
-* <math> a - (b + c) = a - b - c </math>
-* <math> a - (b - c) = a - b + c </math>
-* <math> (a + b) \cdot (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd </math>
-* <math> (a - b) \cdot (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd </math>
-* <math> (a + b) \cdot (c - d) = a(c - d) + b(c - d) = ac - ad + bc - bd </math>
-* <math> (a - b) \cdot (c - d) = a(c - d) - b(c - d) = ac - ad - bc + bd </math>
+*<math> a + (b + c) = a + b + c </math>
+*<math> a + (b - c) = a + b - c </math>
+*<math> a - (b + c) = a - b - c </math>
+*<math> a - (b - c) = a - b + c </math>
+*<math> (a + b) \cdot (c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd </math>
+*<math> (a - b) \cdot (c + d) = a(c + d) - b(c + d) = ac + ad - bc - bd </math>
+*<math> (a + b) \cdot (c - d) = a(c - d) + b(c - d) = ac - ad + bc - bd </math>
+*<math> (a - b) \cdot (c - d) = a(c - d) - b(c - d) = ac - ad - bc + bd </math>
 {{Lernpfad Terme}}
-[[Kategorie:ZUM2Edutags]]
-[[Kategorie:Mathematik]]
 [[Kategorie:Terme]]

Suche

Terme/Grundwissenübersicht - Alles auf einen Blick: Unterschied zwischen den Versionen

Aktuelle Version vom 23. April 2022, 16:07 Uhr

Begriffe

Rechengesetze

Klammerregeln

Navigation

Fächer

Hilfen

⧼advertisement⧽

Suche

Terme/Grundwissenübersicht - Alles auf einen Blick: Unterschied zwischen den Versionen

Aktuelle Version vom 23. April 2022, 16:07 Uhr

Begriffe

Rechengesetze

Klammerregeln

Navigation

⧼advertisement⧽

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge