Terme/Multiplizieren und Dividieren von Summen und Differenzen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (13 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Flächeninhalt eines Rechtecks lautet <math> A_R= | Der Flächeninhalt eines Rechtecks lautet <math> A_R= l \cdot b </math> | ||
Die Länge l setzt sich hier aus a+e zusammen, b ist in diesem Fall s. <br /> | Die Länge l setzt sich hier aus a+e zusammen, b ist in diesem Fall s. <br /> | ||
Also errechnet sich der Flächeninhalt der Figur so: <br /> | Also errechnet sich der Flächeninhalt der Figur so: <br /> | ||
<math> A_F = ( | <math> A_F = ( a+e ) \cdot s </math>}} | ||
}} | |||
<br /> | <br /> | ||
Überlege nun, wie du das Produkt in eine Summe umwandeln kannst. | Überlege nun, wie du das Produkt in eine Summe umwandeln kannst. | ||
| Zeile 31: | Zeile 30: | ||
Man multipliziert eine Summe (bzw. Differenz) mit einem Faktor, indem man jedes Glied der Summe (bzw. Differenz) mit dem Faktor multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). | Man multipliziert eine Summe (bzw. Differenz) mit einem Faktor, indem man jedes Glied der Summe (bzw. Differenz) mit dem Faktor multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). | ||
: <math> a \cdot(b+c) = a \cdot b+a \cdot c = ab + ac \text{ für alle } a, b, c \in Q</math> | :<math> a \cdot(b+c) = a \cdot b+a \cdot c = ab + ac \text{ für alle } a, b, c \in Q</math> | ||
: <math> a \cdot (b-c) = a \cdot b - a \cdot c = ab - ac \text{ für alle } a, b, c \in Q</math> | :<math> a \cdot (b-c) = a \cdot b - a \cdot c = ab - ac \text{ für alle } a, b, c \in Q</math> | ||
:: (Vorgehensweise nach dem Distributivgesetz der Multiplikation) | ::(Vorgehensweise nach dem Distributivgesetz der Multiplikation) | ||
| Zeile 45: | Zeile 41: | ||
Multipliziere nun folgende Terme aus: | Multipliziere nun folgende Terme aus: | ||
* <math> (4+m)\cdot 2 </math> | *<math> (4+m)\cdot 2 </math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> (4+m)\cdot 2 = 4 \cdot 2 + m \cdot 2 = 8 +2m </math> | <math> (4+m)\cdot 2 = 4 \cdot 2 + m \cdot 2 = 8 +2m </math> | ||
| Zeile 51: | Zeile 47: | ||
}} | }} | ||
* <math> (7+z) \cdot (-4) </math> | *<math> (7+z) \cdot (-4) </math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> (7+z)\cdot (-4) = 7\cdot (-4) + z\cdot (-4) = -28 - 4z </math> | <math> (7+z)\cdot (-4) = 7\cdot (-4) + z\cdot (-4) = -28 - 4z </math> | ||
| Zeile 57: | Zeile 53: | ||
}} | }} | ||
* <math> (\frac{1}{2}+a) \cdot \frac{1}{2}</math> | *<math> (\frac{1}{2}+a) \cdot \frac{1}{2}</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> (\frac{1}{2} + a) \cdot \frac{1}{2} = \frac{1}{2} \cdot \frac{1}{2} + a \cdot \frac{1}{2} = </math> | <math> (\frac{1}{2} + a) \cdot \frac{1}{2} = \frac{1}{2} \cdot \frac{1}{2} + a \cdot \frac{1}{2} = </math> | ||
| Zeile 65: | Zeile 61: | ||
}} | }} | ||
* <math> (\frac{1}{3}-k) \cdot \frac{3}{4}</math> | *<math> (\frac{1}{3}-k) \cdot \frac{3}{4}</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> (\frac{1}{3}- k) \cdot \frac{3}{4} = \frac{1}{3}\cdot \frac{3}{4} - k \cdot \frac{3}{4} = </math> | <math> (\frac{1}{3}- k) \cdot \frac{3}{4} = \frac{1}{3}\cdot \frac{3}{4} - k \cdot \frac{3}{4} = </math> | ||
| Zeile 112: | Zeile 108: | ||
Man dividiert eine Summe (oder Differenz) durch einen von null verschiedenen Divisor, indem man jedes Glied der einen Summe (bzw. Differenz) durch den Divisor teilt und die entstandenen Quotienten addiert (bzw. subtrahiert). | Man dividiert eine Summe (oder Differenz) durch einen von null verschiedenen Divisor, indem man jedes Glied der einen Summe (bzw. Differenz) durch den Divisor teilt und die entstandenen Quotienten addiert (bzw. subtrahiert). | ||
: <math>\frac{a+b}{c} = \frac{a}{c}+ \frac{b}{c} \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | :<math>\frac{a+b}{c} = \frac{a}{c}+ \frac{b}{c} \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | ||
bzw.: | bzw.: | ||
: | :<math> (a+b):c = a:c + b:c \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | ||
: <math> \frac{a-b}{c} = \frac{a}{c} - \frac{b}{c} \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | :<math> \frac{a-b}{c} = \frac{a}{c} - \frac{b}{c} \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | ||
bzw.: | bzw.: | ||
: | :<math> (a-b):c = a:c - b:c \text{ für a, b } \in Q ; c \in Q \setminus \{0\} </math> | ||
:: (Vorgehensweise nach dem Distributivgesetz der Division) | ::(Vorgehensweise nach dem Distributivgesetz der Division) | ||
| Zeile 136: | Zeile 131: | ||
Dividiere selbst: | Dividiere selbst: | ||
* <math> (z-0,5):2 </math> | *<math> (z-0,5):2 </math> | ||
* <math> (m-c):c </math> | *<math> (m-c):c </math> | ||
* <math> (2,8-0,3):a </math> | *<math> (2,8-0,3):a </math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 160: | Zeile 155: | ||
Wie oben: | Wie oben: | ||
<math> A_F = ( | <math> A_F = ( a+e ) \cdot s </math> | ||
für <math> s = a+f </math> einsetzen: | für <math> s = a+f </math> einsetzen: | ||
<math> A_F = ( | <math> A_F = ( a+e ) \cdot ( a + f ) </math> | ||
}} | }} | ||
| Zeile 183: | Zeile 178: | ||
Man multipliziert zwei Summen (bzw. Differenzen) miteinander, indem man jedes Glied der einen Summe (bzw. Differenz) mit jedem Glied der anderen Summe (bzw. Differenz) multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). Dieser Rechenschritt verwandelt ein <u>Produkt in eine Summe</u>. | Man multipliziert zwei Summen (bzw. Differenzen) miteinander, indem man jedes Glied der einen Summe (bzw. Differenz) mit jedem Glied der anderen Summe (bzw. Differenz) multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). Dieser Rechenschritt verwandelt ein <u>Produkt in eine Summe</u>. | ||
: <math> (a+b) \cdot (c+d) = a(c+d) + b(c+d) = (ac+ad) + (bc+bd) = ac + ad + bc + bd </math> | :<math> (a+b) \cdot (c+d) = a(c+d) + b(c+d) = (ac+ad) + (bc+bd) = ac + ad + bc + bd </math> | ||
: <math> (a-b) \cdot (c+d) = a(c+d) - b(c+d) = (ac+ad) - (bc+bd) = ac + ad - bc - bd </math> | :<math> (a-b) \cdot (c+d) = a(c+d) - b(c+d) = (ac+ad) - (bc+bd) = ac + ad - bc - bd </math> | ||
: <math> (a+b) \cdot (c-d) = a(c-d) + b(c-d) = (ac-ad) + (bc-bd) = ac - ad + bc - bd </math> | :<math> (a+b) \cdot (c-d) = a(c-d) + b(c-d) = (ac-ad) + (bc-bd) = ac - ad + bc - bd </math> | ||
: <math> (a-b) \cdot (c-d) = a(c-d) - b(c-d) = (ac-ac) - (bc-bd) = ac - ad - bc + bd </math | :<math> (a-b) \cdot (c-d) = a(c-d) - b(c-d) = (ac-ac) - (bc-bd) = ac - ad - bc + bd </math> | ||
<u>Achte auf die Vor- und Rechenzeichen!</u> | |||
| Zeile 199: | Zeile 191: | ||
Berechne selbst: | Berechne selbst: | ||
* <math> (y+7)(3+y | |||
*<math> (y+7)(3+y) </math> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
* <math> (y+7)(3+y) = y(3+y) + 7(3+y) = (3y+y^2) + (21+7y) </math> | * <math> (y+7)(3+y) = y(3+y) + 7(3+y) = (3y+y^2) + (21+7y) </math> | ||
:<math>= 3y+y^2 + 21 +7y = y^2 +10y+21 </math>}} | |||
<math> | *<math> (a-5)(1+a+2) </math> | ||
{{Lösung versteckt|1= | |||
* <math> (a-5)(1+a+2) = a(1+a+2) - 5(1+a+2) = (a+a^2+2a) - (5+5a+10) </math> | * <math> (a-5)(1+a+2) = a(1+a+2) - 5(1+a+2) = (a+a^2+2a) - (5+5a+10) </math> | ||
:<math> = a+a^2+2a-5-5a-10 = a^2+a+2a-5a-5-10 = a^2-2a-15 </math>}} | |||
<math> | *<math> (m+n+o)(m-n-o) </math> | ||
{{Lösung versteckt|1= | |||
* <math> (m+n+o)(m-n-o) = m(m-n-o) + n(m-n-o) + o(m-n-o) </math> | * <math> (m+n+o)(m-n-o) = m(m-n-o) + n(m-n-o) + o(m-n-o) </math> | ||
:<math> = (m^2-mn-mo) + (mn-n^2-no) + (mo-no-o^2) </math> | |||
<math> = (m^2-mn-mo) + (mn-n^2-no) + (mo-no-o^2) </math> | :<math> = m^2-mn-mo+mn-n^2-no+mo-no-o^2 = m^2-n^2-2no-o^2 </math>}} | ||
<math> = m^2-mn-mo+mn-n^2-no+mo-no-o^2 = m^2-n^2-2no-o^2 </math> | |||
}} | |||
| Zeile 243: | Zeile 233: | ||
Dieser Rechenschritt verwandelt eine <u>Summe in ein Produkt</u>. | Dieser Rechenschritt verwandelt eine <u>Summe in ein Produkt</u>. | ||
: | :<math> a \cdot b + a \cdot c + a \cdot d + a \cdot e = a \cdot (b+c+d+e) </math> | ||
| Zeile 255: | Zeile 242: | ||
Berechne selbst: | Berechne selbst: | ||
* <math> ax+a </math> | *<math> ax+a </math> | ||
* <math> 6z^2 + 21z </math> | *<math> 6z^2 + 21z </math> | ||
* <math> 6ab^3 + 9ab^2 - 15ab </math> | *<math> 6ab^3 + 9ab^2 - 15ab </math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 291: | Zeile 278: | ||
* <math> (5r+2)(3r+2) = 5r(3r+2) + 2(3r+2) = (15r^2+10r) + (6r+4) </math> | * <math> (5r+2)(3r+2) = 5r(3r+2) + 2(3r+2) = (15r^2+10r) + (6r+4) </math> | ||
<math> = 15r^2 | <math> = 15r^2 +10r+6r+4 = 15r^2+16r+4 </math> | ||
}} | }} | ||
| Zeile 306: | Zeile 293: | ||
}} | }} | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
| Zeile 318: | Zeile 304: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
a) <math> A = (3x+y) \cdot (3x+y) = 3x(3x+y) + y(3x+y) = (9x^2+3xy) + (3xy+y^2) </math> | a) <math> | ||
\begin{array}{lcr} | |||
A & = & (3x+y) \cdot (3x+y) \\ | |||
& = & 3x(3x+y) + y(3x+y)\\ | |||
& = & (9x^2+3xy) + (3xy+y^2) \\ | |||
& = & 9x^2+3xy+3xy+y^2 \\ | |||
&= & 9x^2+6xy+y^2 | |||
\end{array} | |||
</math> | |||
b) <math> A = (2a+3b) \cdot (2a-3b) = 2a(2a-3b) + 3b(2a-3b) = (4a^2-6ab) + (6ab-9b^2) </math> | b) <math> A = (2a+3b) \cdot (2a-3b) = 2a(2a-3b) + 3b(2a-3b) = (4a^2-6ab) + (6ab-9b^2) </math> | ||
| Zeile 336: | Zeile 328: | ||
{{{!}} class="wikitable center" | {{{!}} class="wikitable center" | ||
{{!}}- | {{!}}- | ||
! (x+2) | ! <math> (x+2) \cdot (x+3) </math> !! <math> (x-3) \cdot (x-1) </math> !! <math> (x-5) \cdot (x+2) </math> !! <math> (x+4) \cdot (x-2) </math> !! <math> (x-1) \cdot(x+1) </math> !! <math> (x+2) \cdot (x+2) </math> | ||
{{!}}- | {{!}}- | ||
{{!}} <strong> x<sup>2</sup> +5x+6 </strong> {{!}}{{!}} <strong> x<sup>2</sup> -4x+3 </strong> {{!}}{{!}} <strong> x<sup>2</sup>-3x-10 </strong> {{!}}{{!}} <strong> x<sup>2</sup>+2x-8 </strong> {{!}}{{!}} <strong> x<sup>2</sup> -1 </strong> {{!}}{{!}} <strong> x<sup>2</sup>+4x+4 </strong> | {{!}} <strong> x<sup>2</sup> +5x+6 </strong> {{!}}{{!}} <strong> x<sup>2</sup> -4x+3 </strong> {{!}}{{!}} <strong> x<sup>2</sup>-3x-10 </strong> {{!}}{{!}} <strong> x<sup>2</sup>+2x-8 </strong> {{!}}{{!}} <strong> x<sup>2</sup> -1 </strong> {{!}}{{!}} <strong> x<sup>2</sup>+4x+4 </strong> | ||
| Zeile 344: | Zeile 336: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
Super! Den Hauptteil des Lernpfades hast du geschafft!! | |||
{{Fortsetzung|weiter=Weiteren Aufgaben zum Üben!|weiterlink=../weitere Aufgaben}} | |||
[[Kategorie:Variable]] | |||
[[Kategorie:Terme]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 16:05 Uhr
Distributivgesetz der Multiplikation
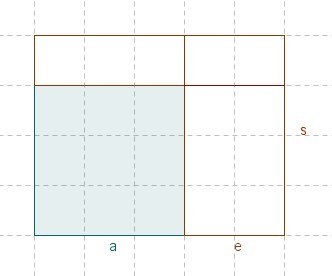
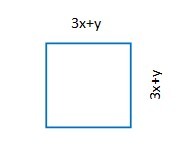
Ein Quadrat der Kantenlänge a wird auf der einen Seite um e erweitert und auf der anderen Seite zur Seitenlänge s erweitert (siehe Skizze). Wie errechnest du den Flächeninhalt des neuen Rechtecks?
Der Flächeninhalt eines Rechtecks lautet
Die Länge l setzt sich hier aus a+e zusammen, b ist in diesem Fall s.
Also errechnet sich der Flächeninhalt der Figur so:
Überlege nun, wie du das Produkt in eine Summe umwandeln kannst.
Erklärung
Man multipliziert eine Summe (bzw. Differenz) mit einem Faktor, indem man jedes Glied der Summe (bzw. Differenz) mit dem Faktor multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert).
-
- (Vorgehensweise nach dem Distributivgesetz der Multiplikation)
Beispiel
Multipliziere nun folgende Terme aus:
Distributivgesetz der Division
Anna, Sara und Kerstin haben eine Tüte Bonbons geschenkt bekommen. Die Tüte enthält 9 Waldbeerbonbons und 18 Kirschbonbons. Die drei Freundinnen wollen die Bonbons gerecht untereinander aufteilen. Jede macht einen Vorschlag:
- Anna: "Wir zählen alle Bonbons zusammen und teilen sie dann durch 3."
- Sara: "Wir teilen erst die Waldbeerbonbons durch 3, dann die Kirschbonbons und zählen dann zusammen, wie viele Bonbons jede von uns bekommt."
- Kerstin: "Ist es nicht egal, ob wir erst zusammenzählen und dann teilen oder erst teilen und dann zusammenzählen?"
Was meinst du? Schreibe die beiden Rechenvorschriften als Termen und prüfe, welche der drei Mädchen recht hat.
- Anna:
- Sara:
Also haben alle drei Freundinnen recht.
Versuche nun, eine dafür allgemein geltende Rechenregel zu formulieren.
Erklärung
Man dividiert eine Summe (oder Differenz) durch einen von null verschiedenen Divisor, indem man jedes Glied der einen Summe (bzw. Differenz) durch den Divisor teilt und die entstandenen Quotienten addiert (bzw. subtrahiert).
bzw.:
bzw.:
- (Vorgehensweise nach dem Distributivgesetz der Division)
Beispiel
Dividiere selbst:
Ausmultiplizieren und Ausklammern
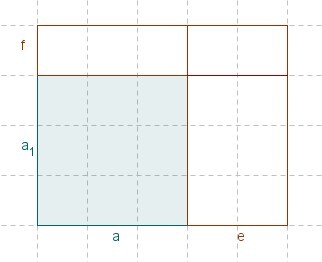
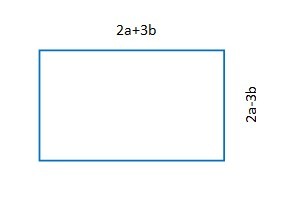
Du hast vorhin ein Quadrat berechnet, dessen Seitenlänge a um e erweitert wurde und dessen andere Seitenlänge zu s erweitert wurde. Berechne jetzt den Flächeninhalt für das Rechteck, wenn sich s aus a und f zusammensetzt. (siehe Skizze)
Wie oben:
für einsetzen:
Mit Hilfe des Distributivgesetzes kannst du eine Summe mit einem Faktor multiplizieren (bzw. dividieren). Überlege, wie der neue Term für den Flächeninhalt ausmultipliziert werden kann.
Erklärung
Man multipliziert zwei Summen (bzw. Differenzen) miteinander, indem man jedes Glied der einen Summe (bzw. Differenz) mit jedem Glied der anderen Summe (bzw. Differenz) multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). Dieser Rechenschritt verwandelt ein Produkt in eine Summe.
Achte auf die Vor- und Rechenzeichen!
Beispiel
Berechne selbst:
Wende das Distributivgesetz an, um aus einer Summe ein Produkt zu machen.
Erklärung
Enthält in einer Summe aus Produkten jedes Produkt einen oder mehrere gemeinsame Faktoren, so kann man diese nach dem Distributivgesetz ausklammern.
Dieser Rechenschritt verwandelt eine Summe in ein Produkt.
Beispiel
Berechne selbst:
Übungsaufgaben
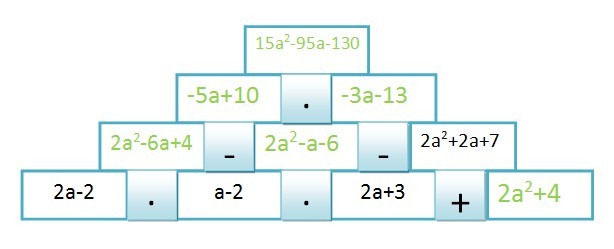
Multipliziere aus und fasse zusammen
Finde die Lösungen und ziehe sie mit der Maus in das Lösungsfeld.
| x2 +5x+6 | x2 -4x+3 | x2-3x-10 | x2+2x-8 | x2 -1 | x2+4x+4 |
Super! Den Hauptteil des Lernpfades hast du geschafft!!