Achsensymmetrie: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Achsensymmetrie,Mathematik,Lernpfad,5. Klasse</metakeywords>Kategorie:ZUM2Edutags {{Lernpfad-M| {{K…“) Markierung: Quelltext-Bearbeitung 2017 |
K (- ZUM2Edutags) Markierung: Quelltext-Bearbeitung 2017 |
||
| (94 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|Lernpfad| | |||
* Zeitbedarf: 40 Minuten | |||
* Material: Computer und Heft | |||
[[Datei:Logo Mathematik-digital 2011.png|200px|right|verweis=Mathematik-digital|Mathematik-digital]] | |||
|Lernpfad}} | |||
__NOTOC__ | |||
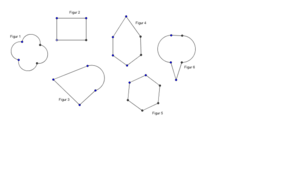
[[Bild:Figuren1.png|thumb|Verschiedene Figuren]] | == Aufgabe 1 == | ||
{{Box|1=Übung | 2=[[Bild:Figuren1.png|thumb|Verschiedene Figuren]] | |||
Schaut euch die Figuren an und überlegt, ob an ihnen etwas besonders ist. Klickt auf das Bild zum Vergrößern. | |||
(''Hinweis:'' Die gesuchte "Besonderheit" findet ihr in Figur 3 '''nicht'''.) | (''Hinweis:'' Die gesuchte "Besonderheit" findet ihr in Figur 3 '''nicht'''.) | ||
Zeichnet Figur 1 und Figur 4 in euer Heft und überlegt, ob es Geraden gibt mit denen ihr die Figuren so teilen könnt, dass sie aufeinanderliegen. | |||
Ihr könnt auch versuchen, die Figuren aus einem Blatt Papier auszuschneiden, und sie so zu falten, dass keine Seite unter der anderen hervorragt. Öffnet das Papier wieder, nachdem euch das gelungen ist und betrachtet die Linie der Faltkante. Sie sollte genauso verlaufen wie die Geraden in eurem Heft. | Ihr könnt auch versuchen, die Figuren aus einem Blatt Papier auszuschneiden, und sie so zu falten, dass keine Seite unter der anderen hervorragt. Öffnet das Papier wieder, nachdem euch das gelungen ist und betrachtet die Linie der Faltkante. Sie sollte genauso verlaufen wie die Geraden in eurem Heft. | ||
|3=Üben}} | |||
{{Box | |||
|Merksatz | |||
|Die Gerade, die eine Figur deckungsgleich halbiert, heißt '''Symmetrieachse'''. | |||
Gibt es mindestens eine solche Achse, heißt die Figur achsensymmetrisch. | |||
|Merksatz | |||
}} | |||
== Aufgabe 2 == | == Aufgabe 2 == | ||
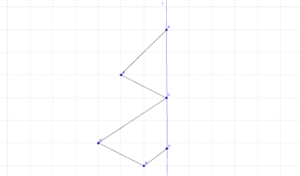
[[Bild:Spieg111.png|300px| | {{Übung|1=[[Bild:Spieg111.png|300px|thumb]] Zeichnet die nebenstehende Figur in euer Heft ab und ergänzt sie mit Hilfe der eingezeichneten Symmetrieachse (<span style="color:blue">blaue</span> Gerade). Unter Anzeigen findet ihr die Lösung. | ||
}} | |||
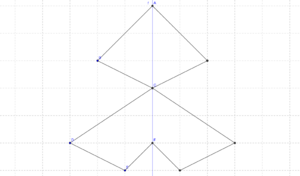
{{Lösung versteckt|Lösung: [[Bild:Spieg1lös.png|300px|thumb|center]] | |||
}} | |||
---- | |||
{{ | {{Übung|1= | ||
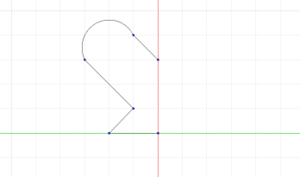
[[Bild: | [[Bild:Spieg2.png|300px|thumb]]Zeichnet nun die nebenstehende Figur ab und ergänzt sie. Spiegelt die Figur hierfür zuerst an der <span style="color:red">roten</span> Symmetrieachse und dann an der <span style="color:green">grünen</span>. Klickt anschließend auf "Lösung anzeigen" um zu sehen, ob ihr es richtig gemacht habt. | ||
}} | }} | ||
{{Lösung versteckt|Lösung: [[Bild:Spieg2lös.png|300px|thumb|center]] | |||
{{versteckt| | |||
[[Bild:Spieg2lös.png|300px|center]] | |||
}} | }} | ||
---- | |||
== Aufgabe 3 == | == Aufgabe 3 == | ||
[[Bild:Figuren1.png|right|Verschiedene Figuren]] | |||
<quiz display="simple"> | <quiz display="simple"> | ||
{ Wie viele Symmetrieachsen haben sie? | { Wie viele Symmetrieachsen haben sie? | ||
| typ="()" } | | typ="()" } | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
----+-- Figur 1 | ----+-- Figur 1 | ||
--+---- Figur 2 | --+---- Figur 2 | ||
| Zeile 73: | Zeile 58: | ||
------+ Figur 5 | ------+ Figur 5 | ||
-+----- Figur 6 | -+----- Figur 6 | ||
</quiz> | </quiz> | ||
== Aufgabe 4 == | == Aufgabe 4 == | ||
In diesem Geogebra-Applet seht ihr zwei zueinander senkrechte Symmetrieachsen. Bewegt die beschrifteten Punkte. Was passiert bezüglich der Symmetrie? | In diesem Geogebra-Applet seht ihr zwei zueinander senkrechte Symmetrieachsen. Bewegt die beschrifteten Punkte. Was passiert bezüglich der Symmetrie? | ||
<ggb_applet height="400" width="500" showMenuBar="false" showResetIcon="true" filename="Achsensymmetrie2.ggb" /> | <ggb_applet height="400" width="500" showMenuBar="false" showResetIcon="true" filename="Achsensymmetrie2.ggb" /> | ||
== Aufgabe 5 == | == Aufgabe 5 == | ||
Nun betrachten wir regelmäßige Vielecke (d.h. Vielecke, in denen alle Winkel und alle Seiten gleich sind). | Nun betrachten wir regelmäßige Vielecke (d.h. Vielecke, in denen alle Winkel und alle Seiten gleich sind). | ||
In folgender Tabelle seht ihr, wie viele Symmetrieachsen ein regelmäßiges Vieleck hat: | In folgender Tabelle seht ihr, wie viele Symmetrieachsen ein regelmäßiges Vieleck hat: | ||
| Zeile 124: | Zeile 100: | ||
Erstellt euch mit Geogebra regelmäßige Vielecke und versucht alle Symmetrieachsen zu finden. | Erstellt euch mit Geogebra regelmäßige Vielecke und versucht alle Symmetrieachsen zu finden. | ||
'''Zusatzaufgabe''': | |||
Findet ein geometrisches Objekt mit unendlich vielen Symmetrieachsen! | Findet ein geometrisches Objekt mit unendlich vielen Symmetrieachsen! | ||
== Aufgabe 6 == | == Aufgabe 6 == | ||
<quiz> | <quiz> | ||
| Zeile 159: | Zeile 133: | ||
+ Falsch | + Falsch | ||
</quiz> | </quiz> | ||
== Links == | == Links == | ||
| Zeile 165: | Zeile 140: | ||
* [http://de.wikipedia.org/wiki/Achsensymmetrie#Achsensymmetrie Wikipedia] | * [http://de.wikipedia.org/wiki/Achsensymmetrie#Achsensymmetrie Wikipedia] | ||
* [http://www.didaktik.mathematik.uni-wuerzburg.de/projekt/mathei/symmetrie/symdef1.html Didaktik der Mathematik (Universität Würzburg)] | * [http://www.didaktik.mathematik.uni-wuerzburg.de/projekt/mathei/symmetrie/symdef1.html Didaktik der Mathematik (Universität Würzburg)] | ||
* [[dmuw:Lernpfade/Symmetrie]] | |||
Hier findet ihr das Programm [ | Hier findet ihr das Programm [https://www.geogebra.org/ Geogebra] mit dem die auf dieser Seite verwendeten Bilder erstellt worden sind. Es handelt sich dabei um ein sehr hilfreiches Programm, das euch helfen kann, Geometrie besser zu verstehen. | ||
{{Autoren|Martina Ott, Christoph Lembach, Angela Röhrig, Manuel Schüttler, Milena Tieves}} | |||
__NOEDITSECTION__ | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Achsensymmetrie]] | [[Kategorie:Achsensymmetrie]] | ||
[[Kategorie: | [[Kategorie:Lernpfad]] | ||
[[Kategorie:Mathematik-digital]] | |||
[[ | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 17. Dezember 2021, 10:35 Uhr
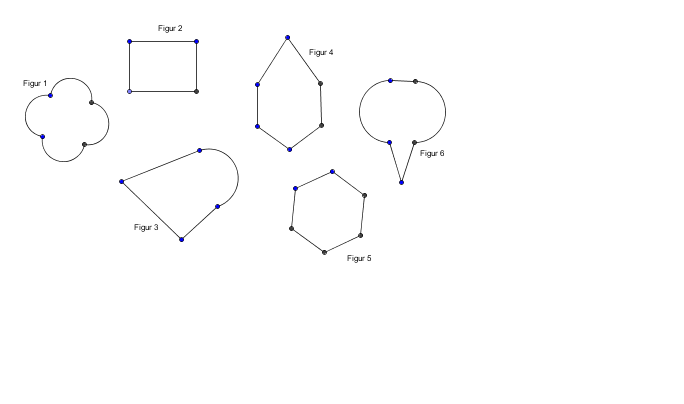
Aufgabe 1
Schaut euch die Figuren an und überlegt, ob an ihnen etwas besonders ist. Klickt auf das Bild zum Vergrößern.
(Hinweis: Die gesuchte "Besonderheit" findet ihr in Figur 3 nicht.)
Zeichnet Figur 1 und Figur 4 in euer Heft und überlegt, ob es Geraden gibt mit denen ihr die Figuren so teilen könnt, dass sie aufeinanderliegen.
Ihr könnt auch versuchen, die Figuren aus einem Blatt Papier auszuschneiden, und sie so zu falten, dass keine Seite unter der anderen hervorragt. Öffnet das Papier wieder, nachdem euch das gelungen ist und betrachtet die Linie der Faltkante. Sie sollte genauso verlaufen wie die Geraden in eurem Heft.
Die Gerade, die eine Figur deckungsgleich halbiert, heißt Symmetrieachse.
Gibt es mindestens eine solche Achse, heißt die Figur achsensymmetrisch.
Aufgabe 2
Aufgabe 3
Aufgabe 4
In diesem Geogebra-Applet seht ihr zwei zueinander senkrechte Symmetrieachsen. Bewegt die beschrifteten Punkte. Was passiert bezüglich der Symmetrie?
Die Datei [INVALID] wurde nicht gefunden.
Aufgabe 5
Nun betrachten wir regelmäßige Vielecke (d.h. Vielecke, in denen alle Winkel und alle Seiten gleich sind). In folgender Tabelle seht ihr, wie viele Symmetrieachsen ein regelmäßiges Vieleck hat:
| Anzahl der Ecken | 3 | 4 | 5 | 6 | ... | n |
|---|---|---|---|---|---|---|
| Anzahl der Symmetrieachsen | 3 | 4 | 5 | 6 | ... | n |
| Winkel | 3 mal 60° | 4 mal 90° | 5 mal 108° | 6 mal 120° | ... | n mal 180°*(n-2)/n |
Erstellt euch mit Geogebra regelmäßige Vielecke und versucht alle Symmetrieachsen zu finden.
Zusatzaufgabe:
Findet ein geometrisches Objekt mit unendlich vielen Symmetrieachsen!
Aufgabe 6
Links
Hier findet ihr noch mehr zum Thema Achsensymmetrie:
Hier findet ihr das Programm Geogebra mit dem die auf dieser Seite verwendeten Bilder erstellt worden sind. Es handelt sich dabei um ein sehr hilfreiches Programm, das euch helfen kann, Geometrie besser zu verstehen.