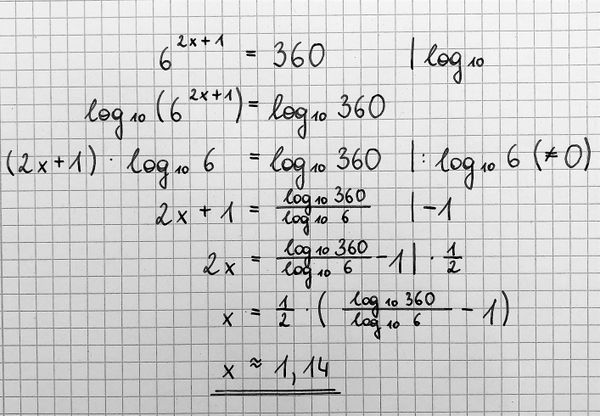Benutzer:Christian/test-2

Erdbeben und Logarithmus

1. Entstehung von Erdbeben
2. Erdbeben in Österreich
3. Stärke von Erdbeben
4. Der Logarithmus
5. Logarithmische Skalen
6. Verhalten bei einem Erdbeben
7. Tsunamis (Optional)
8. Abschluss

Im letzten Kapitel bist du bereits auf die Magnitude gestoßen. Es ist in der Tat so, dass bei einem Beben der Magnitude 6,8 um ein Vielfaches mehr Energie freigesetzt wird, als bei einem der Magnitude 5,8. Das erklärt den Unterschied im Zerstörungspotential zwischen den Erdbeben 2020 in der Türkei. Steigt die Richter-Magnitude um 1, entspricht das einer Ver-32-fachung der freigesetzten Energiemenge. Bei einer Richter-Magnitude von 5,0 werden beispielsweise 10¹² Joule freigesetzt. Bei 6,0 sind es bereits 2,5 $\cdot$ 10¹³ Joule und bei 7,0 beträgt die Energiefreisetzung 10¹⁵ Joule.

Wie genau die Richter-Magnitude definiert ist und was das mit dem Logarithmus zu tun hat, erfährst du hier in diesem Abschnitt.

Merke: Exponentialgleichungen

Du kannst bereits lineare oder quadratische Gleichungen lösen. Aber was ist, wenn die Unbekannte plötzlich im Exponenten steht? - Alles kein Problem mit dem Logarithmus!

Wir versuchen nun, die Gleichung $6^{2x+1} = 360$ für $x \in \mathbb{R}$ näherungsweise zu lösen.

Dabei gehen wir folgendermaßen vor: Wir logarithmieren die Gleichung, das heißt, wir wenden den Logarithmus auf beiden Seiten an. Die Basis des Logarithmus können wir beliebig wählen (Exponentialgleichungen mit der Basis $e$ löst man am einfachsten mit dem natürlichen Logarithmus.). In unserem Fall verwenden wir den dekadischen Logarithmus. Anschließend benutzen wir die Rechenregeln für Logarithmen. Durch weitere Äquivalenzumformungen und mit Technologieeinsatz können wir die Gleichung näherungsweise lösen.

Stärke von Erdbeben

Logarithmische Skalen

Erstellt von: Lisa Birglechner (Diskussion)

Autor*innen

aktualisiert am: