Benutzer:Wilke de Vries/Muster erkennen und geschickt fortsetzen

Quadratische Funktionen erkunden

• Wiederholung
• Quadratische Funktionen im Alltag
• Quadratische Funktionen kennenlernen
• Die Parameter der Scheitelpunktform
• Die Scheitelpunktform
• Die Parameter der Normalform
• Die Normalform
• Von der Scheitelpunkt- zur Normalform
• Übungen

< Mathematik-digital

Einführung

Regelmäßige Muster findest du oft in der Natur zum Beispiel bei Pflanzen oder auch in der regelmäßigen Struktur von Bienenwaben. Aber nicht nur Tiere folgen einem festen Bauplan, auch wir bauen "Muster" in unsere Behausungen. Da überrascht es nicht, dass schon viele Mathematiker solche Muster untersuchten und mit Zahlen beschrieben. Ein besonders bekannter Mathematiker , der sich für solche Regelmäßigkeiten interessierte, war Fibonacci. Dazu werdet ihr hier später aber noch mehr lernen!

• 

  regelmäßige Blüte

• 

  Schafgarbenblüten

• 

  Bienenwabe

• 

  Mauerwerk

Auf dieser ersten Seite geht es darum, regelmäßige Muster zu untersuchen.

Erkundungsaufgabe 1: Muster aus Hölzchen

Diese Aufgabe beantwortest du in deinem Hefter.

Fabian hat das folgende Muster aus Hölzchen gelegt.

a) Wie viele Hölzchen siehst du? Beschreibe, wie du beim Zählen vorgegangen bist!

b) Findest du auch eine weitere geschickte Zählstrategie? Notiere deine Rechnung!

c) Lucio hat ein ähnliches Muster gelegt. Zeichne beide Muster in dein Heft und ergänze mindestens zwei weitere ähnliche Muster. Wie viele Hölzchen brauchst du für die Muster jeweils?

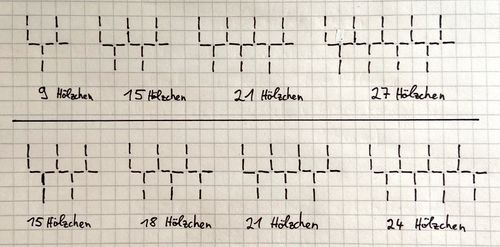
d) Berechne wie viele Hölzer du benötigst, um ein eine ähnliche Hölzchenkette mit einer Länge von 9 (oder 19) Hölzchen zu legen. Beschreibe wie du gerechnet hast!

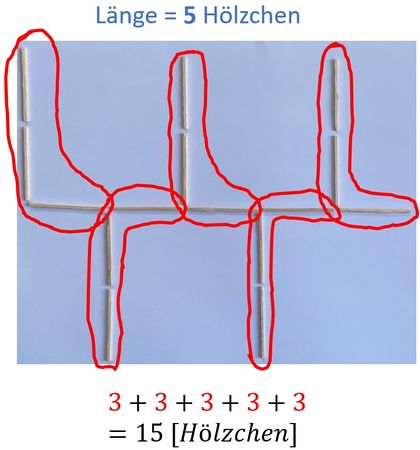
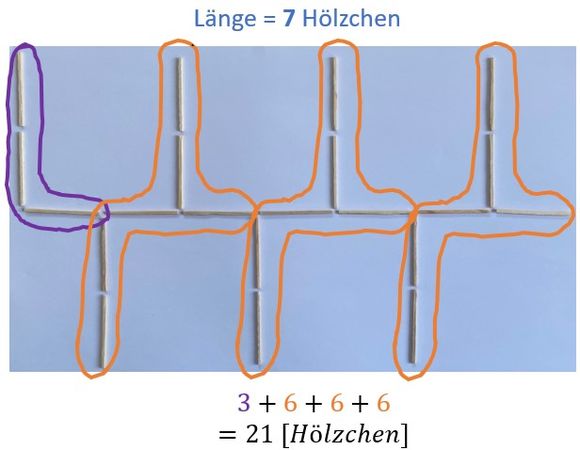
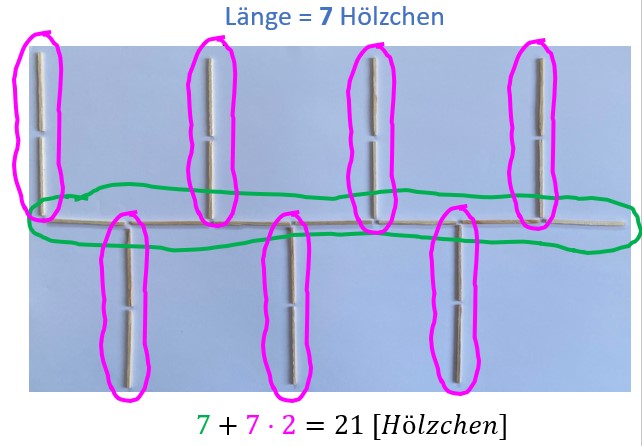
Hier kannst du dir anschauen, wie Fabian, Lucio und Merle die Hölzchen auf unterschiedliche Weise geschickt zählen. Verwende eine ähnliche Strategie, um dir zu überlegen wie viele Hölzchen du für eine Kette mit der Länge 19 benötigst.

• 

  Fabians Strategie zu zählen

• 

  Lucios Strategie zu zählen

• 

  Merles Strategie zu zählen

Fabian erklärt seine Strategie so: Ich sehe in dem Hölzchenmuster ganz viele L-förmige Muster. Für jedes "L" brauche ich 3 Hölzchen. Wenn ich 5 solche "L"-Muster aneinanderlege, brauche ich 3+3+3+3+3=15 Hölzchen.

a-b) Hier gibt es individuelle Lösungen. Zum Vergleich findest du Beispiele für Zählstratgien von Fabian und Lucio in der Hilfe zu Aufgabenteil d) - es gibt aber noch weitere Strategien!

c) Hier sind zwei Beispiele für ähnliche Bilder. Deine Lösung kann aber auch andere Muster enthalten!

d)Für eine Hölzchenkette mit einer Länge von 9 Hölzchen brauchst du insgesamt 27 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man $3+3+3+...+3=27$ oder $9\cdot3=27$.

Für eine Hölzchenkette mit einer Länge von 19 Hölzchen brauchst du insgesamt 57 Hölzchen. Wenn man so zählt wie Fabian (siehe Hilfe zu Aufgabenteil d), dann rechnet man $3+3+3+...+3=57$ oder $19\cdot3=57$.

Erkundungsaufgabe 2: Schokolinsenmuster

Merle hat Muster aus Schokolinsen gelegt. Du sollst ihr jetzt helfen die Bildmuster zu untersuchen.

a) Ordne die Bilder und Zahlen an die passenden Stellen in der Tabelle ein. Achtung: Einige Zahlen bleiben übrig und einige Bilder fehlen!

Wenn du Schwierigkeiten hast die Zahlen und die Bilder zuzuordnen, zeichne dir die gesamte Bilderfolge mit Punkten in dein Heft!

Diese Aufgabenteile b-d beantwortest du in deinem Hefter.

b) Beschreibe, wie sich die Bilder von einem Schritt zum nächsten verändern.

Beschreibe, wie sich die Zahlen von Zahl zu Zahl verändern.

Um ihre Überlegung beim Legen der Schokolinsen zu erklären, hat Merle das Muster mit farbig sortierten Schokolinsen gelegt und für jedes Bild die Anzahl der Linsen berechnet.

Erkundungsaufgabe: Schokolinsenmuster

Wie Bilder kannst du auch Zahlen in eine Reihenfolge schreiben und Regelmäßigkeiten untersuchen. Lucio hat sich eine Zahlenfolge überlegt und in die folgende Tabelle geschrieben.

c) Schreibe die Tabelle in dein Heft und ergänze zu jeder Zahl ein Bild.

d) Kannst du auch die Zahl an der 10 und 20. Stelle berechnen? Schreibe deine Rechnung auf!

Achtung:

Das solltest du beachten

Übersicht über Strategien beim geschickten Fortsetzen von Mustern