Funktion - eine eindeutige Zuordnung

Lernpfad

Funktion - eine eindeutige Zuordnung

Funktion - eine eindeutige Zuordnung

Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.

Lernziele

Den Funktionsbegriff kennen und verstehen können.

Grundkompetenzen

• FA 1.1: Für gegebene Zusammenhänge entscheiden können, ob man sie als Funktion betrachten kann.

Funktionen

Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt: "Eine Funktion ist eine eindeutige Zuordnung."

Musterbeispiel

Handel es sich bei den dargestellten Zuordnungen um Funktionen? Begründe.

1. Jedem Menschen wird seine leibliche Mutter zugeordnet.
2. Jeder Mutter wird ihr Kind zugeordnet
3. 
4. 

Lösung

1. Da jeder Mensch (Argument) nur eine leibliche Mutter (Wert) besitzt, handelt es sich bei dieser Zuordnung um eine eindeutige Zuordnung, also um eine Funktion.
2. Da eine Mutter (Argument) mehrere Kinder (Wert) haben kann, handelt es sich bei dieser Zuordnung um keine eindeutige Zuordnung, also um keine Funktion.
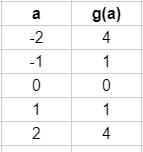
3. Da jedem Argument a genau ein Wert g(a) zugeordnet ist, handelt es sich um die Wertetabelle einer Funktion.
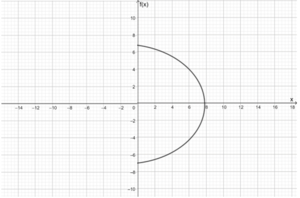
4. Da einigen Argumenten mehrere Werte zugeordnet werden, handelt es sich nicht um einen Funktionsgraphen.

Üben

Handelt es sich bei der Zuordnung (teilweise in verbaler Darstellung) um eine Funktion? Begründe!

1. Jedem in Österreich angemeldeten Auto wird eine Autonummer zugeordnet.
2. 
3. Jedem erwachsenen Österreicher wird eine Sozialversicherungsnummer zugeordnet.
4. 

Lösung

Lösung anzeigen

1. Ja, da es sich um eine eindeutige Zuordnung zwischen jedem Auto (Argument) und seinem Kennzeichen (Wert) handelt.
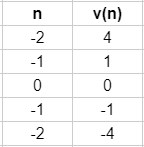
2. Nein, da einige Argumente (beispielsweise -2) zwei Werte zugeordnet werden, handelt es sich um keine Wertetabelle einer Funktion.
3. Ja, da es sich um eine eindeutige Zuordnung zwischen jedem erwachsenen Österreicher (Argument) und seiner Sozialversicherungsnummer (Wert) handelt.
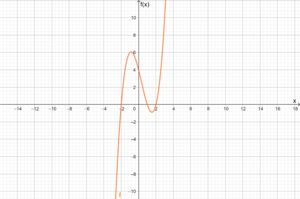
4. Ja, da jedem Argument genau ein Wert zugeordnet wird, handelt es sich um den Graphen einer Funktion (Funktionsgraph).

Siehe auch

• Vorlage:Show-Hide (in englischer Sprache)

ppvafpsdn20

Quiz

Kreuze die zutreffende

1. A Jede Funktion hat mindestens so viele verschiedene Funktionswerte wie Argumente.
2. D Es gibt Funktionen, die genauso viele Argumente wie Funktionswerte besitzen.
3. n
4. C Jede Funktion ordnet jedem Funktionswert genau ein Argument zu.
5. B Jede Funktion ordnet jedem Argument genau einen Funktionswert zu.
6. n
7. E Jede Funktion besitzt genauso viele Argumente wie Funktionswerte.

prüfen!

neu starten