Signifikanztest für binomialverteilte Zufallsgrößen/Aufbau und Durchführung eines Signifikanztests: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
1. Schritt: Wahl der Nullhypothese <math>H_0</math> und der Gegenhypothese <br> | 1. Schritt: Wahl der Nullhypothese <math>H_0</math> und der Gegenhypothese <math>H_1</math> <br> | ||
Die Nullhypothese <math>H_0</math> beschreibt die Wahrscheinlichkeit <math>p_0</math>, die bisher für die Grundgesamtheit galt: <math>H_0:p=p_0</math>. Durch bestimmte Einflüsse wird vermutet, dass <math>p_0</math> gesunken bzw. gestiegen ist. Diese Vermutung wird durch die Gegenhypothese <math>H_1</math> ausgedrückt.<math>H_1</math> lautet also entweder <math>H_1:p<p_0</math> oder <math>H_1:p>p_0</math>. Das Ziel des Signifikanztests ist es, die Nullhypothese <math>H_0</math> zu verwerfen. Kann die Nullhypothese verworfen werden, so ist mit einer großen statistischen Sicherheit gezeigt, dass die Gegenhypothese <math>H_1</math> gilt. | Die Nullhypothese <math>H_0</math> beschreibt die Wahrscheinlichkeit <math>p_0</math>, die bisher für die Grundgesamtheit galt: <math>H_0:p=p_0</math>. Durch bestimmte Einflüsse wird vermutet, dass <math>p_0</math> gesunken bzw. gestiegen ist. Diese Vermutung wird durch die Gegenhypothese <math>H_1</math> ausgedrückt.<math>H_1</math> lautet also entweder <math>H_1:p<p_0</math> oder <math>H_1:p>p_0</math>. Das Ziel des Signifikanztests ist es, die Nullhypothese <math>H_0</math> zu verwerfen. Kann die Nullhypothese verworfen werden, so ist mit einer großen statistischen Sicherheit gezeigt, dass die Gegenhypothese <math>H_1</math> gilt. | ||
</div> | </div> | ||
| Zeile 26: | Zeile 26: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn <math>H_0</math> stimmt<br> | 3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn <math>H_0</math> stimmt<br> | ||
Die Zufallsvariable X der zugrundeliegenden Verteilung | Die Zufallsvariable X der zugrundeliegenden Verteilung muss definiert werden. Zudem muss noch die konkrete Verteilung angegeben werden (die Verteilung deiner Skizze), also die Verteilung der Nullhypothese <math>H_0</math>.<br><br> | ||
</div> | </div> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
4. Schritt: Entscheidungsregel angeben <br> | 4. Schritt: Entscheidungsregel angeben <br> | ||
In diesem Schritt wird der Verwerfungsbereich für die Zufallsvariable X angegeben. Der Verwerfungsbereich ist der Bereich, der in deiner Skizze markiert ist. Es ist also der Bereich, in dem man aussagen kann, dass mit einer großen statistischen Sicherheit <math>p_0</math> gesunken bzw. gestiegen ist | In diesem Schritt wird der Verwerfungsbereich für die Zufallsvariable X angegeben. Der Verwerfungsbereich ist der Bereich, der in deiner Skizze markiert ist. Es ist also der Bereich, in dem man aussagen kann, dass mit einer großen statistischen Sicherheit <math>p_0</math> gesunken bzw. gestiegen ist. In diesem Bereich wird also die Nullhypothese <math>H_0</math> verworfen. Der Verwerfungsbereich wird durch den kritischer Wert k festgelegt, bis zu diesem Wert k (linksseitiger Test) beziehungsweise ab diesem Wert k (rechtsseitiger Test) wird die Nullhypothese <math>H_0</math> verworfen. <br> | ||
Hinweis zur Ermittlung des kritischen Wertes k: | Hinweis zur Ermittlung des kritischen Wertes k: | ||
| Zeile 40: | Zeile 40: | ||
Rechtsseitiger Test:<br> | Rechtsseitiger Test:<br> | ||
<math> | <math>P(X\leq k-1)\geq1-\alpha</math><br> | ||
Zur Auswertung dieser Formel erstellt man eine Tabelle mit den kumulierten Wahrscheinlichkeiten der Binomialverteilung. Man liest den Wert k ab, bei dem die kumulierte Wahrscheinlichkeit zum ersten Mal größer gleich <math>1-\alpha</math> ist. Dieser Wert muss anschließend noch plus 1 gerechnet werden. Ab diesem Wert wird die Nullhyothese verworfen. | |||
</div> | </div> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Liegt das Stichprobenergebnis im Verwerfungsbereich, so kann die Nullhypothese <math>H_0</math> zugunsten der Gegenhypothese <math>H_1</math> verworfen werden. Die Irrtumswahrscheinlichkeit für diese Schlussfolgerung ist | Liegt das Stichprobenergebnis im Verwerfungsbereich, so kann die Nullhypothese <math>H_0</math> zugunsten der Gegenhypothese <math>H_1</math> verworfen werden. Die Irrtumswahrscheinlichkeit für diese Schlussfolgerung ist gleich dem festgelegten Signifikanzniveau <math>\alpha</math>. Liegt das Stichprobenergebnis nicht im Verwerfungsbereich, so kann die Nullhypothese nicht zugunsten von <math>H_1</math> verworfen werden. Es ist keine statistische Aussage zur wahren Verteilung möglich. <br><br> | ||
</div> | </div> | ||
| Zeile 54: | Zeile 53: | ||
Eine Partei sieht den Klimawandel nicht als Bedrohung an. Diese Partei hat ihre Argumente gegen die Bedrohung des Klimawandels im Jahr 2019 in vielen Debatten ausführlich erläutert. Die Partei interessiert sich, ob daher der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019, wo der Wert bei 71% lag, gesunken ist. Sie beschließt in einer Umfrage zufällig 1000 Menschen zu befragen und das Ergebnis anschließend mit einem Signifikanztest zu beurteilen. Das Signifikanzniveau <math>\alpha</math> legen sie auf 5% fest. | Eine Partei sieht den Klimawandel nicht als Bedrohung an. Diese Partei hat ihre Argumente gegen die Bedrohung des Klimawandels im Jahr 2019 in vielen Debatten ausführlich erläutert. Die Partei interessiert sich, ob daher der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019, wo der Wert bei 71% lag, gesunken ist. Sie beschließt in einer Umfrage zufällig 1000 Menschen zu befragen und das Ergebnis anschließend mit einem Signifikanztest zu beurteilen. Das Signifikanzniveau <math>\alpha</math> legen sie auf 5% fest. | ||
Führe einen passenden Signifikanztest durch.<br><br> | Führe einen passenden Signifikanztest durch.<br><br> | ||
<br><br> | <br><br> | ||
Vorüberlegung: Skizze zeichnen | Vorüberlegung: Skizze zeichnen | ||
| Zeile 118: | Zeile 116: | ||
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus <math>\alpha</math> | 2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus <math>\alpha</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
n= | n=1000 und <math>\alpha=5%</math> | ||
}} | }} | ||
| Zeile 128: | Zeile 126: | ||
4. Schritt: Entscheidungsregel angeben | 4. Schritt: Entscheidungsregel angeben | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= Lies dir oben im Kasten zu dem 4. Schritt die Informationen zum rechtseitigen Test durch. | ||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math>P(X\ | <math>P(X\leq k-1)\geq0,95</math><br>[[Datei:Unbenannt.png|mini]] Man liest also den Wert ab, bei dem die kumulierte Wahrscheinlichkeit zum ersten mal größer gleich 0,95 ist. In diesem Fall 733. Da dies der kritische Wert minus 1 ist, rechnet man noch plus 1 und erhält somit den kritischen Wert, in dem Fall 734. Es ergibt sich folgender Verwerfungsbereich: {734,...1000}. | ||
}} | }} | ||
In der Umfrage kommt raus, dass 748 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie können die Schüler*innen dieses Ergebnis interpretieren? | In der Umfrage kommt raus, dass 748 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie können die Schüler*innen dieses Ergebnis interpretieren? | ||
| Zeile 142: | Zeile 141: | ||
'''Zweiseitiger Signifikanztest: '''<br> | '''Zweiseitiger Signifikanztest: '''<br> | ||
Neben dem links- und rechtsseitigen Test gibt es auch noch den zweiseitigen Test. Bei dieser Art des Tests will der Auftragsgeber zeigen, dass eine Aussage falsch ist. Der Auftragsgeber weiß allerdings noch nicht, ob der tatsächliche Wert nach links oder rechts abweicht. Die Durchführung des Tests erfolgt sehr ähnlich zum links- und rechtsseitigen Test, aber mit folgenden Unterschieden:<br> | Neben dem links- und rechtsseitigen Test gibt es auch noch den zweiseitigen Test. Bei dieser Art des Tests will der Auftragsgeber zeigen, dass eine Aussage falsch ist. Der Auftragsgeber weiß allerdings noch nicht, ob der tatsächliche Wert nach links oder rechts abweicht. Die Durchführung des Tests erfolgt sehr ähnlich zum links- und rechtsseitigen Test, aber mit folgenden Unterschieden:<br> | ||
1.) Die Gegenhypothese <math>H_1</math> ist die Gegenaussage zur Nullhypothese <math>H_1:p\neq p_0</math>.<br> | 1.) Die Gegenhypothese <math>H_1</math> ist die Gegenaussage zur Nullhypothese: <math>H_1:p\neq p_0</math>.<br> | ||
2.) Das Signifikanzniveau <math>\alpha</math> wird halbiert und auf beide Ränder der Binomialverteilung aufgeteilt. Der Verwerfungsbereich besteht somit aus der Vereinigung von zwei Intervallen.<br><br><br> | 2.) Das Signifikanzniveau <math>\alpha</math> wird halbiert und auf beide Ränder der Binomialverteilung aufgeteilt. Der Verwerfungsbereich besteht somit aus der Vereinigung von zwei Intervallen.<br><br><br> | ||
Führe in der nächsten Übung einen zweiseitigen Signifikanztest durch. | Führe in der nächsten Übung einen zweiseitigen Signifikanztest durch. | ||
Aktuelle Version vom 9. März 2020, 13:30 Uhr
Die Grundidee vom Signifikanztest hast du bereits verstanden. Auf dieser Seite lernst du nun den Aufbau und die Begrifflichkeiten eines Signifikanztests kennen.
Ein Signifikanztest besteht aus vier Schritten.
Im Folgenden werden die einzelnen Schritte ausführlich beschrieben. Lies dir die Beschreibungen aufmerksam durch, im Anschluss gibt es zwei Übungen, in denen du eigenständig einen Signifikanztest durchführst.
Vorüberlegung:
Skizziere die Binomialverteilung für die Stichprobe mit der bisher geltenden Wahrscheinlichkeit . Kläre die Frage, ob durch bestimmte Einflüsse vermutet wird, dass die bisherige Wahrscheinlichkeit gesunken bzw. gestiegen ist. Falls die Vermutung vorliegt, dass die Wahrscheinlichkeit gesunken ist, liegt ein linksseitiger Test vor, so markiere den linken Rand der Binomialverteilung. Liegt der Verdacht vor, dass die Wahrscheinlichkeit gestiegen ist, so handelt es sich um einen rechtsseitigen Test und es ist der rechte Rand der Verteilung zu markieren.
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
Die Nullhypothese beschreibt die Wahrscheinlichkeit , die bisher für die Grundgesamtheit galt: . Durch bestimmte Einflüsse wird vermutet, dass gesunken bzw. gestiegen ist. Diese Vermutung wird durch die Gegenhypothese ausgedrückt. lautet also entweder oder . Das Ziel des Signifikanztests ist es, die Nullhypothese zu verwerfen. Kann die Nullhypothese verworfen werden, so ist mit einer großen statistischen Sicherheit gezeigt, dass die Gegenhypothese gilt.
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
Der Stichprobenumfang n und das Signifikanzniveau sind meistens in der Aufgabenstellung angegeben. Diese Größen musst du also einfach nur aus dem Aufgabentext herausschreiben. Das Signifikanzniveau legt die Irrtumswahrscheinlichkeit fest, eine Nullhypothese fälschlicherweise zu verwerfen. Die Höhe des Signifikanzniveaus legt der Auftragsgeber vor der Durchführung des Tests fest. Ein üblicher Wert ist Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \alpha=5%}
. Manchmal wird aber auch ein strenges Niveau von Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \alpha=1%}
gewählt.
3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn stimmt
Die Zufallsvariable X der zugrundeliegenden Verteilung muss definiert werden. Zudem muss noch die konkrete Verteilung angegeben werden (die Verteilung deiner Skizze), also die Verteilung der Nullhypothese .
4. Schritt: Entscheidungsregel angeben
In diesem Schritt wird der Verwerfungsbereich für die Zufallsvariable X angegeben. Der Verwerfungsbereich ist der Bereich, der in deiner Skizze markiert ist. Es ist also der Bereich, in dem man aussagen kann, dass mit einer großen statistischen Sicherheit gesunken bzw. gestiegen ist. In diesem Bereich wird also die Nullhypothese verworfen. Der Verwerfungsbereich wird durch den kritischer Wert k festgelegt, bis zu diesem Wert k (linksseitiger Test) beziehungsweise ab diesem Wert k (rechtsseitiger Test) wird die Nullhypothese verworfen.
Hinweis zur Ermittlung des kritischen Wertes k:
Linksseitiger Test:
Zur Bestimmung des kritischen Wertes k erstellt man eine Tabelle mit den kumulierten Wahrscheinlichkeiten der Binomialverteilung. Der kritische k-Wert ist der Wert, bei dem die kumulierte Wahrscheinlichkeit gerade noch kleiner als das Signifikanzniveau ist. Bis zu diesem Wert wird die Nullhypothese verworfen.
Rechtsseitiger Test:
Zur Auswertung dieser Formel erstellt man eine Tabelle mit den kumulierten Wahrscheinlichkeiten der Binomialverteilung. Man liest den Wert k ab, bei dem die kumulierte Wahrscheinlichkeit zum ersten Mal größer gleich ist. Dieser Wert muss anschließend noch plus 1 gerechnet werden. Ab diesem Wert wird die Nullhyothese verworfen.
Liegt das Stichprobenergebnis im Verwerfungsbereich, so kann die Nullhypothese zugunsten der Gegenhypothese verworfen werden. Die Irrtumswahrscheinlichkeit für diese Schlussfolgerung ist gleich dem festgelegten Signifikanzniveau . Liegt das Stichprobenergebnis nicht im Verwerfungsbereich, so kann die Nullhypothese nicht zugunsten von verworfen werden. Es ist keine statistische Aussage zur wahren Verteilung möglich.
Versuche jetzt im Folgenden, eigenständig einen Signifikanztest durchzuführen! Hast du Probleme bei einzelnen Schritten, so lies dir die Informationen oben nochmal genau durch!
Eine Partei sieht den Klimawandel nicht als Bedrohung an. Diese Partei hat ihre Argumente gegen die Bedrohung des Klimawandels im Jahr 2019 in vielen Debatten ausführlich erläutert. Die Partei interessiert sich, ob daher der Anteil der Menschen, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019, wo der Wert bei 71% lag, gesunken ist. Sie beschließt in einer Umfrage zufällig 1000 Menschen zu befragen und das Ergebnis anschließend mit einem Signifikanztest zu beurteilen. Das Signifikanzniveau legen sie auf 5% fest.
Führe einen passenden Signifikanztest durch.
Vorüberlegung: Skizze zeichnen
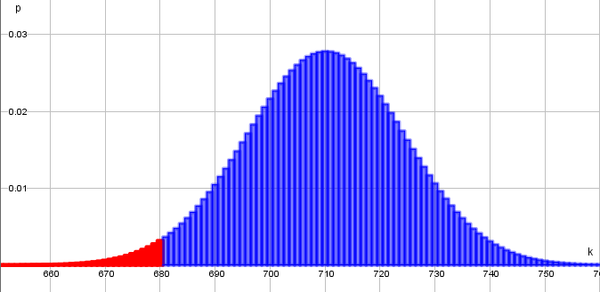
Markiere in der Skizze den Bereich, in dem die Partei mit einer großen statistischen Sicherheit zeigen kann, dass der Anteil gesunken ist.
Um welche Art von Test handelt es sich?
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvaraible X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
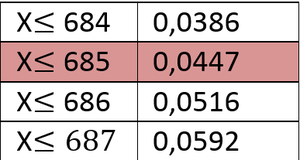
Durch Ablesen der Tabelle erhalten wir den kritischen Wert 685. Bis zu diesem Wert wird die Nullhypothese abgelehnt. Es ergibt sich folgender Verwerfungsbereich:{0, ...685}
In der Umfrage kommt raus, dass sich 750 Menschen von den 1000 Befragten durch den Klimawandel bedroht fühlen. Was kann die Partei mit diesem Ergebnis aussagen?
Eine Umweltgruppe will raus finden, ob durch die hohe Öffentlichkeit des Klimawandel-Themas 2019 - unter anderem auch ausgelöst durch die Fridays For Future Demos - der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019, wo der Wert bei 71% lag, gestiegen ist. Sie beschließt, in einer Umfrage zufällig 1000 Menschen zu befragen und das Ergebnis anschließend mit einem Signifikanztest zu beurteilen. Das Signifikanzniveau legen sie auf 5% fest.
Führe einen passenden Signifikanztest durch.
Vorüberlegung : Skizze zeichnen
Um welche Art von Test handelt es sich?
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
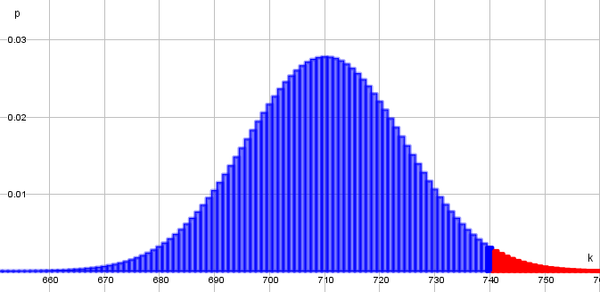
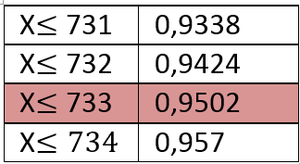
Man liest also den Wert ab, bei dem die kumulierte Wahrscheinlichkeit zum ersten mal größer gleich 0,95 ist. In diesem Fall 733. Da dies der kritische Wert minus 1 ist, rechnet man noch plus 1 und erhält somit den kritischen Wert, in dem Fall 734. Es ergibt sich folgender Verwerfungsbereich: {734,...1000}.
In der Umfrage kommt raus, dass 748 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie können die Schüler*innen dieses Ergebnis interpretieren?
Zweiseitiger Signifikanztest:
Neben dem links- und rechtsseitigen Test gibt es auch noch den zweiseitigen Test. Bei dieser Art des Tests will der Auftragsgeber zeigen, dass eine Aussage falsch ist. Der Auftragsgeber weiß allerdings noch nicht, ob der tatsächliche Wert nach links oder rechts abweicht. Die Durchführung des Tests erfolgt sehr ähnlich zum links- und rechtsseitigen Test, aber mit folgenden Unterschieden:
1.) Die Gegenhypothese ist die Gegenaussage zur Nullhypothese: .
2.) Das Signifikanzniveau wird halbiert und auf beide Ränder der Binomialverteilung aufgeteilt. Der Verwerfungsbereich besteht somit aus der Vereinigung von zwei Intervallen.
Führe in der nächsten Übung einen zweiseitigen Signifikanztest durch.
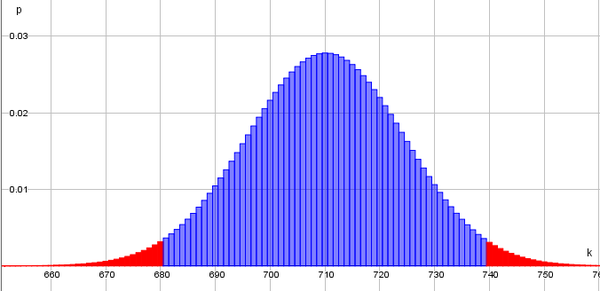
2019 wurde veröffentlicht, dass sich 71% der Menschen in Deutschland durch den Klimawandel bedroht fühlen. Journalisten einer Zeitung hinterfragen diesen Wert. Sie wollen also diesen Wert mit einem zweiseitigen Signifikanztest überprüfen. Ihnen geht es hierbei nur um den Wahrheitsgehalt, aber nicht ob der Wert größer oder kleiner ist. Sie beschließen zufällig 1000 Menschen zu befragen. Das Signifikanzniveau legen sie auf 10% fest.
Führe den zweiseitigen Signifikanztest durch.
Vorüberlegung : Skizze zeichnen
Um welche Art von Test handelt es sich?
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
1.) Aus Ablesen in der Tabelle erhält man den kritischen Wert 685.
2.) Aus Ablesen in der Tabelle erhält man den kritischen Wert 734.
In der Umfrage kommt raus, dass sich 745 Menschen von den 1000 Befragten durch den Klimawandel bedroht fühlen. Wie können die Journalisten dieses Ergebnis interpretieren?