Signifikanztest für binomialverteilte Zufallsgrößen/Aufbau und Durchführung eines Signifikanztests: Unterschied zwischen den Versionen
(Seite wurde verschoben) Markierung: Quelltext-Bearbeitung 2017 |
(Skizze zweiseitiger Test wurde hinzugefügt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 127: | Zeile 127: | ||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
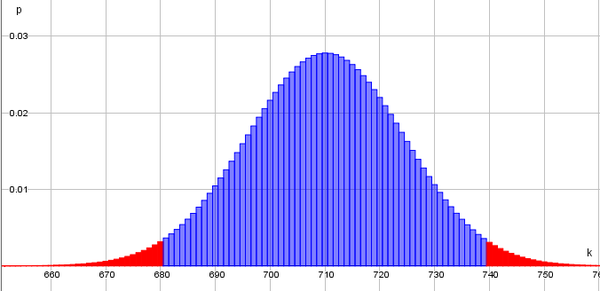
[[Datei:Zweiseitigertest.png|600px]]<br> | |||
Da der Verwerfungsbereich an beiden Rändern der Binomialverteilung liegt, handelt es sich um einen zweiseitigen Test. | Da der Verwerfungsbereich an beiden Rändern der Binomialverteilung liegt, handelt es sich um einen zweiseitigen Test. | ||
}} | }} | ||
Version vom 15. Dezember 2019, 09:51 Uhr
Super! Jetzt hast du schon die Grundidee vom Testen verstanden. Auf dieser Seite lernst du jetzt aus welchen Schritten ein Signifikanztest genau besteht. Danach führst du eigenständig Signifikanztests durch.
Ein Signifikanztest besteht aus vier Schritten. In der folgenden Abbilung findest du eine Übersicht der vier Durchführungsschritte.
Im Folgenden werde die einzelnen Schritte genauer beschrieben. Lies dir die Informationen aufmerksam durch.
Vorüberlegungen:
Skizziere die Binomialverteilung für die bisher geltende bzw. angenommene Wahrscheinlichkeit. Markiere in der Skizze grob den Annahme- und Verwerfungsbereich. Der Verwerfungsbereich ist der Bereich, indm der Auftraggeber des Tests hofft mit dem Stichprobenergebnis zu landen.
Liegt der Verwerfungsbereich am linken Rand der Binomialverteilungt, so handelt es sich um einen linksseitigen Test
Liegt der Verwerfungsbereich am rechten Rand der Binomialverteilung, so liegt ein rechtsseitiger Test vor.
Schätze zudem intuitiv die Intervalle des Annahmebereichs und des Verwerfungsbereichs. So kannst du später dein Ergebnis überprüfen.
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
Vor Durchführung des Tests gibt es immer eine angenommene bzw. geltende Wahrscheinlichkeit, die für die Grundgesamtheit gilt bzw.galt. Das Ziel des Tests ist es zu zeigen, dass die tatsächliche Wahrscheinlichkeit größer bzw. kleiner geworden ist. Für den Signifikanztest werden dafür zwei Hypothesen formuliert: Die Nullhypothese und die Gegenhypothese . Es ist einfacher zuerst die Gegenhypothese zu formuliern. Die Gegenhypothese entspricht immer den Interessen des Auftragsgebers. Also überlege dir, ob der Auftraggeber durch den Test zeigen möchte, dass die tatäschliche Wahrscheinlichkeit kleiner (p< als bisher geltende Wahrscheinlichkeit) bzw. größer (p> als bisher geltende Wahrscheinlichkeit) durch bestimmte Einflüsse geworden ist. Wähle dies als Gegenhypothese . Die entsprechende Gegenaussage inklusive Grenzfall ist dann die zugehörige Nullhypothese .
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
Der Stichprobenumfang n und das Signifikanzniveau sind meistens in der Aufgabenstellung angegeben. Diese Größen musst du also einfach nur aus dem Aufgabentext rausschreiben
3. Schritt: Definition der Zufallsvariable X und angeben der Verteilung wenn stimmt
Die Zufallsvariable X muss so gewählt werden, dass sie von den zu überprüfenden Hypothesen abhängt. Zudem muss noch die Verteilung angegeben werden, unter der Voraussetzung das der Grenzfall von stimmt. In diesem Lernpfad und in den Schul- und Abituraufgaben ist die Zufallsvariable X immer binomialverteilt. Dennoch ist es wichtig, dass du es notierst, sonst musst du mit Punktabzug rechnen.
4. Schritt: Entscheidungsregel angeben
In diesem Schritt werden die Intervalle für den Annahme- und Verwerfungsbereich angegeben. Dafür wird ein kritischer Wert ermittelt. Ab diesem Wert liegen signifikante Abweichung (nach links oder rechts) zu der in definierten Nullhypothese vor. Ab diesem Wert wird die Nullhypothese verworfen.
Nachdem der Signifikanztest durchgeführt wurde, wird eine Stichprobe erhoben. Liegt das Ergegnis der Stichprobe im Annahmebereich, so ist keine Aussage möglich. Liegt dagegen das Stichporbenergebnis im Verwerfungsbereich, so kann man unter der festgelegten Irrtumswahrscheinlichkeit (=Signifikanzniveau ) sagen, dass die Gegenhypothese gilt.
Versuche jetzt im Folgenden, eigenständig Signifikanztests durchzuführen.
Eine Patrei sieht den Klimawandel nicht als Bedrohung an. Ihre Argumente dafür, hat sie im laufe des Jahres 2019, stark öffentlich erläutert. Sie will daher am liebsten kein Klimaschutzprogramm in ihr Wahlprogramm aufnehmen. Aber auch die Patrei hat die Information, dass 2019, 71% der Deutschen sich durch den Klimawandel bedroht gefühlt haben. Da dies kein geringer Anteil ist, beschließen sie einen Signifikanztest durchzuführen. Falls durch den Signifikanztest sich zeigen lässt, dass der Anteil im Vergleich zu 2019 gesunken ist, wollen sie kein Klimaschutz in ihr Wahlprogramm aufnehmen. Sie beschließen 1000 Menschen zu befragen und legen das Signifikanzniveau auf 5% fest.
Führe einen passenden Signifikanztest durch.
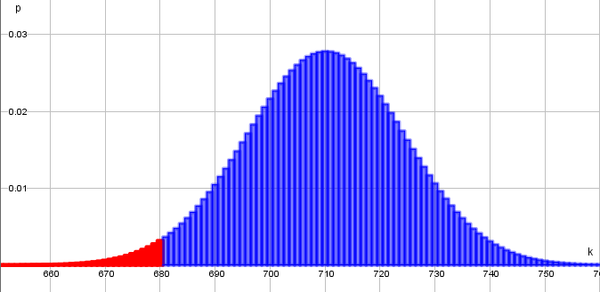
Vorüberlegung : Skizze zeichnen
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvaraible X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
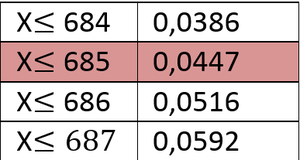
Aus Ablesen der Tabelle erhalten wir den kritischen Wert 685. Es ergeben sich folgende Annahme- und Verwerfungsbereich: Annahmebereich:{686, ..., 1000}, Verwerfungsbereich:{0, ...685}
In der Umfrage kommt raus, dass sich 750 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie kann die Partei dieses Ergebnis interpretieren?
Eine Fridays For Future Gruppe will raus finden, ob der Anteil der Menschen, die sich durch den Klimawandel bedroht fühlen, gestiegen ist. Anfang des Jahres 2019 wurde veröffentlicht, dass sich 71% der Menschen in Deutschland durch den Klimwandel bedroht fühlen. Im Jahr 2019 ist das Thema des Klimwandels vermehrt, unteranderem auch wegen der Fridays For Future Demos, in den Medien gewesen. Die Schüler*innen hoffen deswegen darauf, dass der Anteil gestiegen ist. Es werden 1000 Menschen in Deutschland befragt und das Signifikanzniveau wird auf 5% festgelegt. Führe einen passenden Signifkanztest durch.
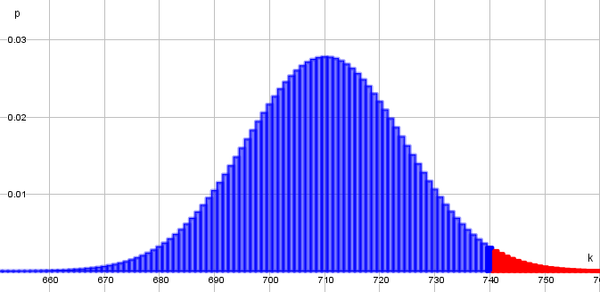
Vorüberlegung : Skizze zeichnen
Schätze mit Hilfe der Skizze den Annahme- und Verwerfungsbereich.
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvaraible X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
Erinnere dich daran wie du Mindestwahrscheinlichkeiten berechnen kannst.
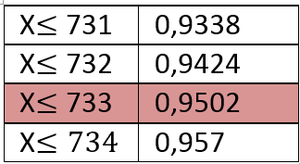
Mindestwahrscheinlichkeiten werden über die Gegenwahrscheinlichkeit berechnet, es folgt . Durch Umformen der Gleichung erhält man .Man liest also den Wert ab, bei dem die kumulierte Wahrscheinlichkeit zum ersten mal größer gleich 0,95 ist. In diesem Fall 733. Da dies der kritische Wert minus 1 ist, rechnet man noch plus 1 und erhält somit den kritischen Wert. Es ergeben sich folgende Annahme- und Verwerfungsbereiche: Annahmebereich {0,...,733}, Verwerfungsbereich {734,...1000}
In der Umfrage kommt raus, dass sich 748 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie können die Schüler*innen dieses Ergebnis interpretieren?
Neben dem links- und rechtsseitigen Test gibt es auch noch den zweiseitigen Test. Bei dieser Art des Tests interessiert sich der/die Auftragsgeber*in für signifikanten Abweichungen nach links und rechts. Die Durchfühung des Tests erfolgt analog zum links- und rechtsseitigen Test, mit nur minimalen Unterschieden.
1.) Die Nullhypothese wird nicht als Intervall formuliert, sondern als Punkt( bisher geltende Wahrscheinlichkeit). Die Gegenhypothese ist entsprechend die Gegenaussage ( bisher geltende Wahrscheinlichkeit).
2. Das Signifikanzniveau wird halbiert und auf beide Ränder der Binomialverteilung aufgeteilt . Der Verwerfungsbereich besteht somit aus der Vereinignung von zwei Intervallen.
Führe in der nächsten Übung einen zweiseitigen Signifikanztest durch.
Journalisten für eine Zeitung wollen einen Bericht über den Klimawandel veröffentlichen. Unteranderem wollen sie auch berichten, ob der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung ansehen im Vergleich zu 2019 (71%) gesunken bzw. gestiegen ist. Sie wollen daher einen zweiseitigen Signifikanztest durchführen. Dafür wollen sie 1000 Menschen in Deutschland befragen und legen das Signifikanzniveau auf 5% fest.
Führe den Signifkanztest durch.
Vorüberlegung : Skizze zeichnen
Schätze mit Hilfe der Skizze den Annahme- und Verwerfungsbereich.
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt: Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt: Definition der Zufallsvaraible X und angeben der Verteilung wenn stimmt
X ist die Anzahl der 1000 Befragten, die den Klimawandel als Bedrohung ansehen.
4. Schritt: Entscheidungsregel angeben
1.) Aus Ablesen in der Tabelle erhält man den kritischen Wert 681.
2.) Aus Ablesen in der Tabelle erhält man den kritischen Wert 739.
In der Umfrage kommt raus, dass sich 745 Menschen von den 1000 Befragten sich durch den Klimawandel bedroht fühlen. Wie können die Journalisten dieses Ergebnis interpretieren?
Super gemacht! Versuche jetzt in der letzten Übung nochmal zu überpürfen, ob du die Reihenfolge der Schritte auch schon auswendig kannst. Zur Erinnerung: Du musst alle Schritte bei einem Signifkanztest notieren, um die volle Punktzahl in Klausuren zu erhalten! Versuche nicht hoch zu scrollen;)
Bringe die Schritte des Signifikanztests in die richtige Reihenfolge!
Vorüberlegungen:Skizze zeichnen
1. Schritt: Wahl der Nullhypothese und der Gegenhypothese
2. Schritt:Festlegen des Stichprobenumfangs n und des Signifikanzniveaus
3. Schritt:Definition der Zufallsvariable X und der Verteilung wenn stimmt.
4. Schritt:Entscheidungsregel angeben