Benutzer:Uschuetzenmeister/Test Uwe/Lernmodule Maria: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
 
(11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Kurzinfo|DSB/IQB|DSB-1|M-digital|Quiz}}
<div>
<div>
[http://www.iqb.hu-berlin.de/bista/aufbsp/vera8_2009/Mathematik_Testheft_A.pdf '''Testheft A zum Download''']
[http://www.iqb.hu-berlin.de/bista/aufbsp/vera8_2009/Mathematik_Testheft_A.pdf '''Testheft A zum Download''']
Zeile 15: Zeile 13:
<big>'''Aufgabe 2: Stadion '''</big>
<big>'''Aufgabe 2: Stadion '''</big>


Ein Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze <br>und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €.
Ein kleines Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze.<br>und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €.


Wie viel Geld nimmt der Verein bei einem vollen Stadion ein?
Wie viel Geld nimmt der Verein bei einem vollen Stadion ein?
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:'''120 700 Euro'''
'''120 700 Euro'''
:*5300 Sitzplätze · 14 Euro = 74200 Euro
*5300 Sitzplätze · 14 Euro = 74200 Euro
:*9300 Stehplätze · 5 Euro = 46500 Euro
*9300 Stehplätze · 5 Euro = 46500 Euro
:*74200 + 46500 Euro = 120700 Euro
*74200 + 46500 Euro = 120700 Euro
}}
}}
</div>
</div>
Zeile 57: Zeile 55:
Erkläre, wie Petra zu dieser Aussage kommt.
Erkläre, wie Petra zu dieser Aussage kommt.
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:*1 Euro - 73 Cent = 27 Cent, das entspricht ca. 25% bzw. 1/4.
*1 Euro - 73 Cent = 27 Cent, das entspricht ca. 25% bzw. 1/4.
:*73 Cent pro Euro bedeutet 73% Steuern, also etwa 3/4. Also etwas 1/4 ohne Steuern.
*73 Cent pro Euro bedeutet 73% Steuern, also etwa 3/4. Also etwas 1/4 ohne Steuern.
:*74200 + 46500 Euro = 120700 Euro
*74200 + 46500 Euro = 120700 Euro
}}
}}
</div>
</div>
Zeile 83: Zeile 81:
Erkläre, warum das so ist, ohne das Ergebnis auszurechnen.
Erkläre, warum das so ist, ohne das Ergebnis auszurechnen.
<div>
<div>
:{{Lösung versteckt|1=zum Beispiel:
{{Lösung versteckt|1=zum Beispiel:
:* 248, 146, 320 sind gerade Zahlen. werden diese Zahlen addiert, dann ist auch das Ergebnis eine gerade Zahl''
* 248, 146, 320 sind gerade Zahlen. werden diese Zahlen addiert, dann ist auch das Ergebnis eine gerade Zahl''
:* In den Zahlen sind nur gerade Zahlen.''
* In den Zahlen sind nur gerade Zahlen.''
}}
}}
</div>
</div>
Zeile 105: Zeile 103:


<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:#49
#49
:#275
#275
}}
}}
</div>
</div>
Zeile 117: Zeile 115:


<div>
<div>
:{{Lösung versteckt|
{{Lösung versteckt|
:''"Obere Zahl mal 2 und dann plus 2"'' oder ''"Obere Zahl plus 1 und dann mal 2"''
''"Obere Zahl mal 2 und dann plus 2"'' oder ''"Obere Zahl plus 1 und dann mal 2"''
}}
}}
</div>
</div>
Zeile 131: Zeile 129:


<div>
<div>
:{{Lösung versteckt|
{{Lösung versteckt|
:20 mal
20 mal
}}
}}
</div>
</div>
Zeile 139: Zeile 137:


<div>
<div>
:{{Lösung versteckt|
{{Lösung versteckt|
:189 Ziffern
189 Ziffern
}}
}}
</div>
</div>
Zeile 173: Zeile 171:


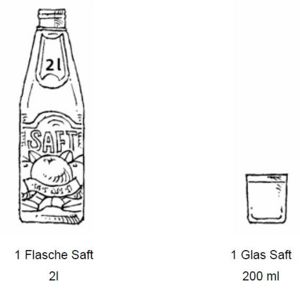
<div>
<div>
:{{Lösung versteckt|
{{Lösung versteckt|
:Die Flasche reicht für '''10''' Gläser Saft.
Die Flasche reicht für '''10''' Gläser Saft.
}}
}}
</div>
</div>
Zeile 186: Zeile 184:


<div>
<div>
:{{Lösung versteckt|
{{Lösung versteckt|
:z.B.: ''Das Dreieck ABC ist gleichschenklig und hat einen Innenwinkel von 60<sup>0</sup>. Folglich müsste dieses Dreieck gleichseitig sein. Daher müssten alle Seiten entweder 39,5 cm oder 45 cm lang sein.''
z.B.: ''Das Dreieck ABC ist gleichschenklig und hat einen Innenwinkel von 60<sup>0</sup>. Folglich müsste dieses Dreieck gleichseitig sein. Daher müssten alle Seiten entweder 39,5 cm oder 45 cm lang sein.''
}}
}}
</div>
</div>
Zeile 200: Zeile 198:
27 € 50 Cent = ..... '''Euro'''
27 € 50 Cent = ..... '''Euro'''
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:27 € 50 Cent =''' 27,50 Euro'''
27 € 50 Cent =''' 27,50 Euro'''
}}
}}
</div>
</div>
Zeile 209: Zeile 207:
1 € 1 Cent = ..... '''Cent'''
1 € 1 Cent = ..... '''Cent'''
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:1 € 1 Cent = '''101 Cent'''
1 € 1 Cent = '''101 Cent'''
}}
}}
</div>
</div>
Zeile 226: Zeile 224:
..... s = 3 min 28 s
..... s = 3 min 28 s
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:'''208 s''' = 3 min 28 s
'''208 s''' = 3 min 28 s
}}
}}
</div>
</div>
Zeile 235: Zeile 233:
136 s = ..... min ..... s
136 s = ..... min ..... s
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:136 s = '''2''' min '''16''' s
136 s = '''2''' min '''16''' s
}}
}}
</div>
</div>
Zeile 243: Zeile 241:
..... s = 8 min 20 s
..... s = 8 min 20 s
<div>
<div>
:{{Lösung versteckt|1=
{{Lösung versteckt|1=
:'''500''' s = 8 min 20 s
'''500''' s = 8 min 20 s
}}
}}
</div>
</div>
Zeile 268: Zeile 266:
<div class="multiplechoice-quiz">
<div class="multiplechoice-quiz">
<big>'''Aufgabe 16: Winkel im Dreieck'''</big>
<big>'''Aufgabe 16: Winkel im Dreieck'''</big>
 
   
In einem gleichschenkligen Dreieck ist der Winkel <math>\gamma</math> an der Spitze dreimal so groß wie ein Basiswinkel <math>\alpha</math>.
 
Wie groß sind die Winkel dieses Dreiecks? Kreuze die richtige Antwort an.
 
(!<math>\alpha=30^0; \gamma = 90^0</math>) (!<math>\alpha=30^0; \gamma = 90^0</math>)  (<math>\alpha=36^0; \gamma = 108^0</math>)  (!<math>\alpha=22,5^0; \gamma = 135^0</math>)
</div>
</div>

Aktuelle Version vom 26. Oktober 2019, 18:36 Uhr

Aufgabe 1: Umkehraufgabe

Zu welcher Zahl muss man 6345 addieren, um 8567 zu erhalten? (!2023) (2222) (!1987) (!14912)

Aufgabe 2: Stadion

Ein kleines Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze.
und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €.

Wie viel Geld nimmt der Verein bei einem vollen Stadion ein?

120 700 Euro

  • 5300 Sitzplätze · 14 Euro = 74200 Euro
  • 9300 Stehplätze · 5 Euro = 46500 Euro
  • 74200 + 46500 Euro = 120700 Euro

Aufgabe 3: Basketball

Bei einem Basketball-Turnier einer Hauptschule nehmen vier achte Klassen, fünf neunte Klassen und zwei zehnte Klassen teil.

Die Klassen werden in der Vorrunde in zwei Gruppen (Gruppe A und Gruppe B) aufgeteilt. Jede Klasse einer Gruppe spielt gegen jede andere Klasse dieser Gruppe. Fünf Klassen sind in der Gruppe A. Wie viele Spiele finden in der Vorrunde in Gruppe A statt? Kreuze an:

(!5 Spiele) (10 Spiele) (!15 Spiele) (!25 Spiele)

Aufgabe 4: Zapfsäule 1

AufgabeA4 Zapfsäule.jpg

Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. Wie viel erhält der Staat bei der dargestellten Tankfüllung an Steuern? Kreuze die richtige Antwort an.

(!15,80€) (!34,47€) (42,71€) (!73,-€) (!90,45€)

Aufgabe 4: Zapfsäule 2

Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. Petra stellt fest: "Wenn der Staat überhaupt keine Steuern auf Benzin mehr erheben würde, würde der Benzinpreis auf etwa ein Viertel des jetzigen Preises sinken."

Erkläre, wie Petra zu dieser Aussage kommt.

  • 1 Euro - 73 Cent = 27 Cent, das entspricht ca. 25% bzw. 1/4.
  • 73 Cent pro Euro bedeutet 73% Steuern, also etwa 3/4. Also etwas 1/4 ohne Steuern.
  • 74200 + 46500 Euro = 120700 Euro

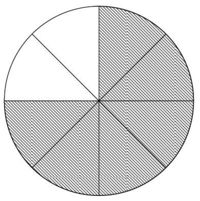
Aufgabe 5: Kreis

AufgabeA5 Kreis.jpg

Wie viel Prozent des Kreises wurden eingefärbt?

Kreuze die richtige Lösung an. (!30%) (!45%) (!60%) (!70%) (75%) (!95%)

Aufgabe 6: Gleichung

Du siehst hier folgende Aufgabe: 248 + 146 + 320 =

Das Ergebnis der Aufgabe ist eine gerade Zahl.

Erkläre, warum das so ist, ohne das Ergebnis auszurechnen.

zum Beispiel:

  • 248, 146, 320 sind gerade Zahlen. werden diese Zahlen addiert, dann ist auch das Ergebnis eine gerade Zahl
  • In den Zahlen sind nur gerade Zahlen.

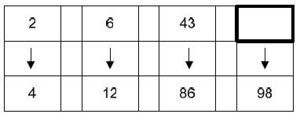
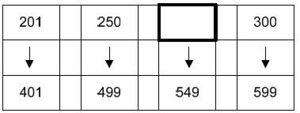
Aufgabe 7: Welche Zahl fehlt?

Trage die fehlende Zahl ein!

1.AufgabeA7 Zahl1.jpg

2. AufgabeA7 Zahl2.jpg

  1. 49
  2. 275


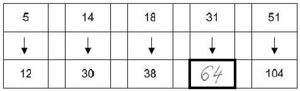
3. Timo schreibt die Zahl 64 zur 31. Das ist die richtige Lösung! Schreibe auf, wie Timo die Zahl 64 gefunden hat.

AufgabeA7 Zahl3.jpg

"Obere Zahl mal 2 und dann plus 2" oder "Obere Zahl plus 1 und dann mal 2"

Aufgabe 8: Ziffer 5

Peter hat nacheinander alle Zahlen von 1 bis 99 notiert.

Wie oft hat er dabei die Ziffer 5 geschrieben?

20 mal

Wie viele Ziffern hat Peter insgesamt geschrieben?

189 Ziffern

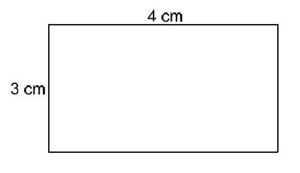
Aufgabe 9: Rechteck

Ein Rechteck ist 4 cm lang und 3 cm breit.

AufgabeA9 Rechteck.jpg

Wie groß ist sein Flächeninhalt?

Kreuze an.

(12cm2) (!7 cm) (!7 cm2) (!12 cm) (!14 cm)

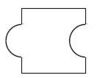
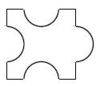
Aufgabe 10: Puzzleteile

Welches dieser Puzzleteile hat den größten Flächeninhalt? Kreuze an.

(!AufgabeA10 Puzzle1.jpg) (!AufgabeA10 Puzzle2.jpg) (!AufgabeA10 Puzzle3.jpg) (!AufgabeA10 Puzzle4.jpg) (AufgabeA10 Puzzle5.jpg)

Aufgabe 11: Saft

Für wie viele Gläser reicht die Flasche? AufgabeA11 Saft.jpg

Die Flasche reicht für 10 Gläser Saft.

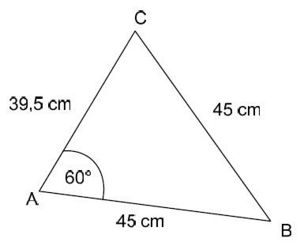
Aufgabe 12: Das unmögliche Dreieck

Begründe, warum es kein Dreieck mit diesen Maßen geben kann.

AufgabeA12 Dreieck.jpg

z.B.: Das Dreieck ABC ist gleichschenklig und hat einen Innenwinkel von 600. Folglich müsste dieses Dreieck gleichseitig sein. Daher müssten alle Seiten entweder 39,5 cm oder 45 cm lang sein.

Aufgabe 13: Geld umrechnen

Rechne um:

27 € 50 Cent = ..... Euro

27 € 50 Cent = 27,50 Euro

1 € 1 Cent = ..... Cent

1 € 1 Cent = 101 Cent

Aufgabe 14: Minuten und Sekunden

Rechne die Zeitangaben um und fülle die Lücken aus. Beispiel: 95 s = 1 min 35s

..... s = 3 min 28 s

208 s = 3 min 28 s

136 s = ..... min ..... s

136 s = 2 min 16 s

..... s = 8 min 20 s

500 s = 8 min 20 s

Aufgabe 15: Fehlendes Zeichen

Ordne zu:

< 5m ... 5,50 m 0, 8 cm ... 100 mm
> 20 cm ... 20 mm 700 cm ... 17 cm
= 180 cm ... 1,80 m 4 cm ... 40 mm

Aufgabe 16: Winkel im Dreieck

Abgerufen von „https://unterrichten.zum.de/index.php?title=Benutzer:Uschuetzenmeister/Test_Uwe/Lernmodule_Maria&oldid=100529“