Vektorrechnung/WHG Q1 Einstieg Rechnen mit Vektoren: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (16 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Führt man zwei Verschiebungen hintereinander aus, so ergibt sich wieder eine neue Verschiebung. In Abbildung | Führt man zwei Verschiebungen hintereinander aus, so ergibt sich wieder eine neue Verschiebung. In der Abbildung werden die Verschiebungen der Vektoren | ||
<math> | <math> | ||
\ | \vec{AB} = \begin{pmatrix}3\\4\end{pmatrix} | ||
</math> | </math> | ||
und | |||
<math> | |||
\vec{BC} = \begin{pmatrix}4\\1\end{pmatrix} | |||
</math> | |||
hintereinander ausgeführt. Zum gleichen Endzustand gelangt man jedoch auch, wenn nur die Verschiebung des Vektors <math>\vec{AC}</math> ausgeführt wird. | |||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 10: | Zeile 14: | ||
|Aufgabe | |Aufgabe | ||
| | | | ||
* Geben Sie die Koordinaten des Vektors <math>\vec{AC}</math> an. | |||
* Stellen Sie eine Vermutung zur Beziehung zwischen dem Vektor <math>\vec{AC}</math> und den Vektoren <math>\vec{AB}</math> und <math>\vec{BC}</math> auf. Notieren Sie Ihre Hypothese. Vergleichen Sie anschließend mit der Lösung. | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Lösung versteckt|<math>\vec{AC}=\begin{pmatrix}7\\5\end{pmatrix}=\begin{pmatrix}3\\4\end{pmatrix}+\begin{pmatrix}4\\1\end{pmatrix}=\vec{AB}+\vec{BC}</math>}} | |||
| | | | ||
[[Datei:Abbildung 1.png|200|center|Abbildung 1]] | [[Datei:Abbildung 1.png|200|center|Abbildung 1]] | ||
}} | }} | ||
<br> | <br> | ||
<br> | |||
{{Fortsetzung|weiter=Vektoraddition|weiterlink=WHG_Q1_Vektorrechnung/WHG_Q1_Vektoraddition|vorher=Übersicht|vorherlink=WHG_Q1_Vektorrechnung/WHG_Q1_Rechnen mit Vektoren}} | {{Fortsetzung|weiter=Vektoraddition|weiterlink=WHG_Q1_Vektorrechnung/WHG_Q1_Vektoraddition|vorher=Übersicht|vorherlink=WHG_Q1_Vektorrechnung/WHG_Q1_Rechnen mit Vektoren}} | ||
Version vom 17. September 2020, 09:42 Uhr
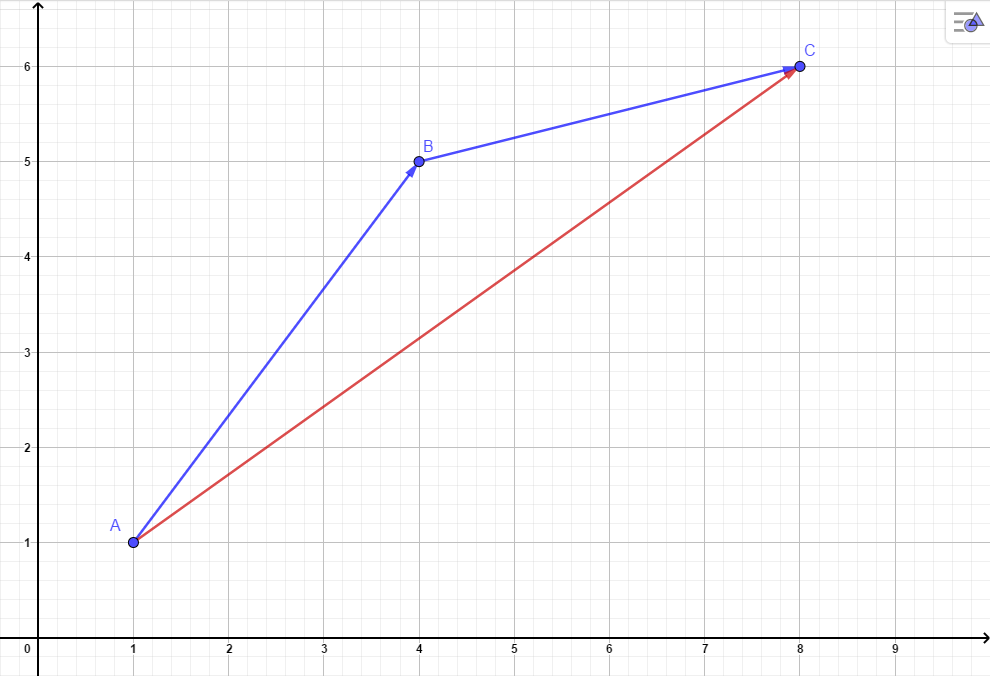
Führt man zwei Verschiebungen hintereinander aus, so ergibt sich wieder eine neue Verschiebung. In der Abbildung werden die Verschiebungen der Vektoren
und
hintereinander ausgeführt. Zum gleichen Endzustand gelangt man jedoch auch, wenn nur die Verschiebung des Vektors ausgeführt wird.
Aufgabe
- Geben Sie die Koordinaten des Vektors an.
- Stellen Sie eine Vermutung zur Beziehung zwischen dem Vektor und den Vektoren und auf. Notieren Sie Ihre Hypothese. Vergleichen Sie anschließend mit der Lösung.