Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Vorwissen
Zufallsexperiment
Versuche dich zu erinnern und schreibe eine möglichst genaue Beschreibung des Begriffs "Zufallsexperiment" auf. Informiere dich wenn nötig in deinen Unterlagen aus der Schule oder recherchiere im Internet danach.
(Ziehung der Lottozahlen) (Schere, Stein, Papier) (!Wettervorhersage) (!Elfmeterschießen im WM-Finale) (dreimaliges Werfen eines Würfels) (ein Marmeladenbrot fällt vom Tisch) (!Benotung deiner Klassenarbeit) (Werfen einer Münze) (Werfen eines gezinkten Würfels) (!Geschwindigkeitsmessung der Polizei) (!physikalisches Experiment)
Hinweis: Du kannst das Multiplechoice-Quiz nochmal versuchen, indem du nach Aufgabe 1.5 die Buttons „Korrektur“ und „Neustart“ anklickst!
Durch Markieren der grauen Fläche wird ein Lösungsvorschlag sichtbar: Es wird festgelegt, dass die Münze auf den gebeugten Zeigefinger gelegt und mit dem Daumen in die Luft geschnipst werden soll. Die Münze wird gefangen und auf den Handrücken gelegt. Die Seite gewinnt, welche nach der Landung oben liegt.
Ergebnis und Ereignis
Zur korrekten mathematischen Beschreibung von Zufallsexperimenten benötigt man eine formale Sprache.
In der folgenden Aufgabe, kannst du am Beispiel des Würfelwurfs kontrollieren, ob du die richtige Schreibweise beherrschst.
| Ergebnis | 6 | |
| Ereignis | ||
| Elementarereignis | ||
| Ergebnismenge | ||
| Gegenereignis | ||
| unmögliches Ereignis | ||
| Mächtigkeit des Ergebnisraums |
Lösungshinweise:
Vorlage:Versteckt
Lösungshinweise:
Vorlage:Versteckt
Lösungshinweise: Vorlage:Versteckt
Lösung:
Laplace-Wahrscheinlichkeit
Pierre-Simon Laplace![]() (1749 - 1827) war ein Physiker und Mathematiker, unter anderem auch am Hofe Napoleons.
<br!> Er beschäftigte sich mit der Wahrscheinlichkeitsrechnung, vor allem in Verbindung mit dem Glücksspiel.
(1749 - 1827) war ein Physiker und Mathematiker, unter anderem auch am Hofe Napoleons.
<br!> Er beschäftigte sich mit der Wahrscheinlichkeitsrechnung, vor allem in Verbindung mit dem Glücksspiel.
Lösungshilfe: Vorlage:Versteckt
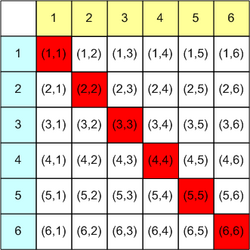
- Man kann aus der Tabelle prima die Ergebnismenge und das Ereignis „Pasch“ ablesen:
- Man sagt dazu „36-Feldertafel“, auf Grund der Mächtigkeit der Ergebnismenge.