Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Efron: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Florian Bogner |
Main>Florian Bogner |
||
| Zeile 14: | Zeile 14: | ||
{{Aufgaben-M|1|Findest du das Spiel fair?}} | {{Aufgaben-M|1|Findest du das Spiel fair?}} | ||
Um dies herauszufinden, bastle dir die „Würfel von Efron“ ganz einfach nach. Nimm dazu beispielsweise vier helle Spielwürfel und beschrifte diese mit einem Folienstift so wie oben dargestellt. | Um dies herauszufinden, bastle dir die „Würfel von Efron“ ganz einfach nach. Nimm dazu beispielsweise vier helle Spielwürfel und beschrifte diese mit einem Folienstift so wie oben dargestellt. Jetzt spiele mit einem Freund oder einer Freundin nach den '''Spielregeln'''. | ||
Jetzt spiele mit einem Freund | |||
{{Lösung versteckt|Wie ihr sicherlich herausgefunden habt, scheinen manche Würfel besser zu sein als andere. Wenn du die nächsten Aufgaben bearbeitest, wirst du erkennen, dass man mit einer gewissen Taktik sein Glück in diesem Spiel ganz schön beeinflussen kann.}} | {{Lösung versteckt|Wie ihr sicherlich herausgefunden habt, scheinen manche Würfel besser zu sein als andere. Wenn du die nächsten Aufgaben bearbeitest, wirst du erkennen, dass man mit einer gewissen Taktik sein Glück in diesem Spiel ganz schön beeinflussen kann.}} | ||
| Zeile 23: | Zeile 21: | ||
{{Aufgaben-M|2|Kannst du Ergebnisräume angeben, sodass es sich beim Wurf mit den „Würfeln von Efron“ um ein Laplace-Experiment handelt?}} | {{Aufgaben-M|2|Kannst du Ergebnisräume angeben, sodass es sich beim Wurf mit den „Würfeln von Efron“ um ein Laplace-Experiment handelt?}} | ||
{{Lösung versteckt|zum Beispiel | {{Lösung versteckt|Eine richtige Lösung ist zum Beispiel <math> \Omega_{gruen} = \left\{ 4_1, 4_2, 4_3, 4_4, 0_1, 0_2 \right\} </math> für den grünen Würfel. Da jede Seite gleichwahrscheinlich ist, ist zum Beispiel die Wahrscheinlichkeit eine Null zu würfeln <math>p\left(0\right)=\frac{2}{6}=\frac{1}{3}</math> . | ||
Falsche Lösung: <math> \Omega = \left\{ 4, 0 \right\} </math>. Hier sind die Ergebnisse nicht gleichwahrscheinlich! | |||
}} | |||
{{Aufgaben-M|3|Pia | {{Aufgaben-M|3|Pia ist höflich und lässt Anna den Vortritt. Anna sucht sich den roten Würfel aus, weil das ihre Lieblingsfarbe ist. Danach nimmt Pia den grünen Würfel. | ||
Wer hat die besseren Gewinnchancen? Berechne die Gewinnwahrscheinlichkeiten für Pia und Anna.}} | Wer hat die besseren Gewinnchancen? Berechne die Gewinnwahrscheinlichkeiten für Pia und Anna.}} | ||
Lösungshinweise: {{versteckt|* Erstelle ein Baumdiagramm. | |||
* Die erste Stufe ist z.B. Pias Wurf, die zweite Stufe ist dann Annas Wurf. | |||
* Berechne die dazugehörigen Wahrscheinlichkeiten wie in Aufgabe 2.}} | |||
{{Lösung versteckt|Da Anna sicher eine 3 würfelt, gewinnt sie nur wenn Pia eine 0 würfelt. Nach Aufgabe 2 ist diese Wahrscheinlichkeit <math>\frac{ | {{Lösung versteckt|Da Anna sicher eine 3 würfelt, gewinnt sie nur wenn Pia eine 0 würfelt. Nach Aufgabe 2 ist diese Wahrscheinlichkeit <math>p\left(0\right)=\frac{1}{3}</math> . Das Ereignis „Pia gewinnt“ ist das Gegenereignis dazu und berechnet sich demnach so: <math>p(Pia)=1-\frac{1}{3}=\frac{2}{3}</math> . | ||
Dies lässt sich aus dem folgenden Baumdiagramm erkennen: | Dies lässt sich aus dem folgenden Baumdiagramm erkennen: | ||
| Zeile 53: | Zeile 56: | ||
{{Aufgaben-M|6|Hans und Franz wollen bei Pia und Anna mitspielen. Wie groß ist die Wahrscheinlichkeit für jeden der Würfel, dass er gewinnt, wenn alle vier Würfel geworden werden?}} | {{Aufgaben-M|6|Hans und Franz wollen bei Pia und Anna mitspielen. Wie groß ist die Wahrscheinlichkeit für jeden der Würfel, dass er gewinnt, wenn alle vier Würfel geworden werden?}} | ||
Hilfe: {{versteckt|Jetzt musst du ein Baumdiagramm mit vier Stufen entwerfen. Zeichne so wenige | Hilfe: {{versteckt|Jetzt musst du ein Baumdiagramm mit vier Stufen entwerfen. Zeichne so wenige Zweige wie möglich, damit es übersichtlich bleibt.}} | ||
Version vom 2. September 2009, 09:14 Uhr
Die „Würfel von Efron“
Um dies herauszufinden, bastle dir die „Würfel von Efron“ ganz einfach nach. Nimm dazu beispielsweise vier helle Spielwürfel und beschrifte diese mit einem Folienstift so wie oben dargestellt. Jetzt spiele mit einem Freund oder einer Freundin nach den Spielregeln.
Wie ihr sicherlich herausgefunden habt, scheinen manche Würfel besser zu sein als andere. Wenn du die nächsten Aufgaben bearbeitest, wirst du erkennen, dass man mit einer gewissen Taktik sein Glück in diesem Spiel ganz schön beeinflussen kann.
Eine richtige Lösung ist zum Beispiel für den grünen Würfel. Da jede Seite gleichwahrscheinlich ist, ist zum Beispiel die Wahrscheinlichkeit eine Null zu würfeln .
Falsche Lösung: . Hier sind die Ergebnisse nicht gleichwahrscheinlich!
Lösungshinweise: Vorlage:Versteckt
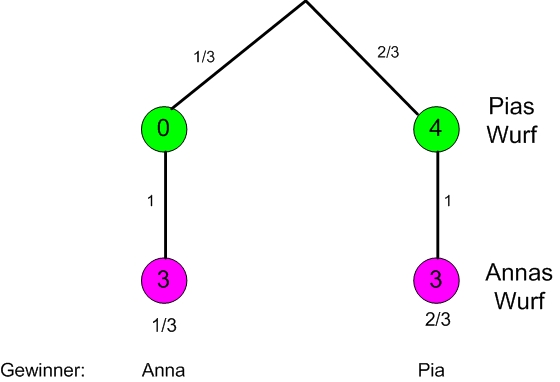
Da Anna sicher eine 3 würfelt, gewinnt sie nur wenn Pia eine 0 würfelt. Nach Aufgabe 2 ist diese Wahrscheinlichkeit . Das Ereignis „Pia gewinnt“ ist das Gegenereignis dazu und berechnet sich demnach so: .
Dies lässt sich aus dem folgenden Baumdiagramm erkennen:
Tipp: Überlege dir alle Möglichkeiten mit zwei Würfeln gegeneinander zu spielen.
Hilfe: Vorlage:Versteckt
