Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Drei-Würfel-Problem: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Florian Bogner |
Main>Florian Bogner (gustav weg) |
||
| Zeile 21: | Zeile 21: | ||
{{Aufgabe|Welchen Fehler hatte ''de Méré'' wohl gemacht? Kannst du den Irrtum aufklären?}} | {{Aufgabe|Welchen Fehler hatte ''de Méré'' wohl gemacht? Kannst du den Irrtum aufklären?}} | ||
{{Aufgaben-M|2|Berechne die Wahrscheinlichkeiten der Augensummen 11 und 12 beim zweifachen Würfelwurf! | {{Aufgaben-M|2|Berechne die Wahrscheinlichkeiten der Augensummen 11 und 12 beim zweifachen Würfelwurf! | ||
Version vom 3. September 2009, 16:22 Uhr
Das „Drei-Würfel-Problem“
Bild von drei Würfeln einfügen!
Aufgabe
Welchen Fehler hatte de Méré wohl gemacht? Kannst du den Irrtum aufklären?
Tipp: Was fällt dir an den Würfeln im Spiel auf? Zeichne ein Baumdiagramm für die Augensummen 11 und 12 beim zweifachen Würfelwurf.
Die Würfel sind unterschiedlich gefärbt. Man könnte auch sagen: 1. Wurf ist rot, 2. Wurf ist grün.
Damit wäre die Lösung nach de Méré der Art, dass es eine Möglichkeit für beide Augensummen gibt, nämlich beziehungsweise , falsch.
Das Baumdiagramm zeigt zwei Wege, welche die Augensumme 11 ergeben. <br!>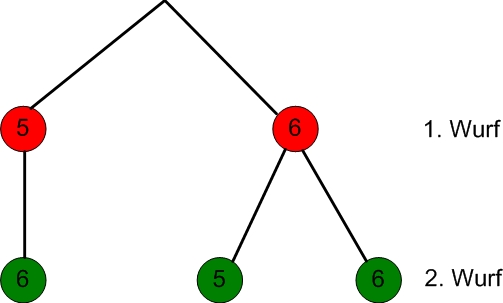
Aufgabe
Löse nun Aufgabe 1, indem du die Wahrscheinlichkeiten für die gesuchten Augensummen beim dreifachen Würfelwurf berechnest.
Lösungshilfen:
- Erstelle die Ergebnismenge, wie de Méré es gemacht hat. Handelt es sich mit dieser Ergebnissmenge um ein Laplaceexperiment?
- Stelle dir vor die Würfel wären unterschiedlich. (Bild!)
- Mit Hilfe dieser Urnensimulation kannst du unter anderem einen dreifachen Würfelwurf simulieren. Führe dies mit und ohne Beachtung der Reihenfolge durch. Was fällt dir auf?
Vorlage:Rechtsklick Fenster Urnensimulation
(→ Wie geht das?) Vorlage:Versteckt
- Erstelle nun die Ergebnismenge, sodass es sich um ein Laplace-experiment handelt! Jetzt kannst du unter der Voraussetzung der Gliechwahrscheinlichkeit die gesuchten Wahrscheinlichkeiten berechnen.



