Die Druckversion wird nicht mehr unterstützt und kann Darstellungsfehler aufweisen. Bitte aktualisiere deine Browser-Lesezeichen und verwende stattdessen die Standard-Druckfunktion des Browsers.
Lernpfad zur Logarithmusfunktion
Info zur Bearbeitung
Bearbeitet die folgenden Aufgaben zur Logarithmusfunktion. Was ihr jeweils zu tun habt steht in der Aufgabenstellung. Teilweise gibt es Buttons mit "Tipp" und "Lösung". Wenn ihr auf diese klickt, öffnet sich entsprechend ein Tipp zur Bearbeitung oder die Lösung der Aufgabe.
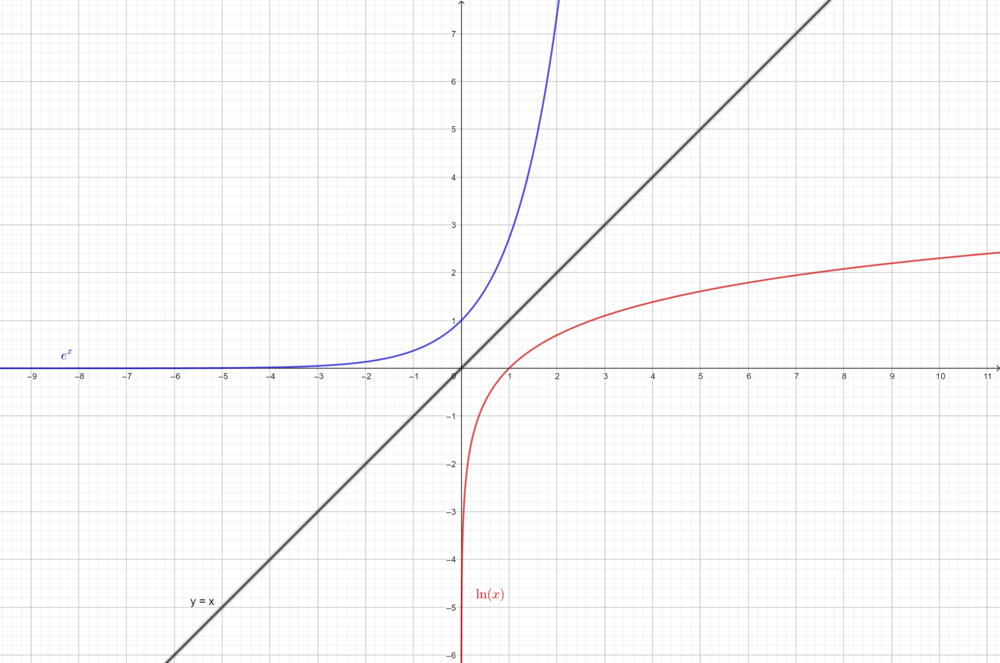
1. Erkundung der Logarithmusfunktion
2. Nice to know!
Was ist der Logarithmus überhaupt?
3. Die Ableitung des natürlichen Logarithmus
Auch die Ableitung von  kann mit Hilfe der obigen Ableitungsregel für Umkehrfunktionen berechnet werden.
kann mit Hilfe der obigen Ableitungsregel für Umkehrfunktionen berechnet werden.
Aufgabe: Leite mit Hilfe dieser Ableitungsregel den natürlichen Logarithmus ab.
Da

ist, ist

und

. Setzte diese entsprechend (teilweise ja die Ableitung) in die Formel

ein.
4. Ein paar Ableitungen zum "warm" werden.
Berechne von den folgenden Funktionen jeweils die erste und zweite Ableitung in deinem Heft.
Beachte, dass bei  -Funktionen meistens die Ketten-, Produkt- und Quotientenregel zum Ableiten gebraucht werden. Falls du diese nicht mehr kennst, kannst du jeweils in dem entsprechenden Tipp nachschauen.
-Funktionen meistens die Ketten-, Produkt- und Quotientenregel zum Ableiten gebraucht werden. Falls du diese nicht mehr kennst, kannst du jeweils in dem entsprechenden Tipp nachschauen.
a) 
b) 
c) 
*d) 

, dann


, dann


, dann

1. Möglichkeit: Die Logarithmusregel  kann hierbei helfen. Du musst nur noch überlegen, wie du den
kann hierbei helfen. Du musst nur noch überlegen, wie du den  eingebaut bekommst, ohne den Wert der Funktion zu ändern.
eingebaut bekommst, ohne den Wert der Funktion zu ändern.
2. Möglichkeit (etwas schwieriger): Es hilft ein kleiner Trick. Nehmt von beiden Seiten den

, also

, berechnet dann von beiden Seiten die Ableitung und formt die Gleichung am Ende geschickt um.
1. Ableitung: (Kettenregel) 
2. Ableitung:

1. Ableitung: (Produktregel) 
2. Ableitung:
(Produktregel) 
1. Ableitung: (Quotientenregel) 
2. Ableitung: (Quotientenregel) 
Also ist  und
und 
Zudem ist  und
und 
Daher folgt:

1. Möglichkeit:
1. Ableitung: 
2. Möglichkeit:
1. Ableitung:

2. Ableitung:
(Produktregel) 
5. Ableiten verschiedener

-Funktionen
Leite die folgenden (orangenen) Funktionen in deinem Heft ab und ordne sie dann ihrer Ableitung zu. Löse die Aufgabe nicht durch Ausprobieren! Notiere die eventuelle Fragen oder Unklarheiten.
6. Die Stammfunktion des natürlichen Logarithmus
Die Stammfunktion des natürlichen Logarithmus ist definiert durch:
 .
.
(Die Integration kann man mit Hilfe partieller Integration durchführen.)
Aufgabe: Weise nach, dass die obige Funktion  die Stammfunktion von
die Stammfunktion von  ist.
ist.
Leite

ab.

7. Kurvendiskussion ohne GTR
Gegeben ist die Funktion  .
.
a) Untersuche diese hinsichtlich des Definitionsbereiches, der Symmetrie, der Schnittpunkte mit den Koordinatenachsen, dem Unendlichkeitsverhalten der Extrempunkte und der Wendepunkte.
Sofern

eine irrationale Zahl ist, lasst diese einfach in der Form von

stehen.
Bei gleicher Basis werden bei der Multiplikation die Exponenten addiert:

, bei der Division die Exponenten subtrahiert:

und bei der Potenzierung die Exponenten multipliziert:

. Zudem kann man

bei gleichem Exponenten ausklammern.
Um den Definitionsbereich festzulegen, muss man sich die Funktion anschauen und begutachten, ob es durch die verschiedenen Funktionsbestandteile Einschränkungen für

gibt. Man muss also schauen welche

man einsetzten darf und welche nicht.
Eine Funktion ist punktsymmetrisch, falls  gilt.
gilt.
Eine Funktion ist achsensymmetrisch, falls

gilt.


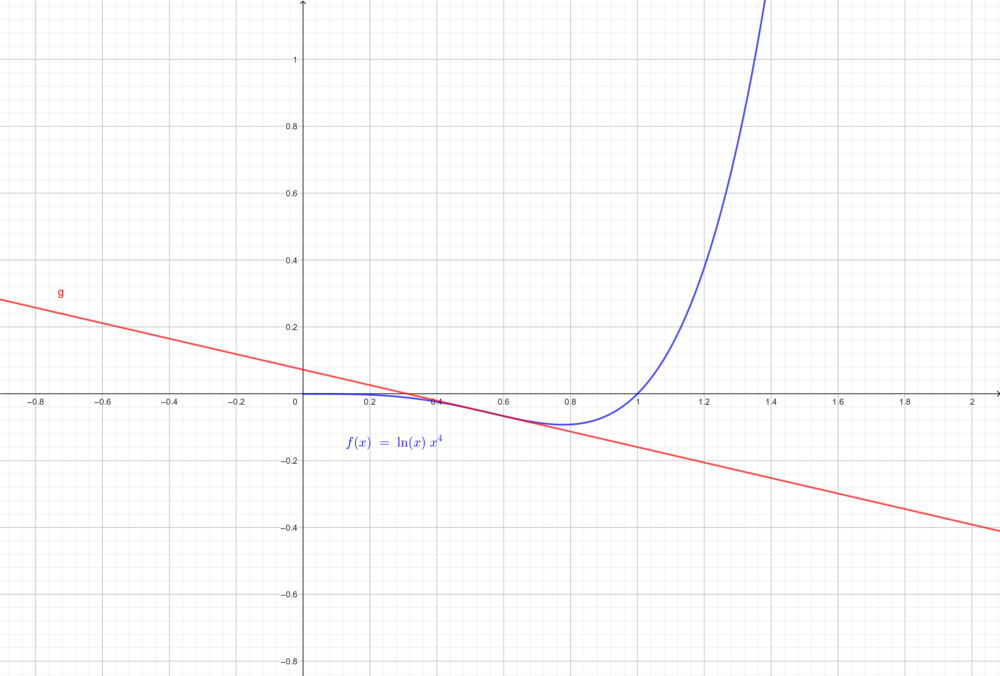
b) Die Wendetangente  begrenzt mit den Koordinatenachsen ein Flächenstück im 1. Quadranten. Berechne den Flächeninhalt dieses Stückes.
begrenzt mit den Koordinatenachsen ein Flächenstück im 1. Quadranten. Berechne den Flächeninhalt dieses Stückes.
Die Wendetangente ist die Tangente, die den Funktionsgraphen am Wendepunkt berührt. Dementsprechend stimmt der dortige Ableitungswert mit der Steigung der Tangenten überein.
Das Flächenstück, welches eine Gerade mit den Koordinatenachsen einschließt, ist ein Dreieck.