Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Infos für Lehrkräfte

Handreichung für Lehrkräfte

In diesem Lernpfad werden Grundvorstellungen zum Ableitungsbegriff behandelt. Der Lernpfad ist so Aufgebaut, dass sich Schülerinnen und Schüler die

• Ableitung als momentane Änderungsrate
• Ableitung als Steigung der Tangente
• Ableitung als lokale lineare Approximation

Selbst erarbeiten können. Die Ableitung als Änderungsdetektor wird als ergänzende Grundvorstellung behandelt.

In dieser Handreichung werden nun Möglichkeiten aufgezeigt wie der Lernpfad in den Unterricht eingebaut werden kann, was bei den einzelnen Grundvorstellungen zu beachten ist und wieso es Sinn macht, dass Schülerinnen und Schüler diesen Lernpfad bearbeiten.

Im Lernpfad sind zu allen gestellten Aufgaben die benötigten Voraussetzungen, Lösungen und passenden Hilfestellungen vorhanden.   

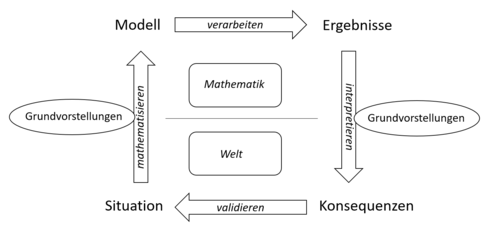
Grundvorstellungen

Modellierungsprozess

Grundvorstellungen sind Instrumente der Vermittlung zwischen Mathematik und Realität. Sie weisen mathematischen Begriffen eine inhaltliche Deutung und Sinnhaftigkeit zu, was eine wesentliche Voraussetzungen für einen verständnisvollen Umgang mit Begriffen darstellt. Mit diesen Eigenschaften spielen sie eine zentrale Rolle bei der mathematischen Modellierung und greifen im Modellierungskreislauf beim Prozess der Mathematisierung und der Interpretation.

Hinweise zu den Grundvorstellungen

Wird der Lernpfad in den Unterricht eingebunden so ist bei Gruppenreflexionen oder Sicherungen der Aufgaben auf folgenden Punkte zu achten.

Ableitung als Steigung der Tangente

• Erweiterung des Tangentenbegriffs als lokale Schmiegegerade.

• Vermeidung der Sichtweise die Tangente schneide den Graph nur in einem Punkt.

• Die Tangente hat die gleiche Steigung wie der Graph an dem Punkt den sie berührt.

Ableitung als momentane Änderungsrate

• Das mit dem Zeug auf allen Ebenen

Ableitung als lineare Approximation

• In einer stark Vergrößerten Umgebung eines Punktes des Graphen einer differenzierbaren Funktion ist dieses Teilstück des Graphen geradlinig.

• Da eine differenzierbare Funktion in hinreichend kleinen Umgebungen linear ist, kann sie in dieser Umgebung durch die Tangente genähert werden.

Möglichkeiten der Einbindung

• Da es sich hier um einen Wiki - Lernpfad handelt, können verschiedene Aufgaben aus dem Lernpfad herauskopiert werden und an die Anforderungen der eigenen Lerngruppe angepasst werden. So können auch einzelne Aufgaben des Lernpfads im Unterricht bearbeitet werden.

• Es kann jede Grundvorstellung allein stehend von den Schülern selbst erarbeitet werden und kann somit als Hausaufgabe oder Wochenaufgabe aufgegeben werden.

• Die Aufgaben des Lernpfads sind auch auf folgenden Arbeitsblättern festgehalten und können den Schülern somit ausgedruckt werden. So benötigt lediglich die Bedienung der Applets ein PC oder Tablet. Dies kann bei mangelnder Ausstattung von Vorteil sein.

Hinweise zu den Aufgaben

Das Ziel jeder Aufgabe des Lernpfads ist es, durch angeleitetes Selbsterkunden in den Applets oder mithilfe von Tabellen und Graphiken Erkenntnisse zu gewinnen. Trotz eingebauter Hilfestellungen und Lösungskontrollen ist es gerade bei der Vermittlung von Grundvorstellung wichtig die selbstgewonnen Erkenntnisse mit denen von Anderen zu vergleichen und somit auf ihre mathematische Korrektheit zu überprüfen. Es wird daher empfohlen an geeigneten Stellen gemeinsame Sicherungs- oder Reflexionsphasen einzubauen.