Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Ziegen

Das „Ziegenproblem“

In einer Quizshow kann sich der Kandidat zwischen drei Türen entscheiden. Hinter einer wartet ein Hauptgewinn, z. B. ein Auto. Hinter den beiden anderen steht als Niete jeweils eine Ziege. Hat sich der Kandidat für eine Tür entschieden, bietet ihm der Moderator einen Deal an: Zuerst öffnet er in jedem Fall eine der beiden übrigen Türen und eine Ziege kommt zum Vorschein. Dann fragt er den Kandidaten, ob er nun nicht lieber die Tür wechseln will.

Aufgabe

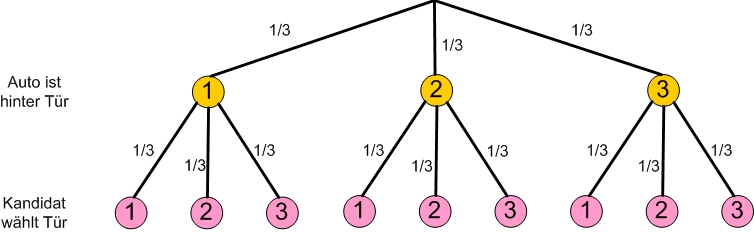
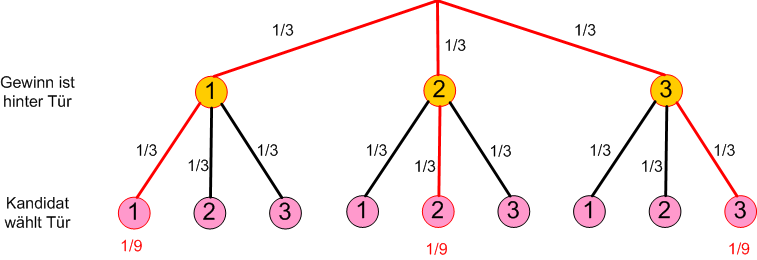
Ist es vorteilhaft für den Kandidaten zu wechseln? Löse die Aufgabe mit einem Baumdiagramm!

---

• Oder hast du das „Ziegenproblem“ noch nicht so richtig verstanden?

Dann öffne folgende Seite mit einer anschaulichen Beschreibung in einem neuen Fenster. Betrachte aber noch nicht die Lösung!

Ziegenproblem anschaulich erklärt

• Hast du dir schon überlegt, ob sich die Wahrscheinlichkeit beim Wechseln ändert und möchtest deine Hypothese überprüfen?

Oder möchtest du einfach die Quiz-Show nachspielen?

Dann öffne das Java-Applet und spiele das „Ziegenproblem“ nach! Die Türen öffnen sich durch anklicken. „Reset Doors“ schließt die Türen wieder.

Versuche dich an zwei Strategien: Behalte deine ausgewählte Tür oder wechsle die Tür jedes mal.

Ziegenproblem, nur mit Schweinchen

---

→ Versuche dich nun selbst an der Lösung des „Ziegenproblems“!

Aufgabe 5.1

Bevor die Show beginnt, wird das Auto hinter eine zufällig bestimmte Tür gestellt. Mit welcher Wahrscheinlichkeit wird jeweils eine der drei Türen ausgewählt? Zeichne ein Baumdiagramm!

Das Auto steht hinter jeder Tür mit einer Wahrscheinlichkeit von $\frac{1}{3}\ .$

Aufgabe 5.2

Mit welcher Wahrscheinlichkeit wählt der Kandidat sofort die Tür mit dem Hauptgewinn? Erweitere dein Baumdiagramm aus Aufgabe 5.1.

Der Kandidat wählt sofort die Tür mit dem Hauptgewinn mit einer Wahrscheinlichkeit von $\frac{1}{3}\ .$

Aufgabe 5.3

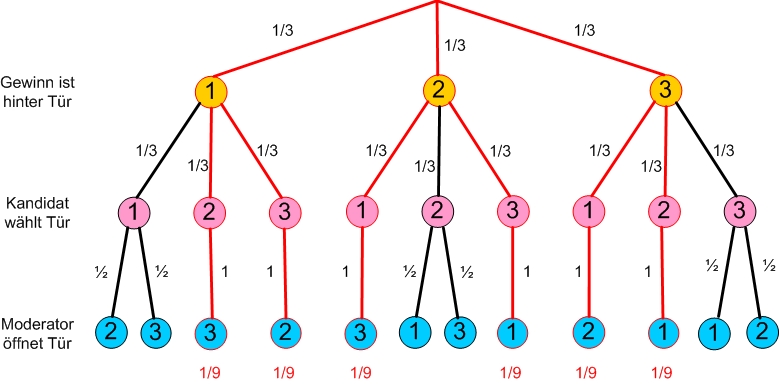
Der Moderator öffnet nun eine der nicht gewählten Türen, aber natürlich nicht die mit dem Auto. Mit welcher Wahrscheinlichkeit steht das Auto hinter der anderen Tür? Erweitere auch hier dein Baumdiagramm.

Hier gibt es verschiedene Fälle, je nachdem, wo der Hauptgewinn steht und welche Tür der Kandidat wählt.

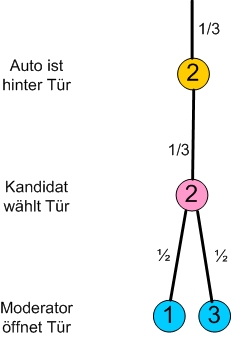
• 1. Fall: Hat der Kandidat bereits die Tür mit dem Auto gewählt, öffnet der Moderator zufällig eine der beiden anderen Türen.

Beispiel: Der Kandidat hat zufällig Tür 2 mit dem Hauptgewinn gewählt. Der Moderator öffnet nun zufällig Tür 1 oder 3.

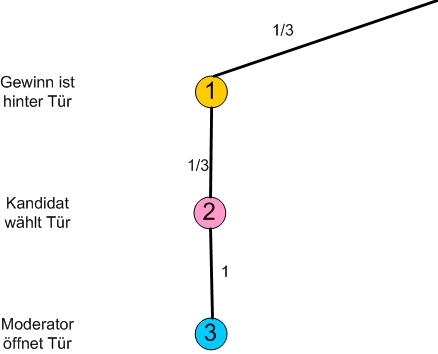
• 2. Fall Steht hinter der gewählten Tür eine Ziege, kann der Moderator nur eine Tür öffnen.

Beispiel 2: Das Auto steht hinter Tür 1. Der Kandidat wählt Tür 2. Der Moderator muss Tür 3 öffnen.

Lese die Wahrscheinlichkeiten im Baudiagramm ab:

Aufgabe 5.4

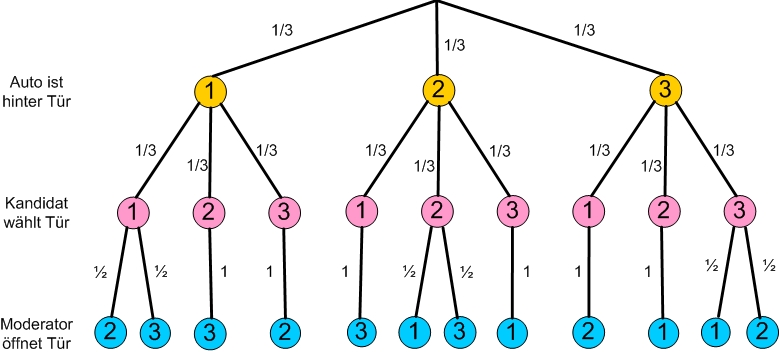
Löse nun das „Ziegenproblem“. Berechne dazu die Wahrscheinlichkeiten der Pfade. Kannst du jetzt die Frage beantworten, ob sich ein Wechsel lohnt oder nicht?

Betrachte die Pfade, bei denen der Kandidat sein Tor behält und jene, bei denen er wechselt.

• Addiere die Wahrscheinlichkeiten der Pfade, bei denen der Kandidat gewinnt, wenn er prinzipiell die Tür wechselt. So erhälst du die Gewinnwahrscheinlichkeit „mit Wechsel“:

$\Rightarrow \quad p(\mathrm{Gewinn\ mit\ Wechsel})=6 \cdot \frac{1}{9}=\frac{2}{3}$

• Betrachten wir nun noch die Gegenwahrscheinlichkeit: die Gewinnwahrscheinlichkeit „ohne Wechsel“. Der Kandidat gewinnt in diesem Fall nur, wenn er sofort die richtige Tür wählt:

$\Rightarrow \quad p(\mathrm{Gewinn\ ohne\ Wechsel})=3 \cdot \frac{1}{9}=\frac{1}{3}$

• Fazit: Wenn man die Türe wechselt, so verdoppelt sich die Gewinnwahrscheinlichkeit von   $\frac{1}{3}$  auf  $\frac{2}{3}$  . Es ist also vorteilhaft, die Tür noch einmal zu wechseln.

---

Für Interessierte:

Interessiert dich das Ziegenproblem genauer, oder leuchtet dir die Lösung noch nicht ein?

• Öffne noch einmal das Ziegenproblem, nur mit Schweinchen. Du kannst die Anzahl der Türen erhöhen: Schiebe den Regler „Number of doors“ weiter nach rechts. Hast du eine Tür gewählt, öffnet der Moderator alle anderen Türen, bis auf die mit dem Hauptgewinn.

Würdest du jetzt wechseln???

• Unter dem Wikipedia-Link kannst du dich noch genauer über die Hintergründe des Ziegenproblems informieren:

---

Herzlichen Glückwunsch! Du hast nun dein Wissen über die Laplace-Wahrscheinlichkeit erweitert.

---

Laplace-Wahrscheinlichkeit wiederholen und vertiefen

1. Zufallsexperiment, Ergebnis und Ereignis, Laplace-Wahrscheinlichkeit
2. „Gustavs Glücksspiel“
   
3. Das „Drei-Würfel-Problem“
4. Die „Würfel von Efron“
5. Das „Ziegenproblem“