Einführung in die Integralrechnung
In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken.
Einige Übungen sind dem gleichnamigen Lernpfad Einführung in die Integralrechnung der österreichischen Arbeitsgruppe Medienvielfalt im Mathematikunterricht entnommen, die aus einer Kooperation von mathe-online und GeoGebra entstanden ist.
Materialien:
Das Flächenproblem
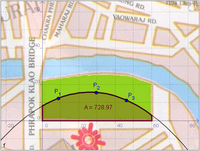
Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können.
- Wie groß ist der Wasserverbrauch?
- Wie groß ist der Flächeninhalt des Grundstücks?
Unter- und Obersumme
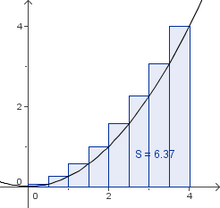
- Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
- Berechne die zugehörige Ober- und Untersumme.
- Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
| x | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| f(x) | 0 | 0,0625 | 0,25 | 0,5625 | 1 | 1,5625 | 2,25 | 3,0625 | 4 |
Für den Flächeninhalt der Obersumme gilt:
S = f (0,5) 0,5 + f (1) 0,5 + .....f (4) 0,5 = 0,5 f(0,5) + f(1) + ...f (4) = 6,375
Für den Flächeninhalt der Untersumme gilt:
s = f (0) 0,5 + f (0,5) 0,5 + .....f (3,5) 0,5 = 4,375
Mittelwert: 5,375
Gegeben ist die Funktion f(x) = 0.5 x².
- Zerlege das Intervall [0;1] mit dem Schieberegler in gleichlange Teilintervalle und bestimme die zugehörige Ober- und Untersumme mit dem Applet.

Das bestimmte Integral
- Informiere dich im
 Arbeitsblatt "Das bestimmte Integral" über die Definition des Begriffs "bestimmtes Integral".
Arbeitsblatt "Das bestimmte Integral" über die Definition des Begriffs "bestimmtes Integral". - Auf dem
 Arbeitsblatt sind für einige einfache Funktionen die bestimmten Integrale über dem Intervall [a;b] angegeben. Finde anschauliche Erklärungen für die Herleitung und berechne die bestimmten Integrale für die angegeben Werte!
Arbeitsblatt sind für einige einfache Funktionen die bestimmten Integrale über dem Intervall [a;b] angegeben. Finde anschauliche Erklärungen für die Herleitung und berechne die bestimmten Integrale für die angegeben Werte!  Lösung
Lösung - Berechne: ; ;
- Überprüfe die Lösung mit folgendem
 Applet, in dem du mit Hilfe der Schieberegler die Integrationsgrenzen anpasst!
Applet, in dem du mit Hilfe der Schieberegler die Integrationsgrenzen anpasst!
Flächenberechnung
- Erkläre den Unterschied zwischen dem Wert des bestimmten Integrals und dem Flächeninhalt zwischen Graph und x-Achse.
- Verwende dazu dieses Applet!
- Informiere dich im Video über Bestimmtes Integral, Flächenbilanz, Fläche über/unter der x-Achse.
Integralfunktion
- die Berechnung eines Integrals als Grenzwert von Unter- bzw. Obersumme ist aufwendig. Einfacher geht die Bestimmung mit der Integralfunktion.
- Betrachte im Applet die Integralfunktion
- Bearbeite als Zusammmenfassung das
 Arbeitsblatt "Die Integralfunktion"
Arbeitsblatt "Die Integralfunktion"

<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Einführung in die Integralrechnung,Mathematik,Einführung,Integralrechnung,12. Klasse,Oberstufe,Lernpfad</metakeywords>