Chaos und Fraktale
Dieser Lernpfad wurde für den Mathe-Tag an der Universität Würzburg entwickelt. Die Sieger der Fümo-Mathematik-Olympiade dürfen einen Tag an der Uni verbringen um gemeinsam mit Professoren und Lehrern unterhaltsame und interessante Themen der Mathematik zu entdecken.
Hinweis: Es empfiehlt sich die Links in einem neuem Fenster öffnen. Halte dazu die Shift-Taste gedrückt wenn du auf den Links klickst.
Kurs 1: Chaotische Bäume interaktiv
Informiere dich hier über die Begriffe Chaos und Fraktale.
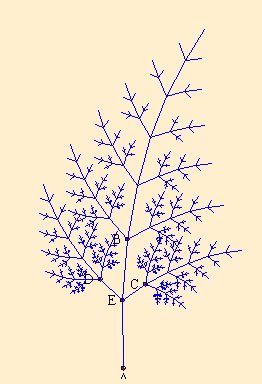
Fraktale sind also geometrische Formen, deren Struktur sich immer wieder - allerdings verkleinert - wiederholt. Vergrößert man umgekehrt Teile der Figur, so stößt man stets auf die gleiche Grundstruktur und dieses Vergrößern kann beliebig oft geschehen.
Pythagoras-Baum mit 60°-Winkel
Öffne das folgenes Applet in einem neuen Fenster und beantworte die folgenden Arbeitsaufträge:
- Durch mehrmaliges Klicken auf "Draw" entsteht eine Figur. Beschreibe diese Figur. Wie sieht sie aus?
- Lösche die Figur mit der Reset-Taste. Lasse nun nur die erste Stufe anzeigen. Aus welchen geometrischen Formen ist sie aufgebaut? Beschreibe diese möglichst genau! Wo ist der 60°-Winkel zu finden?
- Lasse die Figur jetzt Stufe für Stufe zeichnen und beschreibe jeweils, wie jede weitere Stufe aus der vorhergehenden entsteht.
- Woher kommt der Name Pythagorasbaum?
Pythagoras-Baum und verschiedene Winkel
Verändere nun in dem Applet auch den Winkel:
- Untersuche die Bäume für 10° und 80°. Welcher Zusammenhang besteht?
- Bei welchem Winkel wird der Baum achsensymmetrisch?
- Wie verändert sich das Aussehen der Bäume bei Winkeln zwischen 1° und 45°?
Spielen im pythagoräischen Garten
Durch ziehen am roten Punkt dieses Applets kannst du den Pythagorasbaum verändern. Findest du den Broccoli?
Farne
Es gibt auch Fraktale, die Ähnlichkeit mit einem Farn haben.
Eine Möglichkeit diese Pflanzen nachzubilden zeigt folgendes Applet.
Die Ausgangsfigur besteht hier jeweils aus Strecken.
Versuche durch Ziehen an den Endpunkten das folgende Bild zu erzeugen.
Weitere Informationen
Kurs 2: Drachenfalten einmal anders
Kurs 3: Dreimal Sierpinski
- Sierpinski Dreieck, Eckpunkte variierbar, bis Stufe 6
- Sierpinski Dreieck Stufen unbegrenzt
- Pascalsches Dreieck
- noch mehr Sierpinski
- Pascal und Sierpinski
Maria Eirich, Andrea Schellmann, 21.07.2006