Zylinder Pyramide Kegel/Zusatzaufgaben
Vorlage:Lernpfad Inhalt und Drumherum
Auf dieser Seite findest du zu jeder Lerneinheit (Zylinder, Satz von Cavalieri, Pyramide und Kegel) noch weitere Übungsaufgaben, mit denen du dein neu erworbenes Wissen festigen und weiter vertiefen kannst.
Die Bearbeitung der einzelnen Lerneinheiten und der darin enthaltenen Übungsaufgaben haben erste Priorität. Diese Zusatzaufgaben sind als freiwillige Übung gedacht und sollten daher außerhalb der Unterrichtszeit bearbeitet werden (außer du bist schon mit allen Lerneinheiten fertig).
Berechnungen am Zylinder
Bearbeite in deinem Schulbuch S.20 Nr.7 und Nr.8!
S.20 Nr.7:
Nr.7a)
Möglichkeit 1: a=U, b=h
Möglichkeit 2: b=U, a=h
Nr.7b)
"Zylinderausschnitte"
Tante Uschi hat für ihren Geburtstag eine Scharzwälderkirschtorte mit einem Durchmesser von 28cm und einer Höhe von 8cm gebacken. Die Torte kommt bei den Gästen so gut an, dass für sie selbst nur noch ein schmales Probierstück übrig bleibt, welches an der Spitze einen Winkel von 15° hat.
a) Wie viel Torte hat Tante Uschi bekommen (Volumen des Tortenstücks)?
Satz von Cavalieri
Wir betrachten zwei Quader, die die Kriterien von Cavalieri erfüllen (gleicher Grundflächeninhalt, gleiche Höhe, in gleicher Höhe gleichen Flächeninhalt der Schnittflächen). Der Grundflächeninhalt beträgt .
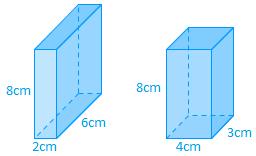
Der Oberflächeninhalt berechnet sich aus dem doppelten Grundflächeninhalt und dem Mantelflächeninhalt. Die Grundflächen unserer beiden Körper sind flächengleich. Wie sieht es aber mit den Mantelflächeninhalten aus?
Flächengleichheit bedeutet nicht, dass auch der Umfang gleich ist!
Im gewählten Beispiel wäre der Mantelflächeninhalt des linken Quaders und des rechten Quaders
Fazit: Der Satz von Cavalieri gilt nicht für den Oberflächeninhalt entsprechender Körper, da die Mantelflächen von verschiedenen Körpern nicht gleich groß sind, auch wenn Grundflächeninhalt und Höhe gleich sind!
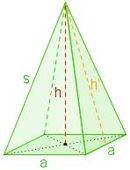
Berechnungen an der Pyramide
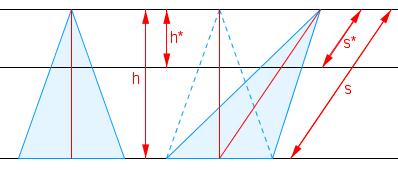
Für zwei gerade Pyramiden mit gleicher Höhe und gleich großer Grundfläche wurde die Volumengleichheit über die zentrische Streckung nachgewiesen. Bei der schiefen Pyramide wird ebenfalls die Grundfläche (in der Abbildung die Grundlinie) auf die Schnittfläche durch eine zentrische Streckung mit der Pyramidenspitze als Streckzentrum abgebildet. Für den Streckfaktor gilt (Strahlensatzfigur).
Es gilt für die Flächeninhalte der Schnittflächen: und
wegen