Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Efron

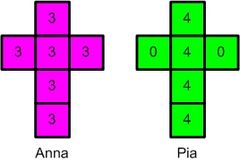
Die „Würfel von Efron“

Aufgabe

Findest du das Spiel fair?

Um dies herauszufinden, bastle dir die „Würfel von Efron“ ganz einfach nach. Nimm dazu beispielsweise vier helle Spielwürfel und beschrifte diese mit einem Folienstift so wie oben dargestellt, oder beklebe deine Würfel mit Papier. Jetzt spiele mit einem Freund oder einer Freundin nach den Spielregeln.

Wie ihr sicherlich herausgefunden habt, scheinen manche Würfel besser zu sein als andere. Wenn du die nächsten Aufgaben bearbeitest, wirst du erkennen, dass man mit einer gewissen Taktik sein Glück in diesem Spiel ganz schön beeinflussen kann.

Vorlage:Aufgaben-M

Eine mögliche Lösung ist zum Beispiel  $\Omega_{gruen} = \left\{ 4_1, 4_2, 4_3, 4_4, 0_1, 0_2 \right\}$  für den grünen Würfel.

Wichtig ist, dass  $\left|\Omega_{gruen}\right| = 6$  gilt.

Da jede Seite gleichwahrscheinlich ist, ist zum Beispiel die Wahrscheinlichkeit eine Null zu würfeln  $p\left(0\right)=\frac{2}{6}=\frac{1}{3}$   (siehe Definition der Laplace-Wahrscheinlichkeit).

Beispiel für eine falsche Lösung:   $\Omega = \left\{ 4, 0 \right\}\ .$  Hier sind die Ergebnisse nicht gleichwahrscheinlich!

Vorlage:Aufgaben-M

Lösungshinweise: Vorlage:Versteckt

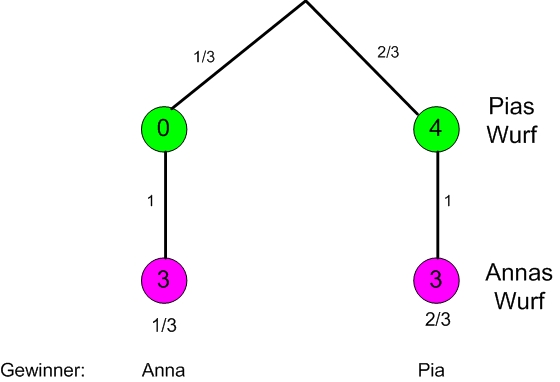
Da Anna sicher eine 3 würfelt, gewinnt sie nur wenn Pia eine 0 würfelt.

Nach Aufgabe 2 ist diese Wahrscheinlichkeit  $p\left(0\right)=\frac{1}{3}\ .$

Das Ereignis „Pia gewinnt“ ist das Gegenereignis dazu und berechnet sich demnach folgendermaßen:

$p(\mathrm{Pia\ gewinnt}) = 1 - \frac{1}{3} = \frac{2}{3}\ .$

Dies lässt sich aus dem folgenden Baumdiagramm erkennen:

Erklärung: 36-Felder-Tafel

Vorlage:Aufgaben-M

Tipp: Überlege dir alle Möglichkeiten mit zwei Würfeln gegeneinander zu spielen.

Für Interessierte: Vorlage:Aufgaben-M

Lösungshilfe: Vorlage:Versteckt

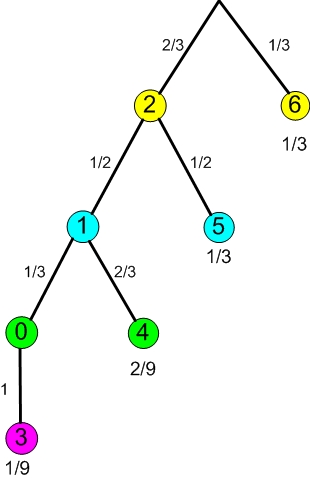
  Der gelbe Würfel gewinnt auf jeden Fall, falls er die 6 zeigt.
  Dann sind die anderen Würfel uninteressant.

  Falls er die 2 zeigt, muss der nächstbeste Würfel gesucht werden.

  Als nächstes kann der blaue Würfel gewinnen, falls er 5 zeigt.

  Wenn nicht, könnte der grüne Würfel gewinnen, falls er die 4 zeigt.

  Hat bis jetzt keiner gewonnen, gewinnt der rote Würfel.

Aufgabe

Spielt das Spiel zu viert nach! Würfelt mindestens zehnmal und vergleicht eure Gewinnstatistik mit den berechneten Wahrscheinlichkeiten.

---

Vorlage:Kasten Mathematik