Vera 8 interaktiv/Mathematik/Test B
Vorlage:Kurzinfo DSB/IQB Vorlage:Vera 8 Mathematik
Aufgabe 1.1: Rapido Aus der Preistabelle des Paketdienstes "Rapido" kann man zu jedem Paketgewicht den zugehörigen Preis ablesen:
Beantworte mit Hilfe der Tabelle folgende Frage. Wie viel kostet ein Paket, das 9 kg wiegt? Kreuze die richtige Lösung an. (!5,00 €) (6,00 €) (!9,00 €) (!13,50 €) | ||||||||||||||||||||||||||||||||||||
Aufgabe 1.2: Rapido Beantworte mit Hilfe der Tabelle aus 1.1 folgende Frage. Wie schwer darf ein Paket sein, für das man 5,00 € bezahlt? Kreuze die richtige Lösung an. (!Genau 4 kg) (!Höchstens 10 kg) (Über 3 kg bis 5 kg) (!Über 5 kg bis 8 kg) | ||||||||||||||||||||||||||||||||||||
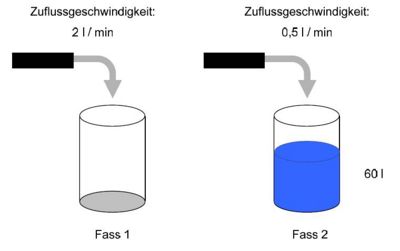
Aufgabe 2: Zwei Fässer Jedes der beiden dargestellten Fässer fasst genau 100l. Sie werden mit Wasser gefüllt. Zu Beginn des Füllvorgangs enthält Fass 2 bereits 60l. Fass 1 wird mit 2 l/min gleichmäßig gefüllt, Fass 2 mit 0,5 l/min. Stimmt es, dass Fass 2 zuerst überläuft? Schreib auf, wie du zu deiner Entscheidung gekommen bist.
Fass I : 2 x = 100
x = 50 => Fass I läuft nach 50 Min. über.
Fass II: 0,5 x + 60 = 100
x = 80 => Fass II läuft nach 80 Min. über. “
Fass I Fass II 30’ 60l 75l 31’ 62 32’ 64 76 33’ 66 34’ 68 77 35’ 70 36’ 72 78 37’ 74 38’ 76 79 39’ 78 40’ 80 80
Nach 80 Minuten, weil genau dann beide Fässer voll sind.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 3: Nachbarschaftshilfe Drei Schüler erledigen für einen kranken Nachbarn die Gartenarbeit. Fritz hat viel Zeit und fängt schon um 14 Uhr an zu arbeiten. Hans kommt um 15 Uhr und Max um 15:30 Uhr. Um 17 Uhr ist die Arbeit für alle drei erledigt. Der Nachbar gibt den Schülern 50,- € mit der Bitte, das Geld möglichst entsprechend der jeweils geleisteten Arbeitszeit zu verteilen. Wie viel Geld sollte jeder bekommen? Schreibe auf, wie du vorgehst.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 4.1: Verknüpfungen Für zwei Zahlen x und y soll gelten: x + y = 1. Kreuze die richtige Aussage an. (!Wenn x negativ ist, dann ist auch y negativ.) (!Wenn x größer ist als 1, dann ist auch y größer als 1.) (!Weder x noch y können negativ sein.) (Wenn x kleiner ist als 1, dann ist y positiv.) (!x und y müssen verschiedene Vorzeichen haben.)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 4.2: Verknüpfungen Für zwei Zahlen x und y soll gelten: x · y = 1. Kreuze die richtige Aussage an. (!Wenn x negativ ist, dann ist y positiv.) (!Wenn x größer ist als 1, dann ist auch y größer als 1.) (!Weder x noch y können negativ sein.) (!Wenn x kleiner ist als 1, dann ist y negativ.) (x und y müssen dasselbe Vorzeichen haben.)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 4.3: Verknüpfungen Für zwei Zahlen x und y soll gelten: . Kreuze die richtige Aussage an. (!Wenn x negativ ist, dann ist y positiv.) (Wenn x größer ist als 1, dann ist auch y größer als 1.) (!Weder x noch y können negativ sein.) (!Wenn x kleiner ist als 1, dann ist y negativ.) (!x und y müssen verschiedene Vorzeichen haben.) | ||||||||||||||||||||||||||||||||||||
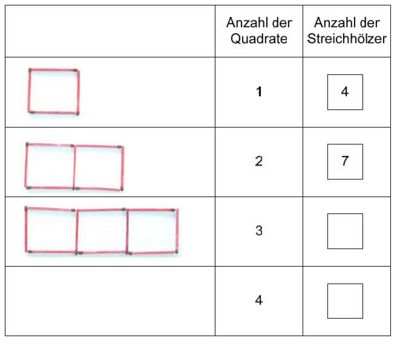
Aufgabe 5.2: Streichholzkette Wie viele Streichhölzer werden für 12 solche Quadrate benötigt? Kreuze die richtige Antwort an. (!23) (!24) (!36) (37) (!48)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 5.3: Streichholzkette Gib eine Gleichung an, die den Zusammenhang zwischen der Anzahl k der Quadrate und der Anzahl s der benötigten Streichhölzer allgemein beschreibt.
| ||||||||||||||||||||||||||||||||||||
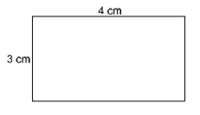
Aufgabe 6: Rechteck Ein Rechteck ist 4 cm lang und 3 cm breit. Wie groß ist sein Flächeninhalt? Kreuze an. (12cm2) (!7 cm) (!7 cm2) (!12 cm) (!14 cm)
| ||||||||||||||||||||||||||||||||||||
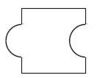
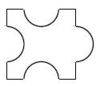
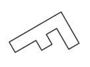
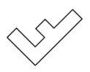
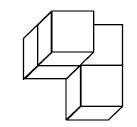
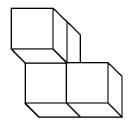
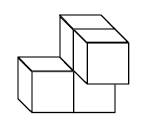
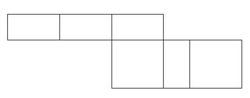
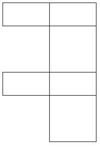
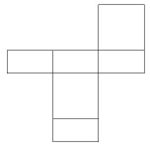
Aufgabe 7: Puzzleteile Welches dieser Puzzleteile hat den größten Flächeninhalt? Kreuze an.
| ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
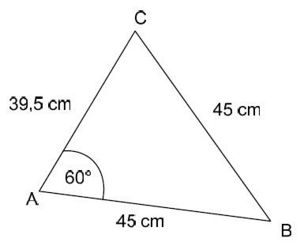
Aufgabe 9: Das unmögliche Dreieck Begründe, warum es kein Dreieck mit diesen Maßen geben kann.
| ||||||||||||||||||||||||||||||||||||
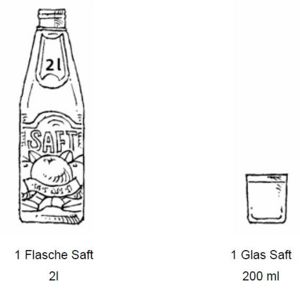
Aufgabe 10: Geld umrechnen Rechne um:
| ||||||||||||||||||||||||||||||||||||
Aufgabe 11: Minuten und Sekunden Rechne die Zeitangaben um und fülle die Lücken aus. Beispiel: 95 s = 1 min 35s
| ||||||||||||||||||||||||||||||||||||
Aufgabe 12: Fehlendes Zeichen Ordne zu:
| ||||||||||||||||||||||||||||||||||||
Aufgabe 13: Winkel im Dreieck In einem gleichschenkligen Dreieck ist der Winkel an der Spitze dreimal so groß wie ein Basiswinkel . Wie groß sind die Winkel dieses Dreiecks? Kreuze die richtige Antwort an. (!) (!) () (!)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 14: Nachbarseiten im Parallelogramm Bei einem Parallelogramm ist eine Seite 40 cm lang und eine banachbarte Seite 90 cm. Wie groß ist der Umfang des Parallelogramms? Kreuze an. (!130 cm) (!170 cm) (260 cm) (!340 cm) (!360 cm)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 15: Fahrplan Hier siehst du den Fahrplan von Köln mit dem Intervity IC 800 nach Hamburg.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 16: Fadenaufgabe Ein 34 Zentimeter langer Faden wird zu einem Rechteck gelegt. Die Breite des Rechteckes beträgt 8 Zentimeter. Wie lang ist das Rechteck? (!8 Zentimeter) (9 Zentimeter) (!13 Zentimeter) (!18 Zentimeter) | ||||||||||||||||||||||||||||||||||||
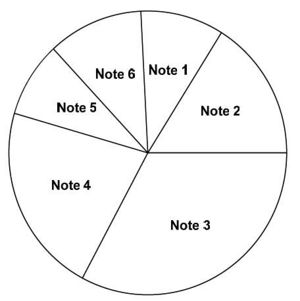
Aufgabe 17: Noten Das Kreisdiagramm zeigt die Notenverteilung einer Prüfung im Fach Englisch. Welche der folgenden Aussagen zu diesem Kreisdiagramm ist richtig? Kreuze an. (!Es gibt öfter die Note 2 als die Note 4.) (!Ein Drittel der Schülerinnen und Schüler hat die Note 1 oder die Note 2.) (Mehr als 50% der Schülerinnen und Schüler haben eine bessere Note als die Note 4.) (!Weniger als ein Viertel der Schülerinnen und Schüler haben die Note 3.) | ||||||||||||||||||||||||||||||||||||
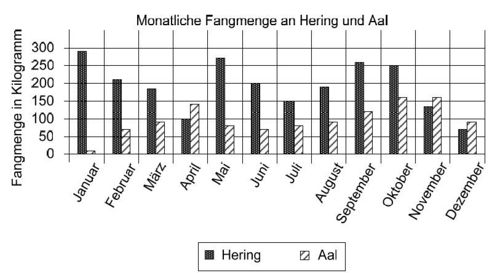
Aufgabe 18: Fisch Das Diagramm zeigt die Menge gefangenen Fischs in jedem Monat. In welchem Zeitraum ist die monatliche Fangmenge an Aal im Vergleich zum Vormonat laut Diagramm prozentual am meisten angestiegen? Kreuze an. (!von März nach April) (!von April nach Mai) (!von September nach Oktober) (von Januar nach Februar) | ||||||||||||||||||||||||||||||||||||
Aufgabe 19: Schultaschen Die Schülerinnen und Schüler der Klasse 5a sitzen in Tischgruppen zu jeweils 5 oder 6 Schülerinnen und Schülern. Heute werden im Unterricht die Schultaschen gewogen. Paul kommt zu spät. Die anderen aus seiner Tischgruppe haben bis dahin schon ihre Taschen gewogen: 3,7 kg, 4,6 kg, 4,8 kg, 5,2 kg, 5,3 kg. Mit Pauls Schultasche ergibt sich in dieser Tischgruppe ein druchschnittliches Gewicht von 4,9 kg. Welches Gewicht hatte Pauls Schultasche?
| ||||||||||||||||||||||||||||||||||||
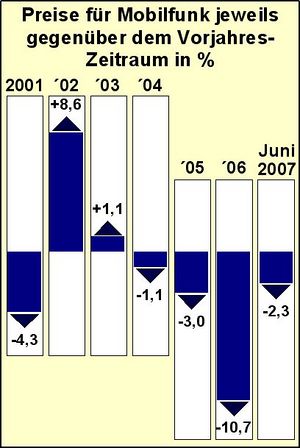
Aufgabe 20.1: Preisänderungen im Mobilfunk In dem Diagramm wird dargestellt, wie sich die Preise für Mobilfunk im Vergleich zum Vorjahr prozentual geändert haben. Zum Beispiel sind 2002 die Preise im Vergleich zu 2001 um 8,6 % angestiegen, während die Preise im Vergleich zu 2005 um 10,7 % gefallen sind.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 20.2: Preisänderungen im Mobilfunk Um wie viel Prozent sind die Preise von 2002 gegenüber den Preisen von 2000 gestiegen? Kreuze an. (ca. 3,9 %) (!ca. 4,3 %) (!ca 8,6 %) (!ca. 12,9 %)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 20.3: Preisänderungen im Mobilfunk Marvin behauptet: "2004 waren die Preise genauso hoch wie 2002." Julia sagt: "Nein, sie waren niedriger." Wer von beiden hat recht? Begründe deine Entscheidung.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 21: Gelbgrüner Würfel Jede der sechs Flächen eines Würfels ist entweder gelb oder grün angestrichen. Beim Würfeln ist die Wahrscheinlichkeit , dass gelb oben liegt. Kreuze an, wie viele Flächen grün sind. (!eine) (!zwei) (!drei) (vier) (!fünf) | ||||||||||||||||||||||||||||||||||||
Aufgabe 22: Der sechste Wurf Ein normaler Spielwürfel wird geworfen. In fünf aufeinander folgenden Würfen landet der Würfel jedes Mal so, dass eine gerade Zahl angezeigt wird. Nun wird der Würfel ein sechstes Mal geworfen. Welche der folgenden Aussagen triftt dann zu? Kreuze an. (!Es ist wahrscheinlicher, dass der Würfel eine gerade Zahl zeigt, als dass er eine ungerade Zahl zeigt.) (!Es ist wahrscheinlicher, dass der Würfel eine ungerade Zahl zeigt, als dass er eine gerade Zahl zeigt.) (Es ist gleich wahrscheinlich, dass eine gerade Zahl oder eine ungerade Zahl gezeigt wird.) (!Der Würfel zeigt mit Sicherheit eine ungerade Zahl.) | ||||||||||||||||||||||||||||||||||||
Aufgabe 23: Schrauben In einer Firma, in der Schrauben hergestellt werden, wird am Ende des Produktionsprozesses eine Endkontrolle durchgeführt. Eine überprüfte Kiste enthält 10000 Schrauben. Aus dieser Kiste werden zufällig 200 Schrauben ausgewählt ud überprüft. 10 dieser Schrauben lagen außerhalb der Norm. Wie viel Schrauben, die nicht der Norm entsprechen, sind ungefähr in der ganzen Kiste enthalten? Kreuze an. (!20) (!50) (!200) (500) (! 2000) | ||||||||||||||||||||||||||||||||||||
Aufgabe 24.1: Temperatur In dieser Tabelle stehen Temperaturangaben, die jeweils zu festen Uhrzeiten gemessen wurden.
Wann wurde die niedrigste Temperatur gemessen? Kreuze alle richtigen Antworten an. (!Donnerstag um 9 Uhr) (Montag um 6 Uhr) (!Mittwoch um 15 Uhr) (Donnerstag um 21 Uhr) (!Dienstag um 6 Uhr) | ||||||||||||||||||||||||||||||||||||
Aufgabe 24.2: Temperatur Welcher Tag war der wärmste? Begründe deine Entscheidung mit den Temperaturangaben aus der Tabelle von 24.1.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 25: Internetnutzung 56% der Internetnutzer sind täglich oder fast täglich online Die Nutzung des Internets hat in Deutschland weiter zugenommen. Fast zwei Drittel der Personen ab zehn Jahren (65%) nutzten im ersten Quartal 2006 das Internet. Dies geht aus der aktuellen Auswertung der Befragung privater Haushalte zur Nutzung von Informations- und Kommunikationtechnologien hervor. [...] Innerhalb der Gruppe der Internetnutzer ging im ersten Quartal 2006 mehr als die Hälfte (56%) täglich oder fast täglich online, ein Jahr zuvor waren es noch 50% der Internetnutzer. (Statistisches Bundesamt) Welcher Prozentsatz der Personen ab 10 Jahren ging damit im ersten Quartal 2006 täglich oder fast täglich online? Kreuze an, welcher Wert deinem Ergebnis am nächsten liegt. (36%) (!56%) (!65%) (!86%) (!121%)
| ||||||||||||||||||||||||||||||||||||
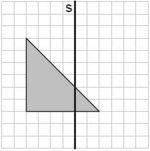
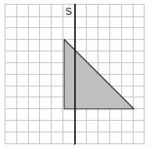
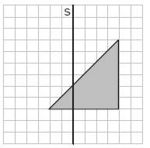
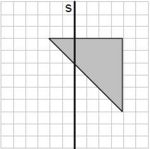
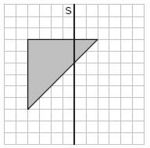
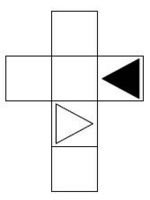
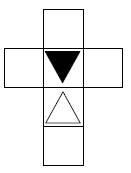
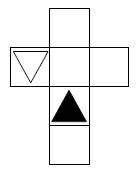
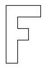
Aufgabe 27: Spiegelung
Das graue Dreieck wird an der Achse a gespiegelt. Welche der Figuren stellt das Ergebnis der Spiegelung dar? Kreuze an.
| ||||||||||||||||||||||||||||||||||||
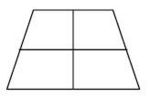
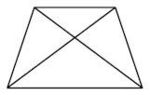
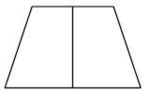
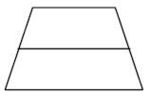
Aufgabe 29: Symmetrieachsen im Trapez Welche Zeichnung zeigt alle Symmetrieachsen eines gleichschenkligen (symmetrischen) Trapezes? Kreuze an.
| ||||||||||||||||||||||||||||||||||||
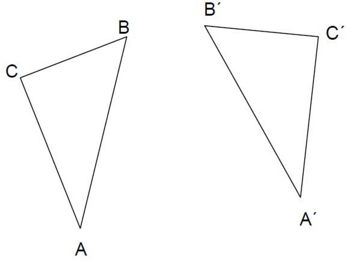
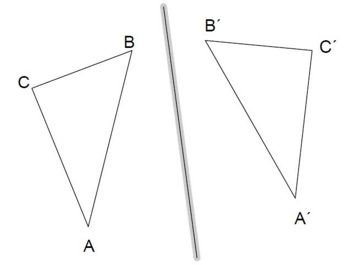
Aufgabe 30: Spiegelachse Das Dreieck A'B'C' ist das Ergebnis einer Achsenspiegelung des Dreiecks ABC. Zeichne die Spiegelachse g ein.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 31: Parallelogramme Welche dieser Aussagen, die für alle Parallelogramme gelten sollen, ist FALSCH? Kreuze an. (!Gegenüberliegende Seiten sind parallel.) (!Die Diagonalen halbieren sich gegenseitig.) (!Gegenüberliegende Winkel sind gleich groß.) (Es gibt genau eine Spiegelachse.) (!Gegenüberliegende Seiten sind gleich lang.)
| ||||||||||||||||||||||||||||||||||||
Aufgabe 36: Gleichschenklige Dreiecke Sind folgende Aussagen wahr oder falsch? Jedes gleichschenklige Dreieck ...
| ||||||||||||||||||||||||||||||||||||
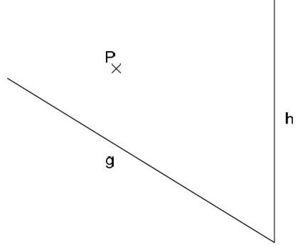
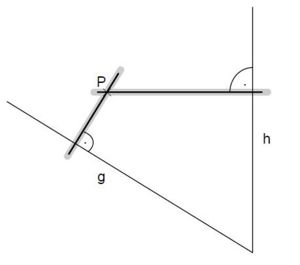
Aufgabe 37: Punkte und Abstände Gegeben sind zwei Halbgeraden g und h und ein Punkt P. Zeichne eine Senkrechte durch den Punkt P auf die Halbgerade g und eine Senkrechte durch den Punkt P auf die Halbgerade h.
| ||||||||||||||||||||||||||||||||||||
Aufgabe 38: Dreieck In einem gleichschenkligen Dreieck ist die Basis doppelt so lang wie die Höhe. Wie groß sind die Winkel dieses Dreiecks?
|