Einführung in die Differentialrechnung

Vorlage:Lernpfad-M

Einstiegsaufgabe 1 - Blumenvase

Vorlage:Mathematik
{{Experiment| Skizzieren Sie zunächst einen möglichen Verlauf des Füllgraphen für die Gefäße in ein Koordinatensystem. Verlgeichen Sie ihre Ergebnisse mit einer anderen Zweiergruppe und begründen ihre Skizze.

Mit dem folgenden Experiment können Sie ihre Vermutung aus der ersten Aufgabe überprüfen. Dazu sollen Sie gleichmäßig Wasser in ein Gefäß füllen. Mit einer Stoppuhr wird die Zeit gemessen, wie lange der Wasserspiegel braucht um auf 0.5 cm, 1 cm, 1.5 cm, 2cm usw. zu steigen. Die Messdaten für die Zeit übertragen Sie danach vom Arbeitsblatt in die untenstehende GeoGebra-Tabelle.

<popup name="Versuchsaufbau"> Vorlage:Kasten blau

Vorlage:Aufgaben-M

Einstiegsaufgabe 2 - Barringer-Krater

Die Idee zu dieser Aufgabe entstammt dem Schulbuch Lambacher-Schweizer, Analysis Leistungskurs Gesamtband, Ausgabe A, Klett Verlag, Stuttgart 2001, ISBN 3127321805. Vorlage:Mathematik

Vorlage:Aufgaben-M

Von der mittleren zur momentanen Änderungsrate

Blumenvase

In der Einstiegsaufgabe haben Sie in Gefäßen gleichmäßig Wasser eingelassen und die Höhe des Wasserstandes gemessen. Betrachten wir nun die abgebildete Vase, in die ebenfalls gleichmäßig Wasser eingelassen wird. Die Tabelle stellt dar, wie sich die Wasserhöhe (hier gemessen vom Tischboden) in der Vase beim Einfüllvorgang im Zeitverlauf verändert. Im Gegensatz zum Vorgehen zur Einstiegsaufgabe wurde nun alle drei Sekunden die Höhe des Wasserstandes gemessen.

Zeit (Sekunden)	Höhe (cm)
0	0,51
3	1,33
6	2,74
9	4,91
12	8,00
15	12,17
18	17,58

Die mittlere Änderungsrate gibt an, wie viel Zentimeter pro Sekunde die Wasserhöhe in einem Zeitabschnitt im Schnitt zunimmt.

Bsp.
In den drei Sekunden zwischen Sekunde 6 und 9 steigt das Wasser um 4,91 cm - 2,74 cm = 2,17 cm. Daher nimmt das Wasser pro Sekunde um 2,17 cm : 3 s = 0,72 cm/s zu. Die mittlere Änderungsrate im Zeitabschnitt von Sekunde 6 und Sekunde 9 beträgt daher 0,72 cm pro Sekunde (abgekürzte Schreibweise: 0,72 cm/s)

<popup name="Lösung"> a) In den ersten drei Sekunden steigt die Wasserhöhe um 1,33 cm - 0,51 cm = 0,82 cm. Pro Sekunde steigt es daher um 0,82 cm : 3 s = 0,273 cm/s.
b) In den drei Sekunden von Sekunde 3 auf Sekunde 6 nimmt die Wasserhöhe um 2,74 cm - 1,33 cm = 1,41 cm zu. Die mittlere Änderungsrate ist daher 1,41 cm : 3 s = 0,47 cm/s.
c) Zwischen Sekunde 12 und 15 liegen wiederum 3 Sekunden. In diesem Zeitraum steigt das Wasser um 12,17 cm - 8 cm = 4,17 cm. Pro Sekunde nimmt das Wasser in diesem Zeitraum daher um 4,17 cm : 3 s = 1,39 cm/s zu.
d) Bei Sekunde 3 beträgt die Wasserhöhe 1,33 cm, während sie bei Sekunde 12 genau 8 cm beträgt. In diesen 9 Sekunden ist die Wasserhöhe also um 8 cm - 1,33 cm = 6,67 cm gesteigen. Die mittlere Änderungsrate zwischen Sekunde 3 und 12 beträgt daher 6,67 cm : 9 s = 0,741 cm/s.
e) Das Wasser nimmt in den ersten 18 Sekunden um 17,58 cm - 0,51 cm = 17,07 cm zu. Die mittlere Änderungsrate beträgt in diesem Zeitintervall daher 17,07 cm : 18 s = 0,948 cm/s.
</popup>

Vorlage:Mathematik
Vorlage:Aufgaben-M

<popup name="Applet">

</popup>

<popup name="Lösung"> a) Bei Sekunde 12 beträgt die Wasserhöhe genau 8 cm, während das Wasser bei Sekunde 13 die Höhe 9,261 cm hat. In der einen Sekunden ist es also um 9,261 - 8 cm = 1,261 cm gestiegen. Die mittlere Änderungsrate in diesem Zeitabschnitt beträgt daher 1,261 cm/s.
b) 8,6151 cm - 8 cm = 0,6151 cm => 0,6151 cm : 0,5 s = 1,2302 cm/s
c) 1,206 cm/s
d) 1,204 cm/s
e) Der Wert scheint gegen 1,2 cm/s zu streben.
</popup>

Vorlage:Aufgaben-M <popup name="Lösung"> a)
$w(12)=0,001(12+8)^3=8$
$w(12,001)=0,001(12,001+8)^3=8,00120006$
=> Höhenzunahme: $8,00120006 cm - 8 cm = 0,00120006 cm$
=> mittlere Änderungsrate: $0,00120006 cm : 0,001 s = 1,20006 cm/s$
b) Der Zeitabschnitt für die mittlere Änderungsrate müsste immer kleiner gewählt werden, z.B. zwischen Sekunde 12 und 12,00001 usw.
</popup>

Von der Sekanten- zur Tangentensteigung

Barringer-Krater

Vorlage:Mathematik

Vorlage:Aufgaben-M

<popup name="Applet">

</popup>
<popup name="Lösung">

</popup>

Vorlage:Aufgaben-M <popup name="Lösung"> $m=\frac{320-180}{400-300}=\frac{140}{100}=1,4$

Dieser Wert ist größer als 1,15. Das heißt, dass das Raumfahrzeug diese Steigung nicht mehr bewältigen kann. Es ist aber auch nur die durchschnittliche Steigung zwischen den Punkten A und B und nicht die Steigung im Punkt A, die für das Herauskommen des Fahrzeugs interessant ist. </popup>

Vorlage:Kasten blau

In der Graphik der Lösung der Aufgabe 6 kann man den Punkt B bewegen, indem man mit der Maus auf ihn zeigt und bei gedrückter linker Maustaste die Maus bewegt.

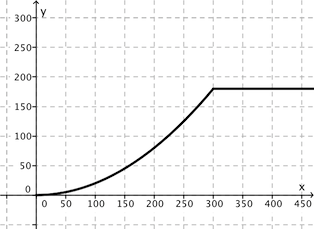
Um zu entscheiden, ob das Fahrzeug aus dem Krater heraus kommt, muss ein genauer Wert für die Steigung der Tangenten an den Graphen im Punkt A betrachtet werden. Wenn die Steigung des Kraters im Punkt A(300|180) kleiner als 1,15 ist, kann das Raumfahrzeug den Krater verlassen.

Die weiteren Betrachtungen führen wir nun etwas allgemeiner auch für andere Funktionen durch, bevor wir die Steigung im Punkt A des Kraters tatsächlich berechnen.

Verallgemeinerung

Die Überlegungen, die wir für die Kraterfunktion angestellt haben, kann man auch für andere Funktionen durchführen.

<popup name="Lösung"> a) Die Steigung ist (ungefähr) 3.
b) Die Steigung ist (ungefähr) 2,5.
c) Die Steigung ist (ungefähr) 2. </popup>

<popup name="Lösung"> a) Die Steigung ist $m=\frac{4-1}{2-1}=3$.
b) Wählt man $x_1=1,5$, so ergibt sich $m=2,5$.
c) Wenn man x₁ sehr dicht an 1 wählt, ist die Näherung recht genau. Vorlage:Kasten blau </popup>

Vorlage:Mathematik

<popup name="Applet">

</popup>

<popup name="Lösung">

Vorlage:Untersuchen Vollziehen sie im Applet den Übergang von der Sekante zur Tangente nach. Wie ändert sich dabei h?

Sekantensteigung: $m=\frac{f(x_0+h)-f(x_0)}{h}$

Wenn man h= 0 setzt, würde man durch 0 dividieren, was ja nicht erlaubt ist. Daher können wir zur Bestimmung der Tangensteigung nicht einfach h gleich 0 setzen, sondern können nur einen Grenzwert betrachten, indem wir h immer kleiner werden lassen und so der 0 annähern. </popup>

Vorlage:Aufgaben-M
<popup name="Lösung"> Die Sekantensteigung ist $m=\frac{(1+h)^2-1^2}{h}=\frac{(1+0,1^n)^2-1}{0,1^n}$. Dies muss für verschiedene n ausgerechnet werden. (Bei der Tabellenfunktion des Taschenrechners muss statt n als Variable x gewählt werden.)

n	h	x1	Sekantensteigung m
0	1	2	3
1	0,1	1,1	2,1
2	0,01	1,01	2,01
3	0,001	1,001	2,001
4	0,0001	1,0001	2,0001
5	0,00001	1,00001	2,00001

</popup>
Vorlage:Differenzieren Vorlage:Aufgaben-M

<popup name="Lösung"> a) Die Steigung ist 6.
b) Die Steigung ist 12. </popup>

Differenzenquotient

Vorlage:Aufgaben-M
Plenumsphase

Differentialquotient

Der Differentialquotient f'(x₀ )

• beschreibt die momentane Änderungsrate der Funktion f an der Stelle x₀ und entsteht im Rahmen eines Grenzprozesses, wenn man bei der durchschnittlichen Änderungsrate zwischen x₀ und x₁ den Wert x₁ immer mehr dem Wert x₀ annnährt,
• beschreibt die Steigung der Tangenten an den Graphen der Funktion im Punkt A(x₀|f(x₀)) und entsteht, wenn man in Rahmen eines Grenzprozesses bei der Sekantensteigung zwischen den Punkten A(x₀|f(x₀)) und B(x₁|f(x₁)) den Punkt B(x₁|f(x₁)) immer mehr dem Punkt A(x₀|f(x₀)) annähert.

<popup name="Applet">

</popup>

Vorlage:Protokollieren Schreiben Sie die Definition des Differentialquotienten zusammen mit einer Skizze in Ihr Heft.

Andere Schreibweise des Differentialquotienten:

Statt den Wert x₁ immer mehr dem Wert x₀ anzunähern, können wir auch jetzt wieder die Differenz der beiden Werte $h=x_1-x_0$ immer kleiner werden lassen.

Vorlage:Aufgaben-M <popup name="Lösung"> $f'(x_0)=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}$

Dies nennt man die h-Schreibweise des Differentialquotienten.

Vorlage:Untersuchen Vergleichen Sie die beiden Applets und untersuchen Sie die Veränderungen. </popup>

Mit Hilfe dieser h-Schreibweise des Differentialquotienten kann man die Ableitung f'(x₀) berechnen.

Vorlage:Aufgaben-M

Ableitungsfunktion

Beispielaufgabe:
Betrachtet wird die Funktion $k(x)=0,002x^2$ (die in der Einstiegsaufgabe die Höhes des Kraters beschreibt).

• Die Ableitung an der Stelle x=100 wird wie folgt berechnet:

<popup name="Lösung">

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle f'(100)= \lim_{h\to\0} \frac{f(100+h)-f(100)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (100+h)^2-0,002 \cdot 100^2}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (100^2+2 \cdot 100h+h^2-100^2)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (2 \cdot 100h+h^2)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} 0,002 \cdot \left( 2 \cdot 100+h \right)=0,004 \cdot 100 = 0,4}

</popup>

• Ganz analog lässt sich die Ableitung auch für eine beliebige Stelle x=x₀ bestimmen:

<popup name="Lösung">

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle f'(x_0)= \lim_{h\to\0} \frac{f(x_0+h)-f(x_0)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (x_0+h)^2-0,002 \cdot x_0^2}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (x_0^2+2 \cdot x_0 \cdot h+h^2-x_0^2)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} \frac{0,002 \cdot (2 \cdot x_0 \cdot h+h^2)}{h}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle = \lim_{h\to\0} 0,002 \cdot \left( 2 \cdot x_0+h \right)=0,004 \cdot x_0}

</popup>

Vorlage:Aufgaben-M

Vorlage:Mathematik

Vorlage:Aufgaben-M
<popup name="Applet">

</popup>

Diagnoseinstrument