Zusammenhang zwischen Graph einer Funktion und Ableitung

Lernpfad

Im folgenden Lernpfad werden Tangente und Normal an einem Funktionsgraphen graphisch veranschaulicht. Er wurde für Schülerinnen und Schüler konzipiert, die bisher noch keinerlei Erfahrungen im Umgang mit einem dynamischen Geometrieprogramm gesammelt haben.

Ziele:

• Zusammenhang zwischen dem Graphen einer Funktion und deren Ableitung
• Zeichnen von Funktionsgraphen
• graphische Bestimmung von waagrechten Tangenten

Material:

 Arbeitsblatt

Graph einer Funktion und die Tangente

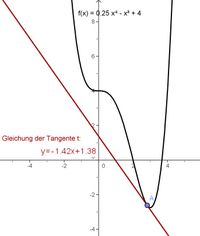
Zur genauen Analyse und zum Erkennen des Zusammenhangs zwischen dem Graph der Funktion und deren Ableitung ist es sinnvoll, die Tangenten an verschiedenen Punkten des Graphen näher zu untersuchen.

Aufgabe 1

1. Betrachte den Graph der Funktion f(x)= 0,25x⁴- x³ + 4. Durch Verschieben des Punktes A auf dem Graphen der Funktion erkennst Du, wie sich die Tangente dem Verlauf des Graphen der Funktion jeweils anpasst. (Alternativ kannst Du durch Anklicken des Punktes A diesen aktivieren und mit den Pfeiltasten ihn entlang des Graphen wandern lassen.) An welchen Punkten besitzt die Tangente eine positive, wann eine negative Steigung? Wann ist die Steigung der Tangenten gleich Null?
2. An welchen Punkten besitzt der Graph der Funktion waagrechte Tangenten? Zeichne auf Deinem Arbeitsblatt farbig alle waagrechten Tangenten ein!
3. Welcher Zusammenhang besteht zwischen der Steigung der Tangenten und der Steigung der Funktion in einem bestimmten Punkt?

Graph einer Funktion und die Ableitung

Welcher Zusammenhang besteht zwischen der Funktion und deren Ableitung?

Aufgabe 1

1. Durch Ziehen des Punktes A entlang des Funktionsgraphen zeichnet sich der Graph der Ableitung
2. Bestimme die Funktionsgleichung der Ableitung der Funktion und notiere diese auf dem Arbeitsblatt!
3. Ergänze den Zusammenhang zwischen dem Graph einer Funktion und dessen Ableitung auf Deinem Arbeitsblatt

Vergleiche weitere Graphen von Funktionen mit dem entsprechenden Graph der Ableitung

Betrachte den Graph der Funktion f mit der Funktionsgleichung f(x)=sin(x)

1. Zeichne den Graph der Funktion f in Geogebra
2. Zeichne an einen beliebigen Punkt eine Tangente an den Graph der Funktion. (Blende sie im Anschluss wieder aus)
3. Zeichen alle waagrechten Tangenten ein! (Blende sie im Anschluss wieder aus)
4. Zeichne den Graph der Ableitung von f! (Ableitung[f])
5. Wähle einen Punkt auf den Graphen und den entsprechenden Punkt auf dem Graph der Ableitung. Lass diesen entlang der Funktion wandern und vergleiche!

Vergleiche analog nacheinander den Graph der Funktion mit dem Graph der Ableitung:

1. g(x) = -$x^4+x^3$
2. h(x) = $(x^3-3)/x$

Ableitungspuzzles

In den nächsten Applets sollen vorgegebene Funktionsgraphen - in Form von Puzzles - so plaziert werden, daß unterhalb des Graphen jeder Funktion der Graph ihrer Ableitung steht. Bei Nicht-Gelingen erscheint auf Wunsch ein Text, der begründet, warum die getroffene Plazierung nicht richtig sein kann. Die Applets sollen das Verständnis des Differenzierens als Übergang von einer Funktion zu einer anderen festigen.

1. Öffne das Ableitungs-Puzzle 1 und platziere den Graph der jeweiligen Ableitung unter den entsprechenden Graph der Funktion!Achtung: Es handelt sich hier um eine Flash-Animation, die eventuell von deinem Browser nicht angezeigt wird.
2. Für besonders Schnelle: Schwieriger wird es beim Lösen des Ableitungs-Puzzles 2 und 3, da dieses auch Asymptoten und Singularitäten enthält... Probiere es aus! Achtung: Es handelt sich hier um eine Flash-Animation, die eventuell von deinem Browser nicht angezeigt wird.
3. Ordne im folgenden Ableitungspuzzle den entsprechenden Graphen den Graph der jeweiligen Ableitung zu!