Integralrechnung

Lernpfad

Im folgenden Lernpfad soll eine Einführung in die Integralrechnung mit den wichtigsten Grundlagen sowohl für Grund- als auch Leistungskurse in Mathematik der Jahrgangsstufe 12 gegeben werden.

Der Lernpfad wurde im Rahmen der schriftlichen Hausarbeit zur zweiten Staatsprüfung für das Lehramt an Gymnasien und Gesamtschulen von Daniel Jacobs (Benutzername: Dickesen) erstellt und im Unterricht der Jahrgangsstufe 12 eingesetzt.

Hinweise:

Du kannst Dir jederzeit die Lösungen der Aufgaben zeigen lassen die Du gerade bearbeitest, obwohl ich selbstverständlich erst nach eigenständiger Bearbeitung dazu rate!
Zusätzlich enthalten einige Aufgaben Tipps zur Lösung. Du kannst sie benutzen, falls Du an einem Punkt nicht weiterkommst.
Du solltest in jedem Fall alle Aufgaben im Heft schriftlich mit Angabe des Lernpfades (www-Adresse und Überschrift!) bearbeiten sowie alle Definitionen, Ideen, etc. ebenfalls schriftlich übernehmen!

So, jetzt geht's aber los! Zunächst etwas zum Aufwärmen, Fokussieren und Eingewöhnen:

Einführendes Beispiel

Aufgabe 1

Ein Hund rennt im Garten am Zaun hin und her und jagt die Passanten. Das Diagramm zeigt die Geschwindigkeit $v$ des Hundes, wobei positives $v$ die Bewegung nach rechts, negatives $v$ die Bewegung nach links bedeutet. Die Geschwindigkeit $v$ wird dabei in Meter pro Sekunde (m/s), die Zeit $t$ in Sekunden (s) gemessen.

Der Hund startet zur Zeit t = 0 in der Mitte des Zauns.



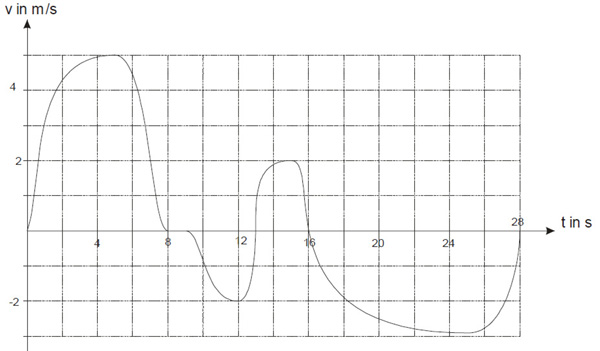
Bearbeite die folgenden Aufgaben und begründe Deine Antwort anhand des Graphen:

a) In welchen Zeitabschnitten bewegt sich der Hund nach rechts bzw. nach links?

Vorlage:Lösung

b) Wann hat der Hund die größte Geschwindigkeit nach rechts bzw. nach links erreicht?

Vorlage:Lösung

c) Wann wird der Hund schneller, wann wird er langsamer?

Vorlage:Lösung

d) Gib eine Schätzung für die Breite des Grundstücks an unter der Voraussetzung, dass der Hund zum Zeitpunkt t = 8 die Grundstücksgrenze erreicht hat.

Vorlage:Lösung

e) Im letzten Aufgabenteil hast Du ausgehend von der vom Hund zurückgelegten Strecke die Grundstücksbreite geschätzt. Woran kann man die zurückgelegte Strecke in obigem Diagramm erkennen?

Vorlage:Lösung

f) Befindet sich der Hund nach 28 Sekunden rechts oder links von der Mitte des Zauns?

Vorlage:Lösung

>>Weiter>>

Vorlage:Navigation Lernpfad Integral

<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Integral,Mathematik,12. Klasse,Oberstufe,Lernpfad</metakeywords>