Trigonometrische Funktionen/Einfluss von a

FAQ

Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.

Einfluss von a

Wir betrachten nun den Einfluss von $\ a$ in

$x \rightarrow a\cdot \sin x$.

Aufgabe A1

Die Datei [INVALID] wurde nicht gefunden.

1. Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von $\ a$ ändern.
   
2. Stelle den Schieberegler auf $\ a = 2$ ein. Wie ändert sich der Graph?
   
3. Überlege dir, wie sich die Werte $\ a = 3$ und $\ a = -1$ sowie $\ a = 0,5$ auf den Graphen auswirken und überprüfe deine Vermutung.
   
4. Formuliere das Ergebnis deiner Untersuchungen.

Merke

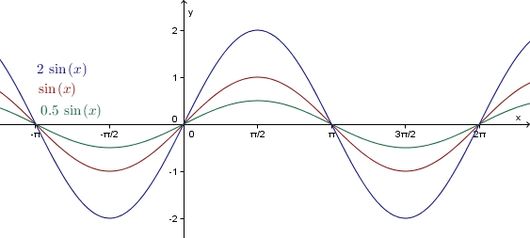
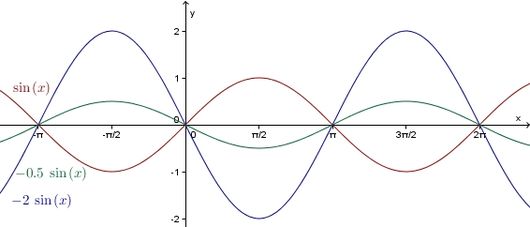
Man erhält den Graph der Funktion

$x \rightarrow a\cdot \sin x$

aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der $\ y$-Achse. Genauer:

• Ist der Betrag von $\ a$ größer als eins, so wird der Graph der Sinusfunktion in $\ y$-Richtung mit dem Faktor Betrag von $\ a$ gestreckt.
• Ist der Betrag von $\ a$ kleiner als eins, so wird der Graph der Sinusfunktion in $\ y$-Richtung mit dem Faktor Betrag von $\ a$ gestaucht.
• Falls $\ a$ negativ ist, so wird der Graph zusätzlich an der $\ x$-Achse gespiegelt.

Der Betrag von $\ a$ wird auch als Amplitude bezeichnet.

Aufgabe A2

Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen!

Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig.

Eine mögliche formale Begründung:

$a\cdot \sin x = 0$ mit $a\neq 0$

$\Leftrightarrow \sin x = 0$

d.h. die Nullstellen bleiben gleich. Ferner wird jeder Funktionswert mit dem gleichen Faktor multipliziert. Ist der Betrag dieses Faktors größer als 1, so wird der Graph in Richtung der y-Achse um diesen Faktor gestreckt, ist er kleiner als 1, so wird er entsprechend gestaucht. Ist der Faktor negativ, so wird der Graph zusätzlich an der x-Achse gespiegelt.

Aufgabe A3

Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen!

$\ a<-1;$	$-1<\ a<0;$	$0<\ a<1;$	$1<\ a$
				Verschiebung nach oben
				Verschiebung nach unten
				Verschiebung nach rechts
				Verschiebung nach links
				Streckung in $\ x$- Richtung / Verkleinerung der Frequenz
				Stauchung in $\ x$- Richtung / Vergrößerung der Frequenz
				Streckung in $\ y$- Richtung / Vergrößerung der Amplitude
				Stauchung in $\ y$- Richtung / Verkleinerung der Amplitude
				Spiegelung an $\ x$- Achse

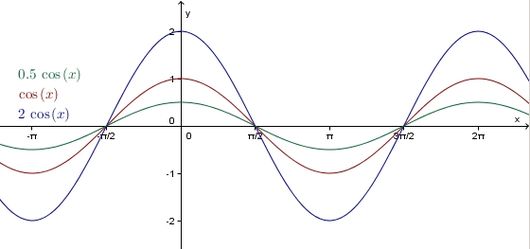
Nun betrachten wir den Einfluss von $\ a$ in

$x \rightarrow a\cdot \cos x$.

Aufgabe A4

Die Datei [INVALID] wurde nicht gefunden.

Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe A1 noch einmal für $cos$.

Die allgemeine Kosinusfunktion verhält sich bei Variation von $\ a$ genauso wie die allgemeine Sinusfunktion.

---

Hefteintrag: Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist!

---

Zurück zu Station 1: Einfluss der Parameter