Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als Steigung der Tangente

Die Tangente

Sie hatten bereits in der Sekundarstufe 1 mit Tangenten zu tun und haben diese im Zusammenhang mit kreisen kennengelernt.

Aufgabe 1

a) In diesem Applet sehen Sie zwei verschiedene Tangenten. Nennen Sie Unterschiede und Gemeinsamkeiten der beiden Tangenten

Text zum Verstecken

b) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie was Sie sehen.

Text zum Verstecken

c) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie was Sie sehen.

Merksatz

d) Ergänzen Sie zu den Gemeinsamkeiten aus Aufgabe a) was Ihnen in Aufgabe b) und c) aufgefallen ist.

Die Tangente als Schmiegegerade

Die Eigenschaft der Tangente sich dem Graphen einer Funktion in einer kleinen Umgebungen anzupassen bezeichnet als die ,,Schmiegeeigenschaft" der Tangente

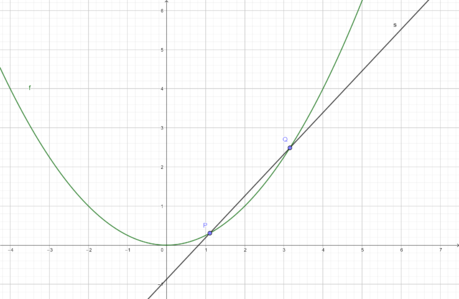
Die Steigung einer Sekante

Aufgabe 2

a) Wie ist eine Sekante,wie Sie sie im obigen Bild sehen können, definiert?

Text zum Verstecken

b) Berechnen Sie in diesem Applet die Steigung der Sekante durch die Punkte P und Q.

Text zum Verstecken

c) Stellen Sie die allgemeine Gleichung zur Berechnung der Steigung von Sekanten auf.

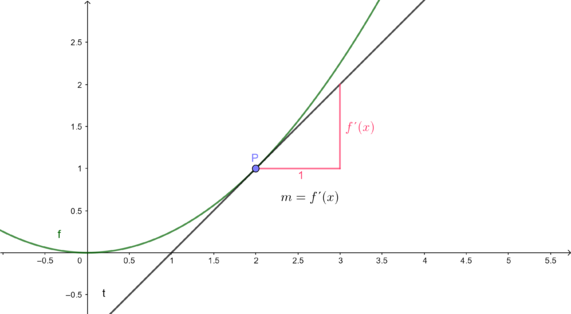
Die Steigung der Tangente

In dieser Aufgabe werden Sie sich die Berechnung der Steigung von Tangenten über den Differenzenquotienten herleiten.

Aufgabe 3

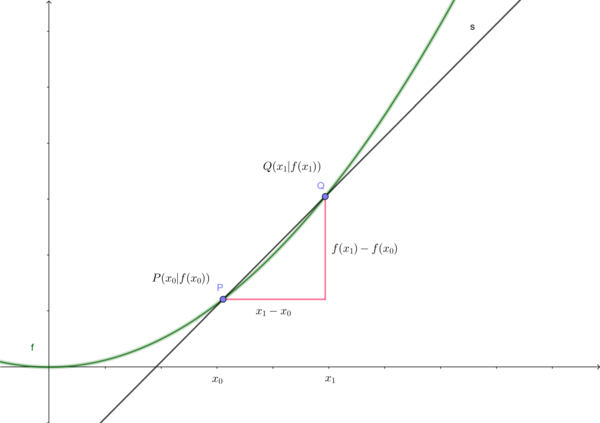
Wir betrachten die Funktion $f(x)=x^3+x$, den festen Punkt $P(x_0|f(x_0))$ mit $x_0=1$und den flexiblen Punkt $Q(x|f(x))$.
a) Nähern Sie den Punkt Q so nahe wie es das Applet zulässt dem Punkt P.
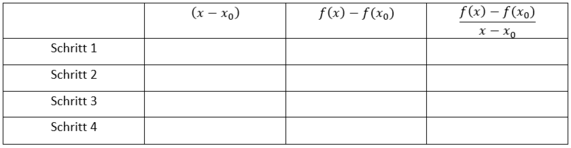
Tuen Sie dies indem Sie in 4 Schritten die Größe $x-x_0$ verkleinern.
Nutzen Sie hierfür die folgende Tabelle und entnehmen Sie die benötigten Werte dem Applet.

Zur Tabelle und zum Applet

b) Schätzen Sie in folgenden Applets durch Anlegen eines Stifts auf den Bildschirm die Steigung der Tangente im Punkt P.
Lassen Sie sich dann die Lösung anzeigen.

Applets anzeigen

c) Stellen Sie die allgemeine Gleichung zur Berechnung der Steigung von Sekanten auf.