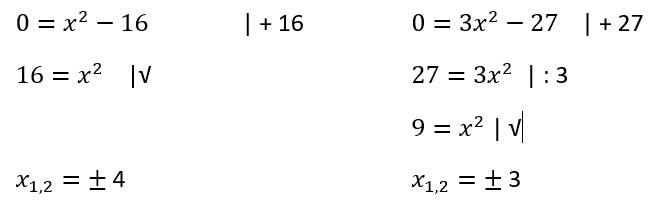Benutzer:Belli489/Nullstellen-quadratische-Funktionen

Nullstellen kommen in Anwendungsaufgaben zu quadratischen Funktionen sehr oft vor. Deshalb sollt du in den nächsten Stunden verschiedene Lösungsverfahren erarbeiten, mit denen man Nullstellen von quadratischen Funktionen berechnen kann. Dabei wirst du teils Musteraufgaben sehen, wie man Nullstellen berechnen kann, teils sollst du selbst erkennen, wie ein Verfahren funktioniert. Du kannst gerne mit einem Partner zusammenarbeiten.

Folgende Verfahren zur Bestimmung von Nullstellen wirst du kennen lernen:

• direktes Ausrechnen/ Wurzel ziehen
• Ausklammern
• p-q-Formel
• Ablesen aus der Linearfaktordarstellung

Nullstellen berechnen

Du solltest bereits aus der Einheit lineare Funktionen wissen, was man unter Nullstellen versteht.

Merke!

Nullstellen sind die Schnittpunkte mit der x-Achse!

Man berechnet die Nullstellen, indem man f(x)=0 setzt und die Gleichung nach x auflöst.

Denke also bei den folgenden Aufgaben stets daran, dass der erste Schritt immer sein muss, die Funktion =0 zu setzen!

Im Folgenden wirst du vier verschiedene Verfahren kennen lernen, um Nullstellen von quadratischen Funktionen zu berechnen:

1. Wurzel ziehen/ direktes Auflösen
2. Ausklammern
3. p-q-Formel
4. Ablesen aus der Linearfaktordarstellung

Möglichkeit 1: Direktes Ausrechnen/ Wurzel ziehen

Schauen wir uns zunächst einmal recht einfache quadratische Funktionen an:

Wichtig bei diesem Verfahren ist, dass du immer daran denkst, dass durch das Wurzelziehen sowohl die positive als auch die negative Zahl eine richtige Lösung ist!

Und nun: Übe das Verfahren!

Möglichkeit 2: Ausklammern

Betrachte die folgenden Funktionsgleichungen und zugehörigen Graphen:

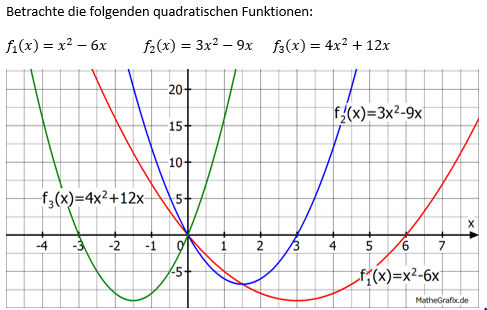
Beschreibe Gemeinsamkeiten bei der Funktionsgleichung und beim Graphen aller drei Funktionen: